| Autor |
Nachricht |
Quantenphysik
Gast
|
 Quantenphysik Verfasst am: 22. März 2018 10:06 Titel: Quantenzustand - Äquivalenzklasse Quantenphysik Verfasst am: 22. März 2018 10:06 Titel: Quantenzustand - Äquivalenzklasse |
 |
|
Hallo,
In Quantenmechanik-Büchern heißt es oft, dass Zustände als Elemente eines Hilbertraumes beschrieben werden.
Müsste es nicht mathematisch korrekter heißen, dass ein Zustand durch Äquivalenzklassen

beschrieben wird? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
 Myon Verfasst am: 22. März 2018 10:27 Titel: Myon Verfasst am: 22. März 2018 10:27 Titel: |
 |
|
|
Ja, es sind Äquivalenzklassen und (mit dieser Äquivalenzrelation wohl gleichbedeutend) eindimensionale Unterräume. Aber da können andere sicher kompetenter Auskunft geben. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 22. März 2018 12:27 Titel: TomS Verfasst am: 22. März 2018 12:27 Titel: |
 |
|
Ja, das ist formal richtig, jedoch für einfache praktische Anwendungen irrelevant bis hinderlich.
Es liegt dann kein Hilbertraum sondern ein sogenannter projektiver Hilbertraum mehr vor; d.h. insbs. dass eine Superposition von Zuständen nicht durch Summenbildung in diesem projektiven Hilbertraum erfolgt sondern weiterhin durch Summenbildung im zugrundeliegenden Hilbertraum
Man verwendet dies im Falle von verallgemeinerten Zuständen bzw. statistische Gemische, die mittels Dichteoperatoren beschrieben werden. Selbstverständlich kann man dies auch auf reine Zustände anwenden; der Dichteoperator zu einem Quantenzustand psi ist dann ein Projektor auf diesen eindimensionalen Unterraum
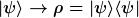
Falls man für das o.g. alpha

bzw.

fordert, ist die Äquivalenzrelation für den Dichteoperator sogar automatisch erfüllt, jedoch nicht für beliebiges alpha.
Ich für meinen Teil bin nie wirklich physikalischen Problemen begegnet, wo das wirklich wichtig gewesen wäre.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Quantenphysik
Gast
|
 Quantenphysik Verfasst am: 22. März 2018 13:38 Titel: Quantenphysik Verfasst am: 22. März 2018 13:38 Titel: |
 |
|
Demnach müssten doch nicht normierte Vektoren einer Äquivalenzklasse ebenso gute Repräsentanten sein wie deren normierte Vertreter.
Nur müsste dann das Postulat, dass sich die Messwahrscheinlichkeiten aus dem Betragsquadrat der Koeffizienten ergeben noch berücksichtigen, dass man durch die Norm der Vektoren teilt oder nicht?
Häufig lese ich nämlich, dass nur die normierten Vektoren einen Quantenzustand beschreiben, aber die nicht-normierten Zustände sollten dies auch tun, nur dass man bei den normierten Zuständen bei den Berechnungen (wie die Erwartungswerte) die Normierung der Wahrscheinlichkeiten nicht explizit berücksichtigen muss, weil dies implizit in der Normierung des Zustands bereits enthalten ist.
Somit hat man für einen Zustand zwei Freiheitsgrade (Realteil und Imaginärteil) und nicht nur einen Freiheitsgrad.
Bei fortgeschrittenen Themen ist es von essentieller Wichtigkeit, dass man Zustände nur bis auf einen Phasenfaktor bestimmen kann (z.B. wichtig in der QED). Genau genommen kann man aber doch den Zustand nur bis auf zwei Freiheitsgrade bestimmen oder liege ich damit falsch? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 22. März 2018 17:19 Titel: TomS Verfasst am: 22. März 2018 17:19 Titel: |
 |
|
Ja, nicht-normierte Repräsentanten sind ebenso zulässig. Die Normierung wandert vom Zustandsvektor in die Formeln zur Berechnung des Erwartungswertes etc.
Der Betrag oder Phasenfaktor eines Repräsentanten ist irrelevant; relevant bleiben jedoch relative Phasen zwischen verschiedenen Komponenten oder Rays. Am Beispiel der Dichteoperatoren
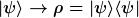

(\langle\psi_1|e^{-i\alpha} + \langle\psi_2|) \neq (|\psi_1\rangle + |\psi_2\rangle)(\langle\psi_1|+ \langle\psi_2|) )
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Quantenphysik
Gast
|
 Quantenphysik Verfasst am: 23. März 2018 22:48 Titel: Quantenphysik Verfasst am: 23. März 2018 22:48 Titel: |
 |
|
Hmm das Verhältnis der Beträge spielt aber auch eine Rolle, denn:
(\langle\psi_1|2 + \langle\psi_2|) \neq (|\psi_1\rangle + |\psi_2\rangle)(\langle\psi_1|+ \langle\psi_2|) ) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 24. März 2018 10:15 Titel: TomS Verfasst am: 24. März 2018 10:15 Titel: |
 |
|
Ja, das ist korrekt.
Es ging mir lediglich darum zu zeigen, dass relative Phase (oder Beträge) zwischen zwei Zustandsvektoren physikalisch relevant sind, dass jedoch globale Phasen oder Beträge irrelevant sind. Außerdem sieht man unmittelbar, dass die Rays keinen linearen Vektorraum definieren.
Übrigens ist die o.g. Formulierung noch unpräzise, denn wenn man auf die Äquivalenzklassen abzielt, dann gilt ja

Demzufolge müsste es in meinem o.g. Beispiel
(\langle\psi_1|e^{-ia} + \langle\psi_2|) \neq (|\psi_1\rangle + |\psi_2\rangle)(\langle\psi_1|+ \langle\psi_2|) )
eigtl. heißen:
(\langle\psi_1|e^{-ia} + \langle\psi_2|) \not\sim (|\psi_1\rangle + |\psi_2\rangle)(\langle\psi_1|+ \langle\psi_2|) )
D.h.
(\langle\psi_1|e^{-ia} + \langle\psi_2|) = \alpha (|\psi_1\rangle + |\psi_2\rangle)(\langle\psi_1|+ \langle\psi_2|) )
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Quantenphysik
Gast
|
 Quantenphysik Verfasst am: 24. März 2018 12:27 Titel: Quantenphysik Verfasst am: 24. März 2018 12:27 Titel: |
 |
|
Im Standardmodell der Teilchenphysik betrachtet man unitäre Transformationen und postuliert unter anderem eine lokale U(1)-Symmetrie.
In der gewöhnlichen Quantenmechanik liegt bereits eine globale U(1) Symmetrie vor. Darüber hinaus liegt nun aber auch eine globale Symmetrie bezüglich einer Multiplikation mit einem beliebigen komplexen Wert vor.
Meine Fragen sind nun.
Kann man die Forderung nach lokaler U(1) Eichsymmetrie motivieren außer dass dieser Ansatz zur richtigen Physik führt?
Müsste die Tatsache, dass in der Quantenmechanik die globale Symmetrie nicht nur bezüglich der Phasenfaktoren sondern auch bezüglich der Beträge besteht irgendwie Berücksichtigung finden? Folgt daraus aus dem Noether-Theorem eine weitere Erhaltungsgröße? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 24. März 2018 12:56 Titel: TomS Verfasst am: 24. März 2018 12:56 Titel: |
 |
|
| Quantenphysik hat Folgendes geschrieben: | Im Standardmodell der Teilchenphysik betrachtet man unitäre Transformationen und postuliert unter anderem eine lokale U(1)-Symmetrie.
In der gewöhnlichen Quantenmechanik liegt bereits eine globale U(1) Symmetrie vor. Darüber hinaus liegt nun aber auch eine globale Symmetrie bezüglich einer Multiplikation mit einem beliebigen komplexen Wert vor. |
Aus den lokalen Eichsymmetrien des klassischen Lagrangians folgen die zugehörigen erhaltenen Ladungen.
Aus der globalen U(1) Symmetrie der QM folgt mittels eines geeigneten Lagrangians die Schrödingergleichung sowie aus der Symmetrie des Lagrangians die Erhaltung der Wahrscheinlichkeit.
| Quantenphysik hat Folgendes geschrieben: | Kann man die Forderung nach lokaler U(1) Eichsymmetrie motivieren außer dass dieser Ansatz zur richtigen Physik führt?
|
M.E. kann man dies nicht ohne Bezugnahme auf die Stringtheorie.
| Quantenphysik hat Folgendes geschrieben: | | Müsste die Tatsache, dass in der Quantenmechanik die globale Symmetrie nicht nur bezüglich der Phasenfaktoren sondern auch bezüglich der Beträge besteht irgendwie Berücksichtigung finden? Folgt daraus aus dem Noether-Theorem eine weitere Erhaltungsgröße? |
Dazu müsstest du eine Lagrangedichte finden, die die Gruppe GL(1,C) als Symmetriegruppe hat und aus der die Schrödingergleichung bzw. eine äquivalente Gleichung für Rays folgt. Ich kenne keine derartige Lagrangedichte; deine Frage ist für mich völlig neu.
(beachte, dass Dichteoperatoren nicht ausreichen, denn für diese liegt nur die benannte U(1) Symmetrie vor). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 24. März 2018 13:30 Titel: TomS Verfasst am: 24. März 2018 13:30 Titel: |
 |
|
Evtl. Führt das auch etwas in die Irre.
In der nicht-rel. QM folgt die Erhaltung der Wahrscheinlichkeit aus der Lagrangedichte
 - \psi^\ast\psi V)
Es sieht nun so aus, als wäre diese eine gewöhnliche Lagrangedichte wie in einer Feldtheorie.
Tatsächlich handelt es sich lediglich um eine sehr spezielle Darstellung, nämlich die Ortsdarstellung, aus der die Schrödingergleichung für die Wellenfunktion
 = \langle x|\psi\rangle )
folgt.
Tatsächlich fundamental ist die darstellungsfreie Schrödingergleichung für den Zustandsvektor

Diese Form ist universell und gilt auch - obwohl kaum gebräuchlich - in der Quantenfeldtheorie.
In letzterer existiert jedoch m.W.n. keine sinnvolle "Lagrangedichte" zur Herleitung dieser Schrödingergleichung. Die Lagrangedichten sind hier immer klassische Objekte, aus denen der Hamiltonian H sowie die klassischen Symmetrien und erhaltenen Ladungen, ausgedrückt durch die Feldoperatoren gewonnen werden.
Die globale U(1) Symmetrie der Schrödingergleichung gilt ausschließlich für den Zustandsvektor, d.h. sie ist trivial = entspricht der Eins für die Quantenfelder, während die weiteren Symmetrien aus den bekannten Feldtheorien für die Quantenfelder und den Zustandsvektor gelten.
Ich halte die o.g. Lagrangedichte für die Schrödingergleichung eher für zufälligerweise im Rahmen der nicht-rel. QM für richtig, nicht für universell sinnvoll.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 24. März 2018 14:51, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 24. März 2018 14:18 Titel: TomS Verfasst am: 24. März 2018 14:18 Titel: |
 |
|
Nochmal anders betrachtet, nämlich im Heisenbergbild.
Beachte: im Heisenbergbild sind die Zustände zeitunabhängig; die Zeitabhängigkeit steckt in den Operatoren A gemäß der Heisenberggleichung
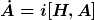
Betrachten wir eine allgemeine unitäre Transformation


mit einem selbstadjungierten Generator Q und reellem Parameter theta.
Jedes beliebige quantenmechanische Modell ist invariant unter beliebigen derartigen unitäre Transformation.
Für den Spezialfall, dass
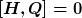
gilt, folgt einerseits, dass

d.h. Q ist eine Symmetrie von H;
es folgt andererseits, dass

d.h. Q ist erhalten.
Dies ist letztlich die quantenmechanische Variante des Noethertheorems, demzufolge Symmetrien des Systems bzw. des Hamiltonians erhaltenen Ladungen entsprechen u.u.
Das klassische Noethertheorem hilft, die Qs zu konstruieren; die Implementierung als unitäre Transformation geht über das klassische Noethertheorem hinaus.
Betrachten wir die Invarianz unter der speziellen U(1) Symmetrie

Hier ist trivialerweise



D.h. es handelt es sich um eine Symmetrie mit dem Generator Q = 1, also dem Identitätsoperator. Dieser existiert trivialerweise für jede beliebige Theorie und hat keine physikalische Relevanz.
Betrachten wir desweiteren eine beliebige Transformation mit einem Generator Q, der nicht mit dem Hamiltonian H vertauscht, d.h. der keiner Symmetrie des Systems entspricht. Dieses Q folgt demnach nicht aus der Anwendung des Noethertheorems.
Anderseits liegt tatsächlich eine Symmetrie vor, in dem Sinne dass die unitäre Transformation z.B. Erwartungswerte invariant lässt, allerdings eben nicht H alleine. Diese Art der Symmetrie unter beliebigen unitären Transformationen ist also allgemeiner und folgt nicht aus dem Noethertheorem.
Anmerkung zur Quantenfeldtheorie: auch hier liegt eine Variante des quantenmechanischen Noethertheorems vor. Betrachten wir dazu die klassische Elektrodynamik mit dem Gaußschen Gesetz
 = \nabla E - \rho = 0)
In der QED wird daraus eine Gleichung, die nicht für Operatoren sondern lediglich für Zustände den physikalischen Unterraums eines größeren kinematischen Hilbertraumes gilt:
 \, |\text{phys}\rangle = 0)
Es gilt übrigens
] = 0)
d.h. das Gaußsche Gesetz entspricht einer lokalen Symmetrie der QED.
Daraus konstruiert man unendlich viele erhaltene Ladungen
 \, \theta(x) )
mittels beliebiger Funktionen theta.
Diese unendlich vielen erhaltenen Ladungen sind im o.g. Sinne Generatoren unendlich vieler Symmetrien, nämlich der lokalen Eichsymmetrie mit Eichfunktion theta.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|












