| Autor |
Nachricht |
Dr.Stupid
Gast
|
 Dr.Stupid Verfasst am: 01. Apr 2015 20:52 Titel: Kets und Bras Dr.Stupid Verfasst am: 01. Apr 2015 20:52 Titel: Kets und Bras |
 |
|
Hallo.
Ich habe ein Verständnisproblem. Ich habe im QM1-Buch von Tannoudji gelesen, dass es zu jedem Ket einen Bra gibt, aber nicht zu jedem Bra einen Ket. Die Erklärung im Tannoudji habe ich jedoch nicht verstanden. Kann mir jemand evtl. mit eigenen Worten erklären, warum dies so ist?
Viele Grüße |
|
 |
Nobundo
Anmeldungsdatum: 12.03.2014
Beiträge: 168
|
 Nobundo Verfasst am: 01. Apr 2015 21:27 Titel: Nobundo Verfasst am: 01. Apr 2015 21:27 Titel: |
 |
|
Ich glaube das hängt damit zusammen, dass man mit "kets" die Elemente eines Vektorraums V bezeichnet, während die "Bra's" Elemente des Dualraumes V* sind.
Um beide miteinander 1:1 zu identifizieren benutzt man meistens ein Skalarprodukt oder allgemeiner eine nicht ausgeartete symmetrische (bzw. hermitesche) Bilineare Abbildung VxV-> R (bzw C).
Ohne eine solche Abbildung ist eine Identifizierung i.A. nicht möglich, vielleicht kann ich genaueres sagen, wenn du mehr informationen angibst in welchem mathematischen Rahmen du die Frge stellst.
Gruß
Nobundo |
|
 |
Dr.Stupid
Gast
|
 Dr.Stupid Verfasst am: 01. Apr 2015 22:05 Titel: Dr.Stupid Verfasst am: 01. Apr 2015 22:05 Titel: |
 |
|
Danke für deine antwort, ich bin mir aber nicht sicher ob ich diese verstehe.
Zum Skalarprodukt: Man kann ja jedem Ket ein lineares Funktional (den Bra) zuordnen, indem man einfach über das skalarprodukt von ket und bra jedem ket eine (komplexe) Zahl zuordnet.
Ich verstehe nun nicht, warum dies nciht analog für den Bra möglcih ist, indem ich jedem Bra über das Skalarprodukt ein lineares Funktional (den Ket) zuordne. Es kommt mir komisch vor, dass der Hilbertraum (für die Kets) und der duale Hilbertraum (für die Bras) in dem Sinne nicht gleichberechtigt sind.
Ich hoffe ich konnte damit meine frage etwas präzisieren. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 02. Apr 2015 00:25 Titel: Jayk Verfasst am: 02. Apr 2015 00:25 Titel: |
 |
|
Erstmal: Im Gegensatz zu allgemeinen Banachräumen sind Hilberträume immer zu ihren topologischen Dualräumen kanonisch isomorph (Rieszscher Darstellungssatz). Für endlich-dimensionale Vektorräume ist das sowieso immer der Fall, aber für unendlichdimensionale Banachräume ist der Bidualraum im Allgemeinen größer. Doch bei Hilberträumen eben nicht.
Das Problem, das im Buch vermutlich angesprochen wird, ist die Unterscheidung zwischen topologischem und algebraischem Dualraum (für endlichdimensionale Vektorräume sind beide Begriffe äquivalent). Der algebraische Dualraum V* besteht aus allen linearen Funktionalen, der topologische Dualraum V' aus allen stetigen (= beschränkten) linearen Funktionalen. (wenn man einfach von "Dualraum" spricht, ist eigentlich immer der topologische Dualraum gemeint)
Nun dachte ich eigentlich bisher, dass man unter einem 'Bra' ein beschränktes lineares Funktional versteht. Anscheinend ist das wohl nicht der Fall.
EDIT: http://de.wikipedia.org/wiki/Rieszscher_Darstellungssatz#Der_Satz_von_Fr.C3.A9chet-Riesz
Noch eine Anmerkung: Ich finde den Satz nicht trivial. Ich vermute, dass der Grund, weshalb dir eine vermeintliche Ungleichheit komisch vorkommt, in der suggestiven Bra-Ket-Notation liegt, die nicht zwischen Paarung von Vektoren und Kovektoren und Skalarproduktbildung unterscheidet. Durch den Rieszschen Darstellungssatz wird sie meines Erachtens nach erst gerechtfertigt. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 02. Apr 2015 08:57 Titel: TomS Verfasst am: 02. Apr 2015 08:57 Titel: |
 |
|
Ich denke, wichtig ist zunächst mal, dass man im Hinterkopf behält, dass die Identifizierung von Raum und Dualraum im Falle unendlich-dimensionaler Vektorräume weiterer Voraussetzungen bedarf.
Man muss unterscheiden zwischen der Zuordnung eines Bras aus H* zu einem Ket aus H

und der umgekehrten Zuordnung. Die o.g. Zuordnung funktioniert natürlich immer, die umgekehrte eben nicht.
Definiert man den Dualraum im Sinne von Jayk, dann ist i.A.

d.h. nicht alle linearen Funktionale aus H* entsprechen auch Zustände aus H.
Ein Beispiel:

\,v(x))
Natürlich können u und v beide aus L2 sein. Allerdings ist ja bekanntermaßen auch
\,v(x) = v(x_0))
eine gültige Abbildung, d.h. die Delta-Distribution definiert ein gültiges lineares Funktional auf dem Raum der quadratintegrablen Funktionen, ohne jedoch selbst quadratintegrabel zu sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Dr.Stupid
Gast
|
 Dr.Stupid Verfasst am: 02. Apr 2015 11:38 Titel: Dr.Stupid Verfasst am: 02. Apr 2015 11:38 Titel: |
 |
|
Danke euch beiden für eure antworten. V.a. das Beispiel von Toms war sehr hilfreich  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 02. Apr 2015 13:33 Titel: jh8979 Verfasst am: 02. Apr 2015 13:33 Titel: |
 |
|
|
[Kleine Mod-Anmerkung: Da wir einen durchaus aktiven Nutzer namens DrStupid haben, wäre es vermutlich ganz nett, wenn Du nächstes mal einen anderen Gastnamen verwendest, nur um Verwechselungen vorzubeugen...] |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Apr 2015 16:18 Titel: index_razor Verfasst am: 02. Apr 2015 16:18 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Ich denke, wichtig ist zunächst mal, dass man im Hinterkopf behält, dass die Identifizierung von Raum und Dualraum im Falle unendlich-dimensionaler Vektorräume weiterer Voraussetzungen bedarf.
Man muss unterscheiden zwischen der Zuordnung eines Bras aus H* zu einem Ket aus H

und der umgekehrten Zuordnung. Die o.g. Zuordnung funktioniert natürlich immer, die umgekehrte eben nicht.
|
In einem Hilbertraum schon. Siehe den von Jayk zitierten Rieszschen Darstellungssatz. Zu deinem Gegenbeispiel siehe unten.
| Zitat: |
Definiert man den Dualraum im Sinne von Jayk, dann ist i.A.

d.h. nicht alle linearen Funktionale aus H* entsprechen auch Zustände aus H.
|
Nun, das ist etwas unglücklich ausgedrückt. Denn der Vektorraum ist natürlich keine Teilmenge seines Dualraums, unabhängig von der Frage ob beide isomorph sind.
| Zitat: |
Ein Beispiel:

\,v(x))
Natürlich können u und v beide aus L2 sein. Allerdings ist ja bekanntermaßen auch
\,v(x) = v(x_0))
eine gültige Abbildung, d.h. die Delta-Distribution definiert ein gültiges lineares Funktional auf dem Raum der quadratintegrablen Funktionen, ohne jedoch selbst quadratintegrabel zu sein. |
Das kann man so nicht sagen. Die Menge der quadratintegrablen Funktionen bildet keinen Hilbertraum, nicht mal einen normierten Raum, da aus

nicht  folgt, sondern nur folgt, sondern nur  fast überall. Aus diesem Grund betrachtet man nicht die Menge der quadratintegrablen Funktionen selbst (die ist zu sozusagen zu groß), sondern die Äquivalenzklassen fast überall. Aus diesem Grund betrachtet man nicht die Menge der quadratintegrablen Funktionen selbst (die ist zu sozusagen zu groß), sondern die Äquivalenzklassen

d.h. ein Hilbertraumvektor ist die Menge der Funktionen, die sich höchstens auf einer Nullmenge voneinander unterscheiden. Auf diesen Äquivalenzklassen ist aber die ) -Distribution nicht definiert, da eine Äquivalenzklasse keinen definierten Funktionswert an der Stelle -Distribution nicht definiert, da eine Äquivalenzklasse keinen definierten Funktionswert an der Stelle 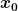 besitzt. besitzt. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 02. Apr 2015 17:04 Titel: Jayk Verfasst am: 02. Apr 2015 17:04 Titel: |
 |
|
@index_dazor: Was du zu  = \mathcal{L}^2 (M, dx) / \sim) gesagt hast, habe ich mir auch erst gedacht, aber das Beispiel von TomS funktioniert meiner Meinung nach trotzdem, wenn man gesagt hast, habe ich mir auch erst gedacht, aber das Beispiel von TomS funktioniert meiner Meinung nach trotzdem, wenn man
\,dx)
definiert: Jeder der Integrationsbereiche hat ein endliches Maß, die Integrale sind unabhängig vom Repräsentanten. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 02. Apr 2015 18:05 Titel: Jayk Verfasst am: 02. Apr 2015 18:05 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Natürlich können u und v beide aus L2 sein. Allerdings ist ja bekanntermaßen auch
\,v(x) = v(x_0))
eine gültige Abbildung, d.h. die Delta-Distribution definiert ein gültiges lineares Funktional auf dem Raum der quadratintegrablen Funktionen |
Jetzt muss ich allerdings über die Formulierung "bekanntermaßen" schmunzeln.  Zum Beispiel ist Zum Beispiel ist  = \vert x \vert^{-1/3} \chi_{[-1,1]}(x)) eine L²-Funktion. Sie hat aber eine Singularität, somit wäre eine L²-Funktion. Sie hat aber eine Singularität, somit wäre  . Lineare Funktionale müssen aber nach . Lineare Funktionale müssen aber nach  abbilden. Durch abbilden. Durch  wird also kein lineares Funktional definiert. wird also kein lineares Funktional definiert.
Damit bleibt die Frage, ob der algebraische Dualraum irgendeine Relevanz für die QM hat. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Apr 2015 19:21 Titel: index_razor Verfasst am: 02. Apr 2015 19:21 Titel: |
 |
|
@Jayk, ok, TomS sprach nur von einem "linearen" Funktional. Ich hatte an die Menge stetiger linearer Funktionale gedacht, weil das auf topologischen Vektorräumen die natürliche Definition von Dualraum ist. Das von dir definierte Funktional ist ja auch nicht beschränkt, man kann z.B. eine Folge  wählen mit wählen mit

(für hinreichend kleines  ) und ) und  fast überall. Das heißt also fast überall. Das heißt also  , aber , aber  . .
Allerdings bleibt die Behauptung
| TomS hat Folgendes geschrieben: | Allerdings ist ja bekanntermaßen auch
\,v(x) = v(x_0))
eine gültige Abbildung, d.h. die Delta-Distribution definiert ein gültiges lineares Funktional auf dem Raum der quadratintegrablen Funktionen, ohne jedoch selbst quadratintegrabel zu sein. |
m.E. falsch. ) ist kein gültiges lineares Funktional auf ist kein gültiges lineares Funktional auf  . . |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 02. Apr 2015 21:31 Titel: Jayk Verfasst am: 02. Apr 2015 21:31 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | @Jayk, ok, TomS sprach nur von einem "linearen" Funktional. Ich hatte an die Menge stetiger linearer Funktionale gedacht, weil das auf topologischen Vektorräumen die natürliche Definition von Dualraum ist. |
Ja, das habe ich ja auch schon weiter oben geschrieben. 
Aber ein lineares Funktional ist es trotzdem nicht (ein stetiges sowieso nicht). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 02. Apr 2015 22:01 Titel: TomS Verfasst am: 02. Apr 2015 22:01 Titel: |
 |
|
Sorry, ich war nicht exakt genug.
Man benötigt Gelfandsche Tripel. Damit ist die Delta-Distribution ein lineares Funktional, allerdings nicht auf dem L2 selbst sondern auf einem Schwarz-Raum. Und in dem Sunne ist auch die Untermenge zu verstehen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 03. Apr 2015 00:40 Titel: Jayk Verfasst am: 03. Apr 2015 00:40 Titel: |
 |
|
@TomS: Ich verstehe nicht, was du damit sagen willst. Dass die Delta-Distribution eine temperierte Distribution ist, weiß ich. Und dass der Schwartz-Raum  dicht in dicht in  ist, weiß ich auch. Aber das macht eine temperierte Distribution doch nicht zu einem Funktional auf L²... ist, weiß ich auch. Aber das macht eine temperierte Distribution doch nicht zu einem Funktional auf L²...
Welche Untermenge meinst du? Dass  gilt, ist auch klar. Aber das ist ja auch ein lokalkonvexer Raum und kein Hilbertraum... gilt, ist auch klar. Aber das ist ja auch ein lokalkonvexer Raum und kein Hilbertraum... |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Apr 2015 06:55 Titel: index_razor Verfasst am: 03. Apr 2015 06:55 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | @Jayk, ok, TomS sprach nur von einem "linearen" Funktional. Ich hatte an die Menge stetiger linearer Funktionale gedacht, weil das auf topologischen Vektorräumen die natürliche Definition von Dualraum ist. |
Ja, das habe ich ja auch schon weiter oben geschrieben. 
|
Ja, habe ich dann auch gemerkt. ;-) Mir war "topologischer Dualraum" nicht geläufig, obwohl es eine passende Bezeichnung ist und ich hatte nicht weiter drüber nachgedacht, was du damit meinst.
(EDIT: oh, du definierst ihn sogar. Kein Ahnung wie ich das übersehen konnte, sorry.)
| Zitat: |
Aber ein lineares Funktional ist es trotzdem nicht (ein stetiges sowieso nicht). |
Welches meinst du jetzt? Das, sagen wir mal "übliche"  ist linear und stetig auf dem Testfunktionenraum. Der ist aber kein Banachraum bzgl. der L²-Norm, also auch kein Hilbertraum. ist linear und stetig auf dem Testfunktionenraum. Der ist aber kein Banachraum bzgl. der L²-Norm, also auch kein Hilbertraum.
Testfunktionen, zusammen mit deren Vervollständigung bzgl. der L²-Norm und ihrem Dualraum bilden, wenn ich mich richtig erinnere, das Gelfand-Raumtripel was TomS erwähnt hat. Der Dualraum ist hier sozusagen "größer" als der Testfunktionenraum (in dem Sinne, das beide nicht wie im Hilbertraumfall isometrisch isomorph sind), weil der Rieszsche Darstellungssatz nicht anwendbar ist (er benötigt ausdrücklich die Vollständigkeit). Du kannst nun  als lineares Funktional auf L² auffassen -- du hast ja selbst eine mögliche Definition genannt -- nur eben nicht als stetiges und damit nicht als ein Element aus dem L²-Dual. (EDIT: bzw. um bei der oben eingeführten Sprechweise zu bleiben: Es wäre ein Element aus dem algebraischen Dualraum von L² aber nicht aus dem topologischen Dualraum.) als lineares Funktional auf L² auffassen -- du hast ja selbst eine mögliche Definition genannt -- nur eben nicht als stetiges und damit nicht als ein Element aus dem L²-Dual. (EDIT: bzw. um bei der oben eingeführten Sprechweise zu bleiben: Es wäre ein Element aus dem algebraischen Dualraum von L² aber nicht aus dem topologischen Dualraum.) |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 03. Apr 2015 09:56 Titel: Jayk Verfasst am: 03. Apr 2015 09:56 Titel: |
 |
|
Aber was ist mit der genannten Funktion  = \vert x \vert^{-1/3} \chi_{[-1,1]}(x)) , , ) ? Die definiert eine L²-Funktion, aber definitiv keine Schwartz-Funktion auf R (sie ist ja nicht glatt). Aber ? Die definiert eine L²-Funktion, aber definitiv keine Schwartz-Funktion auf R (sie ist ja nicht glatt). Aber  \to \mathbb C) ist stetig bezüglich der durch die Normen ist stetig bezüglich der durch die Normen ^{m} \vert D^\alpha f(x) \vert) definierten Schwach*-Topologie, deswegen braucht es ja nicht stetig bezüglich der L²-Norm zu sein. Daher muss es auch keine Fortsetzung haben, denn L² ist ja, wie du gesagt hast, die Fortsetzung von S bezüglich der L²-Norm, bezüglich seiner eigenen Topologie ist S ja selber vollständig. definierten Schwach*-Topologie, deswegen braucht es ja nicht stetig bezüglich der L²-Norm zu sein. Daher muss es auch keine Fortsetzung haben, denn L² ist ja, wie du gesagt hast, die Fortsetzung von S bezüglich der L²-Norm, bezüglich seiner eigenen Topologie ist S ja selber vollständig.
Welchen Wert hätte also delta, ausgewertet bei obiger L²-Testfunktion? Als Funktional müsste es ja nach  abbilden, also kommt abbilden, also kommt 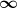 als Wert nicht infrage. als Wert nicht infrage.
(das Problem mit der Definition, die ich genannt habe, ist, dass nicht garantiert ist, dass der Limes der Integrale existiert)
Es gilt ja  (die Teilmengen sind dicht), folglich gilt auch umgekehrt (die Teilmengen sind dicht), folglich gilt auch umgekehrt ' = L^2 \subset \mathcal S') . Es gilt aber weder . Es gilt aber weder  , noch , noch  . . |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Apr 2015 13:14 Titel: index_razor Verfasst am: 03. Apr 2015 13:14 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: | Aber was ist mit der genannten Funktion  = \vert x \vert^{-1/3} \chi_{[-1,1]}(x)) , , ) ? ?
[...]
Welchen Wert hätte also delta, ausgewertet bei obiger L²-Testfunktion? Als Funktional müsste es ja nach  abbilden, also kommt abbilden, also kommt 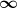 als Wert nicht infrage. als Wert nicht infrage.
(das Problem mit der Definition, die ich genannt habe, ist, dass nicht garantiert ist, dass der Limes der Integrale existiert)
|
Ich denke es ist gängig, wenn auch irgendwie fragwürdig, von unbeschränkten Abbildungen nur zu verlangen, dicht definiert zu sein. (Der Grund ist vielleicht, daß es für die Anwendungen immer egal ist, auf welchem dichten Teilraum das Funktional definiert ist.) Streng genommen hast du, denke ich, absolut recht  ist nicht auf ganz L² definiert. Darüber, daß es nicht stetig bzgl. der L²-Norm ist, waren wir uns ja sowieso schon einig. ist nicht auf ganz L² definiert. Darüber, daß es nicht stetig bzgl. der L²-Norm ist, waren wir uns ja sowieso schon einig.
(Ansonsten denke ich, wir reden hier etwas aneinander vorbei. Mit Testfunktionen meinte ich glatte Funktionen mit kompaktem Träger (Schwartzsche Fuktionen gehen stattdessen aber wohl auch), also auf jeden Fall nicht die Funktion f.) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 03. Apr 2015 23:11 Titel: TomS Verfasst am: 03. Apr 2015 23:11 Titel: |
 |
|
Irgendwie verstehe ich meine eigene Idee nicht mehr :-(
Ich fasse mal ein paar Gedanken zusammen, und hoffe, ihr könnt mir ein paar weitere Hinweise geben.
Gemäß der Axiome der QM formulieren wir diese in einem separablen Hilbertraum; ein Beispiel ist der L2 über R. Allerdings ist dieser für viele praktische Anwendungen "zu klein"; so kann man im L2[R] die Observablen x und p nicht diskutieren, da diese in diesem Raum nicht selbstajungiert sind; als solche müssten sie einen vollständigen Satz von Eigenfunktionen in L2[R] haben; die "verallgemeinerten Eigenfunktionen" sind jedoch nicht Elemente von L2[R], da nicht quadratintegrabel. Daraus folgt, dass man den Abschluss von L2[R] betrachten muss, um x und p vernünftig diskutieren zu können.
Bis hierher reden wir nicht vom Dualraum sondern vom Abschluss eines Raumes. Ich dachte nun, dass der Abschluss ebenfalls als Hilbertraum (im Sinne der Konstruktion der rigged Hilbert spaces bzw. Gelfand triples) aufgefasst werden kann. Damit sind wir aber unmittelbar beim Dualraum als Raum linearer Funktionale.
Mir ist nicht ganz klar, welche Bedingungen diese Funktionale genau erfüllen müssen. Insbs. denke ich aber, das man mit der o.g. Konstruktion auch zulassen muss, dass diese Funktionale nicht mehr nach C sondern in den Abschluss von C einschließlich Unendlich abbilden (genauso wie im Abschluss von L2 nicht-normierbare Funktionen enthalten sind).
Demnach würde ich zunächst behaupten, dass der Dualraum L2*[R] zu L2[R] exakt wieder der L2*[R] ist, d.h. es liegt Selbst-Dualität vor. Lasse ich nun einige Einschränkungen für die linearen Funktionale fallen, so sind die Distributionen im Sinne eines Schwarz-Raumes zulässig. Und damit dachte ich, dass dies auch für den Abschluss gelten müsse, d.h. dass der Dualraum des Abschlusses wieder auf den Abschluss führt.
Gilt das? Ich kenne den Beweis für L2, nicht jedoch für den Abschluss.
Nun ein weiterer Punkt, den ich nicht mehr verstehe: wenn man sich auf den L2[R] beschränkt, ist zunächst L2*[R] = L2[R] und die eingangs zitierte Feststellung bzgl. der Bras und Kets ist falsch; wenn meine hier diskutierte Idee richtig ist, dann gilt dies auch für den Abschluss, und sowohl die eingangs zitierte Feststellung sowie mein Beispiel sind falsch (wiederum wäre der Dualraum mit Raum identisch).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 04. Apr 2015 00:08 Titel: Jayk Verfasst am: 04. Apr 2015 00:08 Titel: |
 |
|
@TomS: Hm, also wenn selbst du verwirrt bist...^^
Also zunächst mal ist jeder topologische Raum bezüglich seiner eigenen Topologie per definitionem abgeschlossen. Wenn ich also einen Raum abschließe, dann bezüglich einer anderen Topologie (und das Ergebnis hängt dann selbstverständlich davon ab, welche Topologie ich dafür verwende). Nun ist  , Abschluss bezüglich der S'-Topologie. , Abschluss bezüglich der S'-Topologie.  ist aber definitiv kein Hilbertraum. Der Raum ist aber definitiv kein Hilbertraum. Der Raum  der Schwartzfunktionen ist zwar metrisierbar, aber nicht normierbar. (Außerdem gibt es ja genügend Beispiele für temperierte Distributionen, die nicht regulär sind, wie die Delta-Distribution) der Schwartzfunktionen ist zwar metrisierbar, aber nicht normierbar. (Außerdem gibt es ja genügend Beispiele für temperierte Distributionen, die nicht regulär sind, wie die Delta-Distribution)
| TomS hat Folgendes geschrieben: | | Ich dachte nun, dass der Abschluss ebenfalls als Hilbertraum (im Sinne der Konstruktion der rigged Hilbert spaces bzw. Gelfand triples) aufgefasst werden kann. |
Könnte es möglicherweise sein, dass du das gerade damit verwechselst, dass jeder Prähilbertraum eindeutig (bis auf isometrische Isomorphie) zu einem Hilbertraum fortgesetzt werden kann, der von diesem das Skalarprodukt erbt?
| TomS hat Folgendes geschrieben: | | Und damit dachte ich, dass dies auch für den Abschluss gelten müsse, d.h. dass der Dualraum des Abschlusses wieder auf den Abschluss führt. |
Ich bin mir nicht sicher, ob ich verstehe, was du meinst. Meinst du, dass aus  folgen soll, dass folgen soll, dass  ? Das kann schon prinzipiell nicht richtig sein, weil der Dualraum eines größeren Raumes kleiner als der Dualraum des kleineren Raumes sein muss. Es muss ja dann jedes Funktional mehr Elemente in den Körper abbilden und da wird es natürlich ein paar geben, die ausscheiden, weil sie nicht für alle neu dazugekommenen Elemente wohldefiniert sind (wie wir ja gerade an einem Beispiel gesehen haben). ? Das kann schon prinzipiell nicht richtig sein, weil der Dualraum eines größeren Raumes kleiner als der Dualraum des kleineren Raumes sein muss. Es muss ja dann jedes Funktional mehr Elemente in den Körper abbilden und da wird es natürlich ein paar geben, die ausscheiden, weil sie nicht für alle neu dazugekommenen Elemente wohldefiniert sind (wie wir ja gerade an einem Beispiel gesehen haben). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 04. Apr 2015 16:18 Titel: TomS Verfasst am: 04. Apr 2015 16:18 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: | | Wenn ich also einen Raum abschließe, dann bezüglich einer anderen Topologie (und das Ergebnis hängt dann selbstverständlich davon ab, welche Topologie ich dafür verwende). |
Das ist klar.
| Jayk hat Folgendes geschrieben: | Nun ist  , Abschluss bezüglich der S'-Topologie. , Abschluss bezüglich der S'-Topologie.  ist aber definitiv kein Hilbertraum. Der Raum ist aber definitiv kein Hilbertraum. Der Raum  der Schwartzfunktionen ist zwar metrisierbar, aber nicht normierbar. der Schwartzfunktionen ist zwar metrisierbar, aber nicht normierbar. |
Auch das ist bzgl. S zunächst klar.
Und du sagst darüberhinaus, dass von S aus kein Weg zu einem größeren Hilbertraum führt.
| Jayk hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Ich dachte nun, dass der Abschluss ebenfalls als Hilbertraum (im Sinne der Konstruktion der rigged Hilbert spaces bzw. Gelfand triples) aufgefasst werden kann. |
Könnte es möglicherweise sein, dass du das gerade damit verwechselst, dass jeder Prähilbertraum eindeutig (bis auf isometrische Isomorphie) zu einem Hilbertraum fortgesetzt werden kann, der von diesem das Skalarprodukt erbt? |
Nein, das war nicht meine Idee.
| Jayk hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Und damit dachte ich, dass dies auch für den Abschluss gelten müsse, d.h. dass der Dualraum des Abschlusses wieder auf den Abschluss führt. |
Ich bin mir nicht sicher, ob ich verstehe, was du meinst. Meinst du, dass aus  folgen soll, dass folgen soll, dass  ? ? |
Genau das meine ich. Ist der Dualraum des Abschlusses identisch mit dem Abschluss des Dualraumes.
| Jayk hat Folgendes geschrieben: | | WennDas kann schon prinzipiell nicht richtig sein, weil der Dualraum eines größeren Raumes kleiner als der Dualraum des kleineren Raumes sein muss. Es muss ja dann jedes Funktional mehr Elemente in den Körper abbilden und da wird es natürlich ein paar geben, die ausscheiden, weil sie nicht für alle neu dazugekommenen Elemente wohldefiniert sind (wie wir ja gerade an einem Beispiel gesehen haben). |
Und selbst wenn, dann hilft das im vorliegenden Fall nicht weiter, da kein Hilbertraum vorliegt.
Ich versuche, den Sinn der ursprünglichen Frage zu verstehen. Und je mehr ich darüber nachdenke, desto mehr komme ich zu der Erkenntnis, dass dieses Statement zu vage ist, um etwas sinnvolles dazu sagen zu können.
Im Sinne des  wissen wir sicher, dass es falsch ist, denn es ist wissen wir sicher, dass es falsch ist, denn es ist
^\ast = L^2[\mathbb{R}])
Im Sinne des Abschlusses  wissen wir, dass kein Hilbertraum vorliegt, d.h. dass wir streng genommen die axiomatische Basis der Quantenmechanik verlassen. wissen wir, dass kein Hilbertraum vorliegt, d.h. dass wir streng genommen die axiomatische Basis der Quantenmechanik verlassen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 04. Apr 2015 19:36 Titel: TomS Verfasst am: 04. Apr 2015 19:36 Titel: |
 |
|
Es gilt doch

d.h. der topologische Dualraum zu S ist der Raum der temperierten Distributionen S'. In diesem Sinne könnte die Bemerkung zu verstehen sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 04. Apr 2015 20:09 Titel: Jayk Verfasst am: 04. Apr 2015 20:09 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Und du sagst darüberhinaus, dass von S aus kein Weg zu einem größeren Hilbertraum führt. |
Nein. Ich sage nur, dass S und somit auch S' kein Hilbertraum ist. 
Meinst du in obigem Zitat S oder S'? Denn L² ist ja ein größerer Hilbertraum als S. Aber einen größeren Hilbertraum als S' kenne ich jedenfalls nicht. Das heißt ja nicht, dass es keinen gibt.
Ich denke allerdings, die ursprüngliche Fragestellung haben wir fast geklärt: Ich habe mir die Argumentation im Cohen-Tannoudji durchgelesen. Besonders lehrreich war sie nicht. Um es so zusammenzufassen: Mit Dualraum ist dort der algebraische Dualraum gemeint, d.h. Bras sind lineare Funktionale, müssen also nicht notwendig stetig sein. Es werden zwei Beispiele gebracht, eines davon ist die Delta-Distribution.
Wen es interessiert: http://www.dfi.uchile.cl/~paurruti/Cuantica%20II/Physics%20-%20Quantum%20Mechanics,%20Vol%201%20-%20Cohen%20-%20Tannoudji.pdf, ab Seite 111.
Ich weiß nicht, wozu die Diskussion im Buch gut sein soll. Dort wird immer so vorgegangen, dass man den Limes von stetigen Bras nimmt und dann feststellt, dass es dazu keinen Bra gibt.
Beim zweiten Beispiel habe ich nicht überprüft, ob das entstandene Funktional wohldefiniert ist. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 04. Apr 2015 20:28 Titel: Jayk Verfasst am: 04. Apr 2015 20:28 Titel: |
 |
|
Mich würde übrigens interessieren, wie ein konkretes wohldefiniertes nicht-stetiges lineares Funktional auf einem separablen Hilbertraum aussieht. Anders formuliert: Gesucht ist eine Folge  \in \mathbb{C}^{\mathbb N}) komplexer Zahlen, sodass zwar komplexer Zahlen, sodass zwar  (und damit auch (und damit auch  ), aber für jede Folge ), aber für jede Folge  \in \mathbb C^{\mathbb N}) mit mit  trotzdem trotzdem 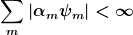 gilt. gilt.
Ich kann keine finden.
Ein Vorschlag war die Delta-Distribution. Wir haben ja nun gesehen, dass diese kein wohldefiniertes lineares Funktional auf L² ist. Ich zeige mal kurz, inwiefern sie das Problem in dieser Formulierung nicht löst: Die Delta-Distribution entspricht ja bekanntlich den Fourierkoeffizienten  (eigentlich auch mit negativen Indizes, aber das ändert am Kern des Problems gar nichts). Nun wählt man zum Beispiel (eigentlich auch mit negativen Indizes, aber das ändert am Kern des Problems gar nichts). Nun wählt man zum Beispiel  und hat das Problem, dass und hat das Problem, dass  . . |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 04. Apr 2015 21:25 Titel: TomS Verfasst am: 04. Apr 2015 21:25 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: | | Aber einen größeren Hilbertraum als S' kenne ich jedenfalls nicht. |
OK, mal suchen ...
Andere Frage: nachdem separable Hilberträume isometrisch isomorph sind, ist ein "größerer" Hilbertraum sowieso mehr als fraglich.
| Jayk hat Folgendes geschrieben: | | Ich habe mir die Argumentation im Cohen-Tannoudji durchgelesen. Besonders lehrreich war sie nicht. |
Dachte ich mir.
| Jayk hat Folgendes geschrieben: | | Ich weiß nicht, wozu die Diskussion im Buch gut sein soll. |
Ja, für mich ist das alles inzwischen ziemlich seltsam. Laut der Axiome der QM wird ein separabler Hilbertraum vorausgesetzt. Demnach sind Distributionen etc. sowieso "pathologisch"; man müsste eigtl. immer entsprechende Wellenpakete betrachten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 05. Apr 2015 11:06 Titel: TomS Verfasst am: 05. Apr 2015 11:06 Titel: |
 |
|
Nur als Idee:
Bei

funktioniert das für

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Apr 2015 11:22 Titel: index_razor Verfasst am: 05. Apr 2015 11:22 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Irgendwie verstehe ich meine eigene Idee nicht mehr :-(
Ich fasse mal ein paar Gedanken zusammen, und hoffe, ihr könnt mir ein paar weitere Hinweise geben.
Gemäß der Axiome der QM formulieren wir diese in einem separablen Hilbertraum; ein Beispiel ist der L2 über R. Allerdings ist dieser für viele praktische Anwendungen "zu klein"; so kann man im L2[R] die Observablen x und p nicht diskutieren, da diese in diesem Raum nicht selbstajungiert sind; als solche müssten sie einen vollständigen Satz von Eigenfunktionen in L2[R] haben; die "verallgemeinerten Eigenfunktionen" sind jedoch nicht Elemente von L2[R], da nicht quadratintegrabel. Daraus folgt, dass man den Abschluss von L2[R] betrachten muss, um x und p vernünftig diskutieren zu können.
|
Ich bin nicht ganz einverstanden mit dieser Formulierung. Selbstadjungierte Operatoren müssen nicht unbedingt einen vollständigen Satz von Eigenfunktionen in L² haben. Das gilt im allgemeinen nur für kompakte Operatoren. Der Operator  \mapsto x f(x)) ist selbstadjungiert, denn er ist symmetrisch und läßt sich sinnvoll auf einer dichten Teilmenge von L² definieren (z.B. den glatten Funktionen mit kompaktem Träger = ist selbstadjungiert, denn er ist symmetrisch und läßt sich sinnvoll auf einer dichten Teilmenge von L² definieren (z.B. den glatten Funktionen mit kompaktem Träger =  ), besitzt aber überhaupt keinen Eigenwert und folglich auch keine Eigenfunktion in L². Das heißt aber nicht, daß man ihn auf L² nicht sinnvoll diskutieren kann. Man kann z.B. auch ohne Eigenfunktionen die Diagonalisierung von X diskutieren, indem man den Spektralsatz verwendet. Lediglich wenn man explizite Lösungen der Gleichung ), besitzt aber überhaupt keinen Eigenwert und folglich auch keine Eigenfunktion in L². Das heißt aber nicht, daß man ihn auf L² nicht sinnvoll diskutieren kann. Man kann z.B. auch ohne Eigenfunktionen die Diagonalisierung von X diskutieren, indem man den Spektralsatz verwendet. Lediglich wenn man explizite Lösungen der Gleichung  sucht, kommt man mit L² nicht mehr aus. sucht, kommt man mit L² nicht mehr aus.
| Zitat: |
Bis hierher reden wir nicht vom Dualraum sondern vom Abschluss eines Raumes. Ich dachte nun, dass der Abschluss ebenfalls als Hilbertraum (im Sinne der Konstruktion der rigged Hilbert spaces bzw. Gelfand triples) aufgefasst werden kann. Damit sind wir aber unmittelbar beim Dualraum als Raum linearer Funktionale.
|
Ich denke nicht, daß der rigged Hilbertraum ein Hilbertraum im eigentlichen Sinne ist. Er definiert doch kein inneres Produkt, sondern nur die Paarung ) mit Testfunktionen f. mit Testfunktionen f.
| Zitat: |
Mir ist nicht ganz klar, welche Bedingungen diese Funktionale genau erfüllen müssen. Insbs. denke ich aber, das man mit der o.g. Konstruktion auch zulassen muss, dass diese Funktionale nicht mehr nach C sondern in den Abschluss von C einschließlich Unendlich abbilden (genauso wie im Abschluss von L2 nicht-normierbare Funktionen enthalten sind).
|
So wie ich es verstanden habe, sind diese Funktionale stetig und linear auf einer dichten Teilmenge von L². Stetig sind sie bezüglich der Topologie dieser Teilmenge, die typischerweise feiner ist als die von L² selbst, d.h. Konvergenz in der Teilmenge impliziert Konvergenz im L², aber nicht umgekehrt. (Z.b. impliziert die Konvergenz in  bzgl. der Supremumsnorm, die L²-Konvergenz.) Man fordert wie gesagt nicht, daß sich diese Funktionale sinnvoll auf ganz L² fortsetzen lassen müssen und deswegen muß man auch nicht fordern, daß sie auf einen (wie auch immer definierten) "Abschluß" von C abbilden. C selbst reicht. bzgl. der Supremumsnorm, die L²-Konvergenz.) Man fordert wie gesagt nicht, daß sich diese Funktionale sinnvoll auf ganz L² fortsetzen lassen müssen und deswegen muß man auch nicht fordern, daß sie auf einen (wie auch immer definierten) "Abschluß" von C abbilden. C selbst reicht.
| Zitat: |
Demnach würde ich zunächst behaupten, dass der Dualraum L2*[R] zu L2[R] exakt wieder der L2*[R] ist, d.h. es liegt Selbst-Dualität vor. Lasse ich nun einige Einschränkungen für die linearen Funktionale fallen, so sind die Distributionen im Sinne eines Schwarz-Raumes zulässig. Und damit dachte ich, dass dies auch für den Abschluss gelten müsse, d.h. dass der Dualraum des Abschlusses wieder auf den Abschluss führt.
Gilt das? Ich kenne den Beweis für L2, nicht jedoch für den Abschluss.
|
Wenn ich richtig interpretiere, was du oben als "Abschluß" von L² bezeichnest, dann ist das dasselbe wie die "Distributionen im Sinne eines Schwartz-Raumes", von denen du hier sprichst. Man betrachtet ja nicht den Dualraum des "Abschlusses", sondern den Dualraum irgendwelcher Testfunktionen, die dicht in L² liegen. Dieser Raum "schließt L² ab" in dem Sinne, daß ich auch verallgemeinerte Lösungen der Eigenwertgleichungen  von Operatoren mit kontinuierlichem Spektrum betrachten kann. von Operatoren mit kontinuierlichem Spektrum betrachten kann.
| Zitat: |
Nun ein weiterer Punkt, den ich nicht mehr verstehe: wenn man sich auf den L2[R] beschränkt, ist zunächst L2*[R] = L2[R] und die eingangs zitierte Feststellung bzgl. der Bras und Kets ist falsch;
|
Ja, so ist es. Allerdings gibt es dann weder einen Bra noch einen Ket mit genau definiertem Ort bzw. Impuls. Wem das nicht gefällt, der darf sich eben nicht von vornherein auf den L² beschränken, sondern muß ihn mit Eigendistributionen "auftakeln".
| Zitat: |
wenn meine hier diskutierte Idee richtig ist, dann gilt dies auch für den Abschluss, und sowohl die eingangs zitierte Feststellung sowie mein Beispiel sind falsch (wiederum wäre der Dualraum mit Raum identisch). |
Ich denke die eingangs zitierte Feststellung legt sich nicht auf den L² fest. Die Testfunktionen sind aber nicht vollständig bzgl. der Norm im L². Deswegen gilt auch nicht die Isomorphie zwischen Bras und Kets, sondern es gibt "mehr" Bras als Kets. Ich denke die ursprüngliche Aussage im Cohen-Tannoudji drückt einfach den schon festgesetellten Sachverhalt
' \subset \mathcal{D}') aus. (Bzw. die analoge Aussage mit irgendeinem anderen Testfunktionenraum.) aus. (Bzw. die analoge Aussage mit irgendeinem anderen Testfunktionenraum.) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 06. Apr 2015 12:04 Titel: TomS Verfasst am: 06. Apr 2015 12:04 Titel: |
 |
|
Weitgehende Zustimmung.
x ist selbstadjungiert, p etc. sind meiner Erinnerung nach zunächst lediglich wesentlich-selbstadjungiert, da nicht auf L2 sondern nur auf Cn definierbar.
Dennoch findet man auch die Aussage, dass auch x nur wesentlich-selbstadjungiert (und damit abschließbar) ist, was wieder auf den Abschluss von L2 führt.
Die Aussage von C.-T. ist dann sinnvoll, wenn man explizit zwischen H und H* unterscheiden möchte. In der QM kann und darf man das m.E. jedoch nicht tun, wenn man die Bornsche Regel verwenden möchte: die Wahrscheinlichkeit, nach Präparation eines Zustandes |u> den Zustand |v> zu messen, folgt aus <v|u>. Es ist sicher mathematisch möglich, dass <v| in einem größeren Raum als |u> lebt, aber physikalisch sinnvoll ist das wohl kaum; was wären das für physikalische Zustände <v|, die ich zwar nicht als Ket präparieren, auf die ich jedoch im Sinne einer Messung bzw. der Bornschen Regel projizieren kann?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 06. Apr 2015 16:44 Titel: Jayk Verfasst am: 06. Apr 2015 16:44 Titel: |
 |
|
Ein Operator  auf auf  mit mit  ist doch genau dann abschließbar, wenn es einen Operator ist doch genau dann abschließbar, wenn es einen Operator  gibt, sodass, wann immer gibt, sodass, wann immer  gilt, auch gilt, auch  folgt. folgt.
Ein Operator ist wesentlich selbstadjungiert, wenn er abschließbar ist und sein Abschluss selbstadjungiert ist.
 . .
Weder der Ortsoperator, noch der Impulsoperator p sind doch auf ganz L² definierbar, oder? Problemlos sind die Definitionen auf dem Schwartzraum  . Der Abschluss von x ist definiert auf den L²-Funktionen, die auch . Der Abschluss von x ist definiert auf den L²-Funktionen, die auch  \vert^2 < \infty) erfüllen (das sind nicht alle). Auf diesem Raum ist er selbstadjungiert, also ist x wesentlich selbstadjungiert. erfüllen (das sind nicht alle). Auf diesem Raum ist er selbstadjungiert, also ist x wesentlich selbstadjungiert.
PS: TomS, danke für die Idee! Ich denke, das funktioniert. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Apr 2015 10:57 Titel: index_razor Verfasst am: 07. Apr 2015 10:57 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Weitgehende Zustimmung.
x ist selbstadjungiert, p etc. sind meiner Erinnerung nach zunächst lediglich wesentlich-selbstadjungiert, da nicht auf L2 sondern nur auf Cn definierbar.
|
Ich denke man definiert p auf einer Teilmenge der absolutstetigen L² Funktionen. Die sind fast überall differenzierbar und mehr braucht man ja für L² nicht. Dann nimmt man  . .
| Zitat: |
Dennoch findet man auch die Aussage, dass auch x nur wesentlich-selbstadjungiert (und damit abschließbar) ist, was wieder auf den Abschluss von L2 führt.
|
Ok, ich hatte noch im Hinterkopf, daß es da bzgl. des Definitionsbereichs Unterschiede gibt. Ich verstehe allerdings noch nicht so richtig, was du mit "Abschluß von L²" meinst. Meinst du das Gelfand-Tripel? (Dann verstehe ich, glaube ich, den Zusammenhang zum Abschluß des Operators x nicht.)
| Zitat: |
Die Aussage von C.-T. ist dann sinnvoll, wenn man explizit zwischen H und H* unterscheiden möchte. In der QM kann und darf man das m.E. jedoch nicht tun, wenn man die Bornsche Regel verwenden möchte: die Wahrscheinlichkeit, nach Präparation eines Zustandes |u> den Zustand |v> zu messen, folgt aus <v|u>. Es ist sicher mathematisch möglich, dass <v| in einem größeren Raum als |u> lebt, aber physikalisch sinnvoll ist das wohl kaum; was wären das für physikalische Zustände <v|, die ich zwar nicht als Ket präparieren, auf die ich jedoch im Sinne einer Messung bzw. der Bornschen Regel projizieren kann? |
Ich denke man betrachtet sie als idealisierte Eigenzustände zu kontinuierlichen Meßwerten, die nur näherungsweise präpariert werden können. "Näherungsweise" würde ich dann im Sinne des schwachen Grenzwertes von regulären (also durch Funktionen darstellbaren) Distributionen interpretieren. Sie völlig auszuschließen erscheint mir irgendwie seltsam, denn man rechnet ja dauernd mit "Impulseigenzuständen"  , die ja eben nicht aus L² stammen. Ich denke auch nicht, daß der Formalismus in dem Sinne asymmetrisch bzgl. Präparation und Messung ist. Wenn du verallgemeinerte Zustände als "out"-Zustände zuläßt, die mit z.B. glatten "in"-Zuständen gepaart werden können, kannst du das doch auch umgekehrt machen und die "in"-Zustände als Elemente des Biduals von Testfunktionen betrachten. Das sollte die Symmetrie wieder herstellen. Oder gibt es einen Grund dagegen? , die ja eben nicht aus L² stammen. Ich denke auch nicht, daß der Formalismus in dem Sinne asymmetrisch bzgl. Präparation und Messung ist. Wenn du verallgemeinerte Zustände als "out"-Zustände zuläßt, die mit z.B. glatten "in"-Zuständen gepaart werden können, kannst du das doch auch umgekehrt machen und die "in"-Zustände als Elemente des Biduals von Testfunktionen betrachten. Das sollte die Symmetrie wieder herstellen. Oder gibt es einen Grund dagegen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
 TomS Verfasst am: 07. Apr 2015 22:28 Titel: TomS Verfasst am: 07. Apr 2015 22:28 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Ich denke man betrachtet sie als idealisierte Eigenzustände zu kontinuierlichen Meßwerten, die nur näherungsweise präpariert werden können. "Näherungsweise" würde ich dann im Sinne des schwachen Grenzwertes von regulären (also durch Funktionen darstellbaren) Distributionen interpretieren. Sie völlig auszuschließen erscheint mir irgendwie seltsam, denn man rechnet ja dauernd mit "Impulseigenzuständen"  , die ja eben nicht aus L² stammen. Ich denke auch nicht, daß der Formalismus in dem Sinne asymmetrisch bzgl. Präparation und Messung ist. Wenn du verallgemeinerte Zustände als "out"-Zustände zuläßt, die mit z.B. glatten "in"-Zuständen gepaart werden können, kannst du das doch auch umgekehrt machen und die "in"-Zustände als Elemente des Biduals von Testfunktionen betrachten. Das sollte die Symmetrie wieder herstellen. Oder gibt es einen Grund dagegen? , die ja eben nicht aus L² stammen. Ich denke auch nicht, daß der Formalismus in dem Sinne asymmetrisch bzgl. Präparation und Messung ist. Wenn du verallgemeinerte Zustände als "out"-Zustände zuläßt, die mit z.B. glatten "in"-Zuständen gepaart werden können, kannst du das doch auch umgekehrt machen und die "in"-Zustände als Elemente des Biduals von Testfunktionen betrachten. Das sollte die Symmetrie wieder herstellen. Oder gibt es einen Grund dagegen? |
Ja, sehe ich genauso. Natürlich muss die Symmetrie erhalten bleiben, also für Bra und Ket
1) L2- = quadratintegrable Funktionen bzw. eine genügend glatte Untermenge oder
2) Abschluss des L2 (bzw. der Operatoren x, p) mittels delta-Distribution, ebener Welle usw.
(2) sehe ich dabei als "Idealisierung", "Bequemlichkeit" beim Rechnen o.ä.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|








 Zum Beispiel ist
Zum Beispiel ist 