| Autor |
Nachricht |
Masseltof
Anmeldungsdatum: 01.01.2011
Beiträge: 43
|
 Masseltof Verfasst am: 07. Aug 2012 11:28 Titel: Was macht die Bewegungsrichtung aus? |
 |
|
Guten Tag.
Ich wiederhole gerade etwas Physik und wollte sicher gehen, dass meine Annahme richtig ist.
Die Bewegung eines Teilchens wird bestimmt durch Richtung, Betrag, Orientierung des Geschwindigkeitsvektors.
Dessen Richtung, Betrag, Orientierung werden beeinflusst durch die auf das Teilchen wirkenden Kräfte/Beschleunigungen.
Grüße |
|
 |
planck1858
Anmeldungsdatum: 06.09.2008
Beiträge: 4542
Wohnort: Nrw
|
| planck1858 Verfasst am: 07. Aug 2012 11:34 Titel: |
|
|
Das sieht schonmal gut aus.
_________________
Die Naturwissenschaft braucht der Mensch zum Erkennen, den Glauben zum Handeln. (Max Planck)
"I had a slogan. The vacum is empty. It weighs nothing because there's nothing there. (Richard Feynman) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 07. Aug 2012 11:52 Titel: |
|
|
Ganz allgemein folgt die Bewegungsgleichung aus einer Lagrangefunktion. Im einfachsten Fall erhält man
)
Integration der Bewegungsleichung plus Festlegung der Anfangsbedingung für Ort und Geschwindigkeit legt also den Ortsvektor als Funktion der Zeit fest.
Bei einer reinen Betrachtung des Geschwindigkeitsvektors plus der Anfangsbedingung = der Anfangsgeschwindigkeit fehlt noch die Anfangsbedingung für den Ort.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 07. Aug 2012 14:58 Titel: |
|
|
|
Was ist übrigens unter "Orientierung" zu verstehen - im Unterschied zur Richtung? |
|
|
Richtungsweiser
Gast
|
| Richtungsweiser Verfasst am: 07. Aug 2012 19:04 Titel: |
|
|
für franz
Seien zwei (nicht zusammenfallende) Punkte A und B.
Der Vektor von A nach B hat dieselbe Richtung wie der Vektor von B nach A.
Die Vektoren von A nach B und von B nach A haben entgegengesetzte Orientierung! |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 07. Aug 2012 19:17 Titel: |
|
|
| Richtungsweiser hat Folgendes geschrieben: | Seien zwei (nicht zusammenfallende) Punkte A und B.
Der Vektor von A nach B hat dieselbe Richtung wie der Vektor von B nach A. |
Nein, hat er sicher nicht, weil der Vektor eben eine gerichtete Größe ist. Der Vektor von A nach B und der Vektor von B nach A sind zwei verschiedene Vektoren; sie unterscheiden sich um eine Vorzeichen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Rmn
Anmeldungsdatum: 26.01.2010
Beiträge: 473
|
| Rmn Verfasst am: 07. Aug 2012 19:30 Titel: |
|
|
|
So, wie Richtungsweiser sagt, werden Vektoren in reiner Geometrie(in der Schule) manchmal betrachtet, d.h. wörtlich als "Pfeile" mit Länge, Richtung und Orientierung. :/ |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 07. Aug 2012 19:36 Titel: |
|
|
Aber "von A nach B" hat doch schon Richtung und Orientierung.
Kein Mensch sagt doch "ein Pfeil zwischen A und B - wobei wir jetzt nicht unterscheiden ob von A nach B oder von B nach A - oder eine Linie zwischen A und B - wobei ich euch nicht verrate, an welches Ende ich den Pfeil male" und "der Startpunkt ist bei A". Das ist doch b...s...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Rmn
Anmeldungsdatum: 26.01.2010
Beiträge: 473
|
| Rmn Verfasst am: 07. Aug 2012 20:00 Titel: |
|
|
Ich denke man versucht hier die Richtung so zu definieren, dass wenn ein Vektor 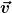 gegeben ist, dann haben alle Vektoren des Vektorraums  mit  dieselbe Richtung, vielleicht abgesehen von dem Nullvektor. Davon alle mit t>0 eine und t<0 andere Orientierung.
Wozu das gut sein sollte, ist mit ehrlich gesagt auch schleierhaft. Es macht erst Sinn über Orientierung zu reden, wenn man Normalenvektoren betrachtet. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 07. Aug 2012 20:30 Titel: |
|
|
OT
Meine Herren!
Kann es vielleicht sein, daß wir hier bezüglich der generellen Talfahrt (Infantilisierung) des mathematisch - naturwissenschaftlichen Schulunterrichts in Deutschland nicht ganz auf dem laufenden sind - fragt sich ein alter Ossi.  |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 07. Aug 2012 21:45 Titel: |
|
|
Die Idee von RNM ist OK, die von franz aber - leider - auch möglich ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 08. Aug 2012 09:09 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Die Idee von RNM |
Hüstel ...  ...  |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 08. Aug 2012 09:12 Titel: |
|
|
oh, sorry, aber ich dachte, Rmn ist symmetrisch in mn
:D
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Masseltof
Anmeldungsdatum: 01.01.2011
Beiträge: 43
|
| Masseltof Verfasst am: 08. Aug 2012 10:53 Titel: |
|
|
Guten Tag.
Es wäre vielleicht sinnvoll zu erwähnen, dass ich nicht mehr in die Schule gehe und Chemie an einer Universität in Deutschland studiere.
In der Universitätsmathematik (Mathe für NaWis) bekommt es ebenfalls so beigebracht und wenn ich mich recht erinnere schreibt der Papula es ebenso.
Wie die Physiker hätte ich als Chemiker gerne auch eine Mathevorlesung die etwas genauer aufgebaut ist, aber das würde zeitlich wohl weniger gehen.
Ich würde gerne fragen, wie hier im Forum Vektoren denn allgemein zu definieren sind. (R^2, R^3)
Für eine grobe Beschreibung ist die Verwendung von Richtung (wo liegt der Vektor),Orientierung(welches Vorzeichen trägt er), Betrag(selbstklärend), eigentlich ganz sinnvoll?
Natürlich könnte man auch Richtung und Orientierung zusammenfassung, aber warum nicht auf alte KOnventionen zurückgreifen?
Gruß |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 09. Aug 2012 05:00 Titel: |
|
|
| Masseltof hat Folgendes geschrieben: | | Ich würde gerne fragen, wie hier im Forum Vektoren denn allgemein zu definieren sind. (R^2, R^3) |
Vektoren / Vektorräume sind feststehende mathematische Begriffe. Beispiele n-Tupel, Ortsvektoren, Translationen, reelle Funktionene u.a. Man nutzt sie von Fall zu Fall in der Physik für gerichtete Größen (Kraft, Geschwindigkeit, Feldstärke) und braucht dafür zumindest Betrag und Richtung. ("Alte Konventionen" sind mir nicht bekannt.) |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 09. Aug 2012 05:06 Titel: |
|
|
OT | TomS hat Folgendes geschrieben: | | aber ich dachte, Rmn ist symmetrisch in mn |
Also ab heute: Ridschi. |
|
|
Masseltof
Anmeldungsdatum: 01.01.2011
Beiträge: 43
|
| Masseltof Verfasst am: 09. Aug 2012 09:52 Titel: |
|
|
| franz hat Folgendes geschrieben: | | Masseltof hat Folgendes geschrieben: | | Ich würde gerne fragen, wie hier im Forum Vektoren denn allgemein zu definieren sind. (R^2, R^3) |
Vektoren / Vektorräume sind feststehende mathematische Begriffe. Beispiele n-Tupel, Ortsvektoren, Translationen, reelle Funktionene u.a. Man nutzt sie von Fall zu Fall in der Physik für gerichtete Größen (Kraft, Geschwindigkeit, Feldstärke) und braucht dafür zumindest Betrag und Richtung. ("Alte Konventionen" sind mir nicht bekannt.) |
Warum sollte man denn dann nicht von einer Orientierung sprechen?
Zeigen zwei Vektoren in eine Richtung und haben den selben Betrag so können sie dennoch eine unterschiedliche Orientierung haben.
OT:
Warum kritisiert eigentlich jeder Mensch (selbst das Lehrpersonal) den Unterricht, aber ändert daran nichts?
Die Bildungsminister treffen sich ein paar Mal im Jahr und es kommt im Prinzip nichts bei rum.
Das Bildungssystem an der Universität verfällt prinzipiell auch. Wobei eines das andere bedingt. |
|
|
Benutzerename
Gast
|
| Benutzerename Verfasst am: 09. Aug 2012 12:15 Titel: |
|
|
[quote="Masseltof]Warum sollte man denn dann nicht von einer Orientierung sprechen? Zeigen zwei Vektoren in eine Richtung und haben den selben Betrag so können sie dennoch eine unterschiedliche Orientierung haben. [/quote]Nein, Richtung ist zum Beispiel durch die Punkte A nach B  gegeben (ohne Normierung).
Natürlich ist das Wort dafür egal, aber halt nur eins, es gibt später noch genug Komplikationen bei Vektoren,Tensoren usw. |
|
|
Rmn
Anmeldungsdatum: 26.01.2010
Beiträge: 473
|
| Rmn Verfasst am: 09. Aug 2012 12:55 Titel: |
|
|
| Masseltof hat Folgendes geschrieben: | | franz hat Folgendes geschrieben: | | Masseltof hat Folgendes geschrieben: | | Ich würde gerne fragen, wie hier im Forum Vektoren denn allgemein zu definieren sind. (R^2, R^3) |
Vektoren / Vektorräume sind feststehende mathematische Begriffe. Beispiele n-Tupel, Ortsvektoren, Translationen, reelle Funktionene u.a. Man nutzt sie von Fall zu Fall in der Physik für gerichtete Größen (Kraft, Geschwindigkeit, Feldstärke) und braucht dafür zumindest Betrag und Richtung. ("Alte Konventionen" sind mir nicht bekannt.) |
Warum sollte man denn dann nicht von einer Orientierung sprechen?
Zeigen zwei Vektoren in eine Richtung und haben den selben Betrag so können sie dennoch eine unterschiedliche Orientierung haben.
|
Wenn ich einer zufällig gewählten Person erzähle, dass ein Pfeil, der nach Norden zeigt, selbe Richtung hat, wie ein Pfeil, der nach Süden zeigt, werde ich höhstwahrscheinlich für verrückt erklärt. Das ist schon Grund genug, um solche Namensgebungen zu vermeiden. Da hätte man sich wirklich lieber andere Wörter genommen, als wohlbekannte, gebräuchliche Wörter neu zu definieren.
Für Physiker und Standardmathematiker sind Vektoren algebraisch definiert; sie sind Elemente eines Vektorraums. Eine rein geometrische Betrachtung als Pfeilklasse ist für uns mehr oder weniger nutzlos. Allein schon deswegen, weil Algebra "mächtiger" als Geometrie ist, d.h. man kann mit Algebra komplette Geometrie und viel mehr beschreiben.
Es gibt Vektoren, die überhaupt nichts mit unserem gewöhnlichen Raum zutun haben und damit als Pfeile überhaupt nicht sinnvoll vorstellbar. Sie spielen aber trotzdem eine essentielle Rolle und Mathematik und Physik. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 10. Aug 2012 23:09 Titel: |
|
|
| Masseltof hat Folgendes geschrieben: | | Zeigen zwei Vektoren in eine Richtung und haben den selben Betrag so können sie dennoch eine unterschiedliche Orientierung haben. |
Nein, können sie nicht. Und ich habe auch schon mal geschrieben, warum das so ist:
| TomS hat Folgendes geschrieben: | | ... [ein Vektor] "von A nach B" hat ... schon [Länge], Richtung und Orientierung. |
Die Orientierung ist bereits durch die Richtung "von A nach B" festgelegt. Eine weitere Information ist nicht notwendig; und es fehlt auch keine Information.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Masseltof
Anmeldungsdatum: 01.01.2011
Beiträge: 43
|
| Masseltof Verfasst am: 11. Aug 2012 00:37 Titel: |
|
|
Hallo.
Genau die Argumentation haben wir in der Schule geführt und dennoch beharrte unser Lehrer auf Orientierung.
Danke für tollen Erklärungen.
Grüße |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 11. Aug 2012 06:49 Titel: |
|
|
OT
Wichtig erstmal die Klärung für Dich!
Ob dann noch weitere Diskussionen im Unterricht sinnvoll sind, das kannst nur Du alleine wissen. [Ich hatte früher öfter Krawall und lebe trotzdem noch.] Auf alle Fälle würde ich jetzt sorgfältig lernen und alle Aufgaben möglichst gut verstehen und lösen. Ansonsten sind ja auch noch da.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
| DrStupid Verfasst am: 11. Aug 2012 12:02 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Die Orientierung ist bereits durch die Richtung "von A nach B" festgelegt. Eine weitere Information ist nicht notwendig; und es fehlt auch keine Information. |
Das ist eine Definitionsfrage. Die Trennung von Richtung und Orientierung kenne ich auch aus meiner Schulzeit (nur dass die Orientierung damals Richtungssinn genannt wurde). Dahinter stand die Festlegung, dass zwei Vektoren die gleiche Richtung haben, wenn ihr Skalarprodukt Null ist. Wozu das gut sein soll, habe ich allerdings nie verstanden. Mit ist noch kein Fall begegnet, in dem die Richtung eines Vektors mit Hilfe von Skalarprodukten definiert wurde und ich kann mir auch nicht vorstellen, wozu das gut sein soll. Um einen n-dimensionalen Vektor eindeutig zu charakterisieren brauche ich n Werte. Für den Betrag brauche ich einen und für die Richtung normalerweise n-1. Welche Sinn könnte es haben, die Richtung so zu definieren, dass diese n-1 Werte unter bestimmten Bedingungen nicht ausreichen und ein zusätzlicher Parameter benötigt wird, der einen von zwei Werten annehmen kann? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
| TomS Verfasst am: 11. Aug 2012 12:27 Titel: |
|
|
Wir fassen zusammen: es gibt diese Trennung von 'Richtung' und 'Orientierung', wir verstehen jedoch nicht, wozu das gut sein soll bzw. ob die Begriffe überhaupt korrekt verwendet werden.
Der Begriff, der eigtl. definiert werden soll, ist sicher nicht die Richtung sondern die sogenannte Kollinearität: zwei Vektoren a und b sind kollinear, wenn eine Zahl lambda existiert, so dass
gilt.
http://de.wikipedia.org/wiki/Kollinearit%C3%A4t
| DrStupid hat Folgendes geschrieben: | | ... dass zwei Vektoren die gleiche Richtung haben, wenn ihr Skalarprodukt Null ist. |
Du meinst sicher nicht, dass ihr Skalarprodukt Null ist, sondern z.B. das Kreuzprodukt; oder dass ihr Skalarprodukt das Produkt ihrer Beträge ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
| DrStupid Verfasst am: 11. Aug 2012 13:36 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | DrStupid hat Folgendes geschrieben: | | ... dass zwei Vektoren die gleiche Richtung haben, wenn ihr Skalarprodukt Null ist. |
Du meinst sicher nicht, dass ihr Skalarprodukt Null ist, sondern z.B. das Kreuzprodukt; oder dass ihr Skalarprodukt das Produkt ihrer Beträge ist. |
Danke für die Korrektur. Genau so war es gemeint. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 11. Aug 2012 13:50 Titel: |
|
|
|
In dem alten DDR Buch wird der Vektorbegriff induktiv entwickelt (ausgehend von Verschiebungen der Ebene / Geometrie) als Pfeilklasse [A,A'] zu einer Verschiebung, dann räumlich und anschließend die Rechengesetze usw. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5043
|
| DrStupid Verfasst am: 11. Aug 2012 14:14 Titel: |
|
|
| franz hat Folgendes geschrieben: | | In dem alten DDR Buch wird der Vektorbegriff induktiv entwickelt (ausgehend von Verschiebungen der Ebene / Geometrie) als Pfeilklasse [A,A'] zu einer Verschiebung, dann räumlich und anschließend die Rechengesetze usw. |
Das Schulbuch habe ich zwar nicht mehr zur Hand aber ich habe hier noch ein zerfleddertes Exemplar der kleinen Enzyklopädie Mathematik herumliegen und da geht es zum Thema Vektoren gleich im ersten Absatz mit der Definition des Vektorraumes aus der linearen Algebra los:
"Ein Vektorraum ist eine Menge von Elementen, die man zueinander addieren und die man mit Zahlen multiplizieren kann, wobei die üblichen Rechenregeln gelten."
Im Kapitel Vektoralgebra (in dem speziell Vektoren im dreidimensionalen Raum behandelt werden) heißt es dann:
"Zwei Vektoren im Raum sind genau dann gleich, wenn je zwei ihrer Repräsentanten in Betrag und Richtung übereinstimmen."
Ähnlich sieht es beim Bronstein-Semendjajew aus. Hier die beiden ersten Sätze im Kapitel Vektorrechnung:
"Größen, deren Werte durch reelle Zahlen ausgedrückt werden können, heißen Skalare (z.B. Masse, Ladung, Temperatur, Arbeit usw.). Die Größen, dagegen, die durch eine Zahlenangabe und zusätzlich eine Richtung im Raum charakterisiert sind, nennt man Vektoren (z.B. Geschwindigkeit, Beschleunigung, Kraft, elektrische und magnetische Feldstärke usw.)."
Wahrscheinlich kommt die Geschichte mit der Orientierung nicht aus der Mathematik, sondern aus der Didaktik. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 11. Aug 2012 20:17 Titel: |
|
|
Das denke ich auch.
Und wenn wir schon ostzonal schwelgen: Lexikon der Mathematik (wurde übrigens in der Wendezeit aus einigen Bibliotheken geschmissen): Vektoren = Elemente von Vektorräumen, linear mit den Axiomen ... (4 Seiten). |
|
|
gast0012
Gast
|
| gast0012 Verfasst am: 11. Aug 2012 22:54 Titel: |
|
|
Ein einfacher Unterschied mathematisch aufgezeigt, wäre eine Richtungsangabe mit der Steigung k oder eine Richtungsangabe mit winkel phi
in radiant.
Während phi in Radiant sowohl Richtung als auch Orientierung bestimmt.
Bestimmt k als Steigung nur die Richtung nicht aber die Orientierung.
Wenn man jetzt als Richtungsangabe bereits die Pfeilspitze mit inkludiert ist das Definitionssache,
Mathematisch lässt sich das eindeutig mit k und phi unterscheiden.
k gibt die Richtung an aber niemals die Orientierung |
|
|
|
Registrieren
Login
FAQ
Suchen
