| Autor |
Nachricht |
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
 Erster Admiral Verfasst am: 14. Feb 2022 19:30 Titel: Rotationsymmetrie in Schwarzschild-Metrik? |
 |
|
Wie kann ich mathematisch präzise zeigen, dass die Schwarzschildmetrik eine Rotationssymmetrie hat?
An sich ist das ziemlich klar, weil der winkelabhängige Teil der Metrik die S^2-Metrik ist.
Wenn ich das jetzt aber mathematisch präzise beweisen soll, bin ich etwas ratlos. Was wäre denn eine sinnvolle Definition von Rotationssymmetrie mit der ich da arbeiten kann?
Eine Idee von mir wäre es zu zeigen, dass die Killing-Gleichung für die Rotations-Generatoren erfüllt ist, aber das scheint mir als würde man mit Kanonen auf Spatzen schießen.
Eine sinnvolle Definition wäre doch:
g ist genau dann Rotationsinvariant
wenn:
mit Schwarzschild-Koordinaten
)
und
mit Schwarzschild-Koordinaten
)
dann
für alle
 ) .
Oder?
M bezeichnet die Mannigfaltigkeit und g den Metrischen Tensor.
Zwei Beiträge zusammengefasst. Steffen |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 15. Feb 2022 18:55 Titel: Re: Rotationsymmetrie in Schwarzschild-Metrik? |
|
|
| Erster Admiral hat Folgendes geschrieben: | Wenn ich das jetzt aber mathematisch präzise beweisen soll, bin ich etwas ratlos. Was wäre denn eine sinnvolle Definition von Rotationssymmetrie mit der ich da arbeiten kann?
|
Die Definition der Rotationssysmmetrie wäre das Verschwinden der Lie-Ableitung
})
entlang der Generatoren 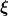 der Rotationsgruppe. Die Killing-Gleichung für 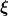ist eine unmittelbare Folge aus (1).
Ich habe es nicht durchgerechnet, aber vielleicht ist es leichter, diese Beziehung direkt zu verwenden. Zumindest spart man sich gegenüber der Killing-Gleichung die Auswertung der Zusammenhangskoeffizienten. Und wenn man 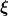in sphärischen Koordinaten ausgedrückt hat, dann läuft es im wesentlichen auf die Berechnung einiger partieller Ableitungen hinaus.
Einer der Generatoren ist ja z.B. einfach  . Für diesen ist Invarianz sogar trivial zu zeigen. Die Bedingung (1) bedeutet nichts anderes, als das die Metrikkoeffizienten nicht von  abhängen.
Aber normalerweise "weiß" man ja von vornherein, daß die Schwarzschildmetrik rotationsinvariant ist, weil man sie unter dieser Bedingung hergeleitet hat. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 15. Feb 2022 19:54 Titel: |
|
|
Allright. Ich kann dann ja die Lie-Ableitung einfach auf die Lie-Ableitung der Komponentenfunktionen reduzieren oder?
also
das würde dann für den ersten Generator ergeben:
Aber dann wäre
 .
Wo liegt der Fehler? |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 15. Feb 2022 20:24 Titel: |
|
|
| Erster Admiral hat Folgendes geschrieben: | Allright. Ich kann dann ja die Lie-Ableitung einfach auf die Lie-Ableitung der Komponentenfunktionen reduzieren oder?
|
Nein, du mußt die Produktregeln anwenden
 = \xi.g_{\mu\nu}\dd x^\mu\otimes\dd x^\nu + g_{\mu\nu}\pounds_\xi(\dd x^\mu\otimes\dd x^\nu).)
Außerdem gilt
 = (\pounds_\xi A)\otimes B + A\otimes(\pounds_\xi B))
und
 |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 15. Feb 2022 21:28 Titel: |
|
|
okay, danke dir!
Ich verstehe noch nicht ganz wie ich die Lie-Ableitung auf ein Tensorfeld anwende, also z.B. was der Ausdruck
bedeutet.
Laut Wikipedia ist das ja definiert durch den Fluss des Vektorfelds  :
 .
Allerdings verstehe ich nicht genau wie ich mit diesem Ausdruck jetzt weiterarbeite. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 15. Feb 2022 21:39 Titel: |
|
|
| Erster Admiral hat Folgendes geschrieben: | okay, danke dir!
Ich verstehe noch nicht ganz wie ich die Lie-Ableitung auf ein Tensorfeld anwende, also z.B. was der Ausdruck
bedeutet.
|
Berechnen kann man das mittels
 = \dd (\xi.f))
Rechts steht also das gewöhnliche Differential einer Funktion.
| Zitat: |
Laut Wikipedia ist das ja definiert durch den Fluss des Vektorfelds :
.
Allerdings verstehe ich nicht genau wie ich mit diesem Ausdruck jetzt weiterarbeite. |
Ja das ist die allgemeine Definition, aber zum Rechnen etwas unhandlich. Man versucht eigentlich immer die Lie-Ableitung auf einfacher zu berechnende Operationen zurückzuführen, wie das Differential oder die Richtungsableitung von Funktionen. Dazu kann man, wie oben, die Beziehung  verwenden. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 16. Feb 2022 13:28 Titel: |
|
|
| Zitat: | Berechnen kann man das mittels
Rechts steht also das gewöhnliche Differential einer Funktion.
|
Okay damit kann ich arbeiten, auch wenn ich den Zusammenhang noch nicht ganz verstehe. Aber Beweise dafür finde ich sicher in etlichen Büchern.
Vielen Dank! |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 16. Feb 2022 13:56 Titel: |
|
|
| Erster Admiral hat Folgendes geschrieben: | | Zitat: | Berechnen kann man das mittels
Rechts steht also das gewöhnliche Differential einer Funktion.
|
Okay damit kann ich arbeiten, auch wenn ich den Zusammenhang noch nicht ganz verstehe. Aber Beweise dafür finde ich sicher in etlichen Büchern.
|
Ja, eine der wichtigsten Beziehungen im Zusammenhang mit der Lie-Ableitung auf Differentialformen ist bestimmt Cartans magische Formel  . Danach würde ich mal suchen. Die solltest du eigentlich in Büchern über Differentialgeometrie schnell finden (gerade nochmal nachgeschlagen in Warner, Foundations of Differentiable Manifolds and Lie Groups, Proposition 2.25). Die ist schon für sich allein recht nützlich, u.a. kann man auch die obige Formel leicht beweisen
und
P.S. Ich habe übrigens die Rechnung mit dem Generator  mal probiert. Man muß zwar relativ viele Terme mitschleppen, aber machbar ist es zumindest. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 17. Feb 2022 11:17 Titel: |
|
|
Vielen Dank!
Ich habe es jetzt auch durchgerechnet und es passt alles!
Dann noch eine weitere Frage:
Was genau ist denn der Zusammenhang zwischen den Generatoren der Rotationsgruppe  (wie sie hier verwendet wurden) die die Lie-Algebra
 erfüllen,
und den Generatoren der SO(3)-Lie-Algebra:
 .
Formal erhalte ich ja  . Aber was genau bedeutet das auf der mathematischen Ebene? Heißt es, dass die Lie-Algebren isomorph sind wenn sie sich nur um einen konstanten Faktor unterscheiden? Heißt es dass die Gruppen identisch sind? |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 17. Feb 2022 12:47 Titel: |
|
|
| Erster Admiral hat Folgendes geschrieben: |
Dann noch eine weitere Frage:
Was genau ist denn der Zusammenhang zwischen den Generatoren der Rotationsgruppe (wie sie hier verwendet wurden) die die Lie-Algebra
erfüllen,
und den Generatoren der SO(3)-Lie-Algebra:
.
Formal erhalte ich ja . Aber was genau bedeutet das auf der mathematischen Ebene?
|
Die  sind die Elemente der Lie-Algebra ) . Dies ist eine reelle Algebra, denn es handelt sich ja im wesentlichen um den Tangentialraum der reellen Mannigfaltigkeit SO(3) an der Einheitstransformation. (Das gilt auch, wenn die Lie-Gruppe eine Gruppe von komplexen Matrizen ist, z.B. ist  = \mathbb{R}) .)
Die  sind Elemente der komplexen Hülle (oder "Komplexifizierung") der Lie-Algebra, d.h. sie stammen aus
_\mathbb{C} = \mathbb{C}\otimes\mathfrak{so}(3)\equiv \mathfrak{so}(3) + i\mathfrak{so}(3).)
Anschaulich gesprochen ist das die Lie-Algebra, die man erhält, wenn man in Linearkombinationen von auch komplexe Zahlen zuläßt.
Für die Darstellungstheorie ist es oft praktischer mit der Komplexifizierung zu arbeiten; siehe z.B. die Definition der Leiteroperatoren für die SU(2) bzw. SO(3). Deswegen verwendet man sie in der Quantenmechanik eigentlich ausschließlich. Dasselbe gilt auch für die Poincarealgebra, an deren Stelle man die komplexifizierte Version _\mathbb{C}=\mathfrak{su}(2)_\mathbb{C}\oplus\mathfrak{su}(2)_\mathbb{C}) verwendet.
| Zitat: |
Heißt es, dass die Lie-Algebren isomorph sind wenn sie sich nur um einen konstanten Faktor unterscheiden? Heißt es dass die Gruppen identisch sind? |
Die Fragen gehen, glaube ich, von etwas falschen Annahmen aus. Die Gruppen sind nicht identisch. Aber man interessiert sich normalerweise eigentlich gar nicht für die Gruppe der komplexifizierten Algebra. Man verwendet sie nur um Darstellungen der ursprünglichen Algebra, und damit der Überlagerungsgruppe der ursprünglichen Gruppe, zu finden, z.B. der SU(2) (für die SO(3)) oder der SL(2,C) (für die SO(1,3)). |
|
|
|
Registrieren
Login
FAQ
Suchen
