| Autor |
Nachricht |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 11. Jan 2020 11:56 Titel: Variationen Palatini-Identität |
 |
|
Zur Herleitung der Einsteingleichungen aus dem Wirkungsprinzip wird häufig die Palatini-Identität verwendet, die lautet:
 - \nabla_{\nu}(\delta \Gamma^{\rho}_{\lambda \mu})
<br />
)
Die kovariante Ableitung von  hat ja nur einen Sinn wenn dieser Ausdruck auch ein Tensor ist. In dem Skript, dass ich dazu gerade lese wird argumentiert, dass das ein Tensor ist, da es eine Differenz von zwei affinen Zusammenhängen darstellt.
Dabei ist mir aufgefallen, dass ich das Prinzip der Variationen nicht ganz verstehe, also warum ist die Differenz zweier affiner Zusammenhänge ?
Bei der üblichen Herleitung der Euler-Lagrange-Gleichungen wird die Variation der Bahn y mit  bezeichnet. Aber das entspricht ja nicht der Differenz zweier Bahnen, oder? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 11. Jan 2020 21:00 Titel: Re: Variationen - gundlegendes Verständnis - Palatini-Identi |
|
|
| Corbi hat Folgendes geschrieben: |
In dem Skript, dass ich dazu gerade lese wird argumentiert, dass das ein Tensor ist, da es eine Differenz von zwei affinen Zusammenhängen darstellt.
Dabei ist mir aufgefallen, dass ich das Prinzip der Variationen nicht ganz verstehe, also warum ist die Differenz zweier affiner Zusammenhänge ?
Bei der üblichen Herleitung der Euler-Lagrange-Gleichungen wird die Variation der Bahn y mit bezeichnet. Aber das entspricht ja nicht der Differenz zweier Bahnen, oder? |
Wieso nicht? Im Prinzip ist es doch genau das. Bei den Bahnen handelt es sich ja oft um Kurven im euklidischen Raum. Für zwei solcher Bahnen , x_B(t)) läßt sich die punktweise Differenz bilden
 = x_B(t) - x_A(t))
Dies ist ein Vektorfeld entlang  und als eigenständiges Objekt kann man es auch als  definieren. Parametrisierst du ) mit irgendeinem  derart, daß alle möglichen Glattheitsbedingungen und  = x_A) erfüllt sind, kannst du diese Differenz bis zur ersten Ordnung
 - x_A = \frac{\partial}{\partial \epsilon}x_B(\cdot, 0)\epsilon + ...)
auswerten. Der lineare Term ist die Variation von . Es handelt sich also anschaulich um die Differenz zweier infinitesimal benachbarter Kurven.
In genau demselben Sinne ist die Aussage über kovariante Ableitungen zu verstehen. Um die Behauptung einzusehen muß man sich nur klar machen, daß eine kovariante Ableitung vollständig durch ihre Wirkung auf Funktionen und Vektorfelder definiert ist. (Für Tensoren anderer Stufen definiert man sie ja mittels Tensorproduktregel und Vertauschbarkeit mit der Kontraktion.)
Für Funktionen gilt  , also
} - \nabla^{(2)})f \equiv 0.\qquad (1))
Für Vektorfelder reicht es zu zeigen, daß } - \nabla^{(2)})X) eine ) -lineare Abbildung ist, also für jede glatte Funktion f gilt
} - \nabla^{(2)})(fX) = f(\nabla^{(1)} - \nabla^{(2)})X.)
(Folgt aus der Produktregel und (1). Additivität ist klar.) Zu solchen Abbildungen gehören Tensorfelder.
Kleine Abschweifung:
Mit demselben Argument sieht man übrigens auch, daß die 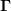 selbst Komponenten von Tensorfeldern sind, sofern man eine Koordinatenableitung bzgl. einer fixen Karte betrachtet. Denn  erfüllt alle Axiome einer kovarianten Ableitung und es gilt
Es wird zwar oft behauptet, daß die 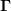auf Grund ihres "Transformationsgesetzes" keine Tensoren sein können, aber wie das Argument oben zeigt, sind solche Aussagen sind mit Vorsicht zu genießen.
Oft sind diese Transformationsgesetze nämlich nicht naturgegeben, und dasselbe dasselbe Objekt unterliegt je nach Gesichtspunkt unterschiedlichen Transformationsgesetzen. Für die Zusammenhangskomponenten 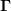ist z.B. wichtig anzugeben, ob ich beim Kartenwechsel auch die Ableitung in der obigen Definition ändere oder nicht. Wenn ja, dann ändere ich auch den durch  definierten Tensor. Ich berechne also nicht die Änderungen der Komponenten eines fixen Tensors unter Kartenwechseln, sondern die Änderung, die resultiert, wenn ich die Karte und den Tensor austausche. Das ergibt natürlich ein anderes Transformationsgesetz.
(Ganz ähnliche Überlegungen gelten auch für den Unterschied zwischen "Skalaren" und "Vektorkomponenten", der nicht von so fundamentaler Bedeutung ist, wie oft suggeriert wird.) |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 13. Jan 2020 14:59 Titel: |
|
|
Vielen Dank für die ausführliche Antwort! Die Abschweifung geht mir für den Moment aber etwas zu weit.
Noch eine Frage zur ART:
Die Schwarzschildlösung ist eine Lösung für  .
Das bedeutet ja, dass auch der Riemann-Tensor null ist und die Schwarzschildlösung eine flache Raumzeit beschreibt. Aber sollte man eine flache Raumzeit nicht immer auf eine Minkowski-Metrik transformieren können ?
Meine Ideen:
-entweder die Schwarschildlösung beschreibt doch keine flache Raumzeit
-oder ich kann es nicht auf eine Minkowski-Metrik transformieren, da der 3-D-Unterraum gekrümmt ist ? |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 13. Jan 2020 17:35 Titel: |
|
|
|
ok im Fließbach steht offenbar Unfug. Da habe ich gefunden, dass die Raumzeit der Schwarzschildlösung flach sei. und Der Riemann-Tensor ist natürlich nicht Null nur weil der Ricci-Tensor 0 ist. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 14. Jan 2020 11:58 Titel: |
|
|
| Corbi hat Folgendes geschrieben: | ok im Fließbach steht offenbar Unfug. Da habe ich gefunden, dass die Raumzeit der Schwarzschildlösung flach sei.
|
Ja, das klingt tatsächlich nach Unfug. Man kann zwar durchaus verschiedene Krümmungsmaße verwenden, aber ohne weitere Angabe würde ich die Begriffe "flach" oder "gekrümmt" immer auf den Riemann-Tensor beziehen. Und der ist in der Schwarzschild-Metrik natürlich nicht null. |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 14. Jan 2020 15:48 Titel: |
|
|
ok dann nochmal eine Frage zur Palatini-Identität.
ist dann:
oder
 |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 14. Jan 2020 19:34 Titel: |
|
|
| Corbi hat Folgendes geschrieben: | ok dann nochmal eine Frage zur Palatini-Identität.
ist dann:
oder
|
Im allgemeinen ersteres. Unter Umständen ist aber 
Das kommt darauf an wie die Variationen  definiert sind. Werden die Koordinaten mit variiert  ? Dann müßte im allgemeinen
gelten. |
|
|
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
| Corbi Verfasst am: 15. Jan 2020 13:26 Titel: |
|
|
Ich hab nicht ganz durchschaut wie man zu dem unteren Ausdruck kommt, also wenn auch die Koordinaten mitvariiert werden.
und noch ne andere Frage:
Ich hab grade noch den Energie-Impulstensor des E-M-Felds aus dem Wirkungsprinzip hergeleitet. Weißt du ob es auch eine Lagrange-Funktion gibt mit der man den Energie-Impuls-Tensor einer idealen Flüssigkeit erhält?[/quote] |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 15. Jan 2020 19:37 Titel: |
|
|
| Corbi hat Folgendes geschrieben: | Ich hab nicht ganz durchschaut wie man zu dem unteren Ausdruck kommt, also wenn auch die Koordinaten mitvariiert werden.
|
Das sollte sich aus der Definition
}{\partial (x^\mu + \delta x^\mu)},)
ergeben, wenn man nur die linearen Terme in und  behält.
Für eine mathematisch befriedigendere Behandlung dieser Variationen muß man Generatoren von sogenannten Kontakttransformationen auf Jet-Bündeln betrachten.
| Zitat: |
und noch ne andere Frage:
Ich hab grade noch den Energie-Impulstensor des E-M-Felds aus dem Wirkungsprinzip hergeleitet. Weißt du ob es auch eine Lagrange-Funktion gibt mit der man den Energie-Impuls-Tensor einer idealen Flüssigkeit erhält? |
Ja, über die Lagrangeformulierung des idealen Fluids steht glaube ich was in Hawking, Ellis, "The large scale structure of space-time". |
|
|
|
Registrieren
Login
FAQ
Suchen
