| Autor |
Nachricht |
gumgumpower
Anmeldungsdatum: 25.05.2019
Beiträge: 1
|
 gumgumpower Verfasst am: 25. Mai 2019 15:38 Titel: Euler-Lagrange-Gleichung , Extremalisierung eines Funktional gumgumpower Verfasst am: 25. Mai 2019 15:38 Titel: Euler-Lagrange-Gleichung , Extremalisierung eines Funktional |
 |
|
Meine Frage:
Moin moin,
In theoretischer Physik wurde folgende Aufgabe auf dem aktullen Übungszettel gestellt und ich habe da zurzeit überhaut keinen Ansatz. Bzw. Ich weiß aud irgendwie nicht, wie ich den ganzen Schmarn lesen muss.
Es sei ein Funktional der Form
,f(x)^{,},f(x)^{,,} \, \dd dx
<br />
)
das für Funktionen f
=a, f^{,}(x_l)=b,f(x_u)=c,f^{,}(x_u)=d
<br />
)
wobei a,b,c,d Konstanen sind, definiert ist. Zeigen Sie, dass die Euler-Lagrange-Gleichung für die Extremalisierung dieses Funktionals die Gestalt
-\frac{d}{dx}\frac{\partial G}{\partial {{f}'}}(x,\bar{f},\bar{{{f}'}},\bar{{{f}'}'})+\frac{\partial G}{\partial f}(x,\bar{f},\bar{{{f}'}},\bar{{{f}'}'})=0
<br />
)
hat.
Wäre nett wenn mir jemand einen Ansatz oder vielleicht sogar eine verständliche Lösung geben könnte.
Meine Ideen: |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 26. Mai 2019 12:21 Titel: Re: Euler-Lagrange-Gleichung , Extremalisierung eines Funkti Huggy Verfasst am: 26. Mai 2019 12:21 Titel: Re: Euler-Lagrange-Gleichung , Extremalisierung eines Funkti |
 |
|
| gumgumpower hat Folgendes geschrieben: | Meine Frage:
Ich weiß aud irgendwie nicht, wie ich den ganzen Schmarn lesen muss.
Es sei ein Funktional der Form
,f(x)^{,},f(x)^{,,} \, \dd dx
<br />
) |
Es ist gar nicht gut, wenn man eine Sache, mit der man sich beschäftigen soll, als Schmarrn bezeichnet. Was ist dir denn an diesem Ausdruck nicht klar? Man hat eine Funktion 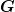 , die von , die von  und Funktionen und Funktionen ) und deren ersten beiden Ableitungen abhängt. Wenn man eine konkrete Funktion und deren ersten beiden Ableitungen abhängt. Wenn man eine konkrete Funktion 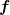 , die die gegebenen Randbdingungen erfüllt, einsetzt und das Integral ausführt, erhält man ein Ergebnis (eine Zahl) , die die gegebenen Randbdingungen erfüllt, einsetzt und das Integral ausführt, erhält man ein Ergebnis (eine Zahl)  . .  hängt offensichtlich von der gewählten Funktion hängt offensichtlich von der gewählten Funktion 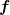 ab. Daher steht auf der linken Seite ab. Daher steht auf der linken Seite  . Gesucht ist nun diejenige Funktion . Gesucht ist nun diejenige Funktion 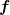 aus dem zulässigen Funktionenbereich, die aus dem zulässigen Funktionenbereich, die  maximiert oder minimiert. Diese Lösungsfunktion ist bei euch maximiert oder minimiert. Diese Lösungsfunktion ist bei euch 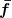 genannt. genannt.
Um die Euler-Lagrange-Gleichungen herzuleiten, kann man die Funktionen  schreiben als schreiben als

oder ausführlicher
=\bar f(x) + \epsilon g(x))
Damit 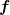 die Randbedingungen erfüllt, müssen die Funktionen die Randbedingungen erfüllt, müssen die Funktionen 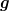 und deren erste Ableitung an den Rändern Null sein. Ansonsten sind sie beliebig aus dem zulässigen Funktionenbereich. Mit dieser Darstellung wird und deren erste Ableitung an den Rändern Null sein. Ansonsten sind sie beliebig aus dem zulässigen Funktionenbereich. Mit dieser Darstellung wird  eine Funktion des Parameters eine Funktion des Parameters  . Da . Da 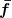 die Lösungsfunktion sein soll, hat die Lösungsfunktion sein soll, hat  sein Maximum oder Minimum bei sein Maximum oder Minimum bei  . .
 ist eine ganz gewöhnliche Funktion und ihre Extremstellen können durch Nullsetzen der Ableitung gefunden werden. ist eine ganz gewöhnliche Funktion und ihre Extremstellen können durch Nullsetzen der Ableitung gefunden werden.

Die Ableitung kann in das Integral gezogen werden und man erhält für den Integranden nach der Kettenregel

mit

Im nächsten Schritt integriert man diejenigen Summanden im Integral, die  bzw. bzw.  enthalten ein- bzw. zweimal partiell. Dabei fallen die ausintegrierten Terme wegen der Randbedingung für enthalten ein- bzw. zweimal partiell. Dabei fallen die ausintegrierten Terme wegen der Randbedingung für 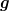 weg. Man erhält schließlich ein Ergebnis der Form weg. Man erhält schließlich ein Ergebnis der Form
g dx)
Da das Integral für beliebige Funktionen 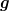 aus dem zulässigen Funktionenbereich Null werden soll. muss der Term aus dem zulässigen Funktionenbereich Null werden soll. muss der Term ) Null werden. Das sind die gesuchten Euler-Lagrange-Gleichungen. Null werden. Das sind die gesuchten Euler-Lagrange-Gleichungen. |
|
 |
|
|



