| Autor |
Nachricht |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 27. Nov 2016 21:58 Titel: Zustand eines Systems Max Cohen Verfasst am: 27. Nov 2016 21:58 Titel: Zustand eines Systems |
 |
|
Hallo zusammen, ich habe die Aufgabe:
Betrachte einen zweidimensionalen Hilbertraum mit ONB 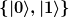 , sowie den Zustand: , sowie den Zustand:  und die Operatoren: und die Operatoren: 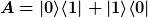 und und )
A werde im Zustand 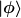 gemessen. Was sind die möglichen Messergebnisse und mit welchen Wahrscheinlichkeiten treten diese auf? gemessen. Was sind die möglichen Messergebnisse und mit welchen Wahrscheinlichkeiten treten diese auf?
Meine Idee:
Ich bin mir nich sicher wie die Ket Vektoren 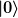 und und 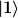 konkret ausschauen. Wenn ich das wüsste, könnte ich konkret ausschauen. Wenn ich das wüsste, könnte ich  erstmal als Matrix darstellen und die zugehörigen Eigenwerte bestimmen. Das Gleiche dann für B. Die Eigenvektoren müssten bei erstmal als Matrix darstellen und die zugehörigen Eigenwerte bestimmen. Das Gleiche dann für B. Die Eigenvektoren müssten bei  und bei B jeweils die ONB sein, stimmt das? und bei B jeweils die ONB sein, stimmt das?
Die Wahrscheinlichkeit wäre dann =|\langle\phi|0\rangle|^2) und und =|\langle\phi|1\rangle|^2)
Wobei 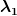 und und  Eigenwerte zum Operator Eigenwerte zum Operator  sind. sind.
Wäre das Vorgehen erstmal so korrekt?
Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18017
|
 TomS Verfasst am: 28. Nov 2016 07:03 Titel: TomS Verfasst am: 28. Nov 2016 07:03 Titel: |
 |
|
Du kannst eine Matrixdarstellung von
\,|\psi_\lambda\rangle = 0)
 = 0)
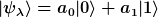
ableiten, indem du eine Projektion auf |0>, |1> durchführst; dazu musst du die Gleichungen "sandwichen":
 |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Nov 2016 11:29 Titel: index_razor Verfasst am: 28. Nov 2016 11:29 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Meine Idee:
Ich bin mir nich sicher wie die Ket Vektoren 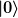 und und 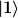 konkret ausschauen. konkret ausschauen.
|
Das schöne ist, es spielt keine Rolle. Du mußt nur wissen, daß sie orthogonal und normiert sind. Das ist genau der Grund warum Hilberträume so eine wichtige Abstraktion in der Quantenmechanik darstellen.
| Zitat: |
Wenn ich das wüsste, könnte ich  erstmal als Matrix darstellen und die zugehörigen Eigenwerte bestimmen. Das Gleiche dann für B. Die Eigenvektoren müssten bei erstmal als Matrix darstellen und die zugehörigen Eigenwerte bestimmen. Das Gleiche dann für B. Die Eigenvektoren müssten bei  und bei B jeweils die ONB sein, stimmt das? und bei B jeweils die ONB sein, stimmt das?
|
Nein, das gegebene ONS  besteht nicht aus Eigenvektoren der Operatoren A und B. Aber jeder Eigenvektor besteht nicht aus Eigenvektoren der Operatoren A und B. Aber jeder Eigenvektor 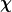 ist (so wie jeder Vektor überhaupt) eine Linearkombination der Elemente dieses ONS. Also muß gelten ist (so wie jeder Vektor überhaupt) eine Linearkombination der Elemente dieses ONS. Also muß gelten

Wende diesen Vektor z.B. auf den Operator A an und benutze, daß 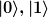 orthonormiert sind: orthonormiert sind:
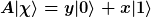
Jetzt fordere die Gültigkeit der Eigenwertgleichung 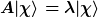 . .
Das ergibt
)
Was folgt daraus für  , x und y? , x und y? |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 28. Nov 2016 16:38 Titel: Max Cohen Verfasst am: 28. Nov 2016 16:38 Titel: |
 |
|
Hallo index_razor, ich hänge noch an der Darstellung von
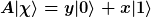
Wenn ich A und \chi einsetze erhalte ich: (x|0\rangle+y|1\rangle))
Ausmutipliziert ...
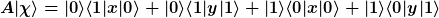
Wie darf hier weiter gerechnet werden?
Ich denke es läuft auf einen Koeffizientenvergleich herauß:
)
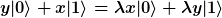
Also muss gelten:
 und und
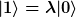
Macht das denn Sinn jetzt nach  aufzulösen? Ich meine dann würde man zwei Vektoren dividieren ... aufzulösen? Ich meine dann würde man zwei Vektoren dividieren ...
Viele Grüße! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Nov 2016 16:58 Titel: index_razor Verfasst am: 28. Nov 2016 16:58 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Hallo index_razor, ich hänge noch an der Darstellung von
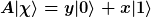
Wenn ich A und \chi einsetze erhalte ich: (x|0\rangle+y|1\rangle))
Ausmutipliziert ...
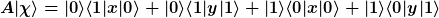
Wie darf hier weiter gerechnet werden?
|
x und y sind komplexe Zahlen. Die kannst du aus dem Hilbertraumprodukt ziehen. Also  etc. Dann benutzt du einfach die Orthogonalität und Normiertheit der Basisvektoren. etc. Dann benutzt du einfach die Orthogonalität und Normiertheit der Basisvektoren.
| Zitat: |
Ich denke es läuft auf einen Koeffizientenvergleich herauß:
)
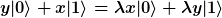
|
Koeffizientenvergleich ist schon das richtige Stichwort. Hier wird nun die Gleichheit zweier Linearkombinationen aus den beiden Basisvektoren 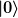 und und 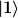 behauptet. Oder anders ausgedrückt: Es ergibt sich, daß die Linearkombination behauptet. Oder anders ausgedrückt: Es ergibt sich, daß die Linearkombination
|0\rangle+(x-\lambda y)|1\rangle=0)
gleich dem Nullvektor ist. Was folgt also damit aus der linearen Unabhängigkeit der Basisvektoren über die Koeffizienten in dieser Linearkombination? |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 28. Nov 2016 18:16 Titel: Max Cohen Verfasst am: 28. Nov 2016 18:16 Titel: |
 |
|
Hallo,
Wegen der Orthogonalität komme ich schonmal auf:

Nun kenne ich noch die Identität 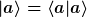
Damit müsste ich erhalten:

Wie bekomme ich das weiter vereinfacht?
Ich denke die Koeffizienten müssen Null sein da die Basisvektoren nicht Null werden können?
Dann hat man die Gleichungen:
I. 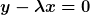
II. 
Damit erhalte ich die Eigenwerte: 
Für die Koeffizienten erhält man: Für 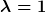 : :  und Für und Für  : : 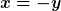
Damit lauten die Eigenvektoren zum jeweiligen Eigenwert:
)
)
Die möglichen Messergebnisse werden nun durch die Eigenwerte beschrieben oder?
Die Wahrscheinlichkeit berechnet sich dann mit =|\langle\chi|\phi\rangle|^2) und und
=|\langle\chi|\phi\rangle|^2)
So ist das gemeint?
Viele Grüße! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Nov 2016 20:17 Titel: index_razor Verfasst am: 28. Nov 2016 20:17 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Hallo,
Wegen der Orthogonalität komme ich schonmal auf:

Nun kenne ich noch die Identität 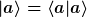
Damit müsste ich erhalten:

Wie bekomme ich das weiter vereinfacht?
|
Dir fehlen offenbar ein paar Grundlagen. Vorausgesetzt war, daß es sich bei  um eine Orthonormalbasis handelt. Das bedeutet es gilt paarweise um eine Orthonormalbasis handelt. Das bedeutet es gilt paarweise 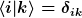 . .  ist hier das Hilbertraumprodukt. Dies ist, wie das Skalarprodukt von Vektoren in der Euklidischen Geometrie, eine Zahl. Anders als in der Euklidischen Geometrie handelt es sich aber i.a. um eine komplexe Zahl und die Vertauschung von ist hier das Hilbertraumprodukt. Dies ist, wie das Skalarprodukt von Vektoren in der Euklidischen Geometrie, eine Zahl. Anders als in der Euklidischen Geometrie handelt es sich aber i.a. um eine komplexe Zahl und die Vertauschung von 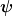 und und  ergibt das Komplex-konjugierte: ergibt das Komplex-konjugierte: 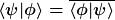 . Ansonsten ist nicht viel anders. . Ansonsten ist nicht viel anders.
Die Bedeutung dieses Produkts ergibt sich aus der physikalischen Interpretation als Wahrscheinlichkeitsamplituden für Meßergebnisse: Ist 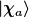 der Zustand, in dem mit Sicherheit der (nichtentartete) Meßwert der Zustand, in dem mit Sicherheit der (nichtentartete) Meßwert  irgendeiner Observable gemessen wird, so ist irgendeiner Observable gemessen wird, so ist 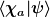 die Amplitude der Wahrscheinlichkeit im Zustand die Amplitude der Wahrscheinlichkeit im Zustand 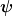 genau diesen Meßwert genau diesen Meßwert  zu messen, d.h. die Wahrscheinlichkeit selbst ist das Betragsquadrat dieses Zahlenwertes. zu messen, d.h. die Wahrscheinlichkeit selbst ist das Betragsquadrat dieses Zahlenwertes.
Eine Gleichung wie  ist demzufolge sinnlos. Links steht ein Vektor und rechts sein Hilbertraumprodukt mit sich selbst, also eine Zahl. ist demzufolge sinnlos. Links steht ein Vektor und rechts sein Hilbertraumprodukt mit sich selbst, also eine Zahl.
Operatoren wie A und B, sind lineare Abbildungen auf dem Hilberraum, die, auf Vektoren angewendet, wiederum Vektoren ergeben, d.h. es muß gelten
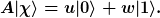
für irgendwelche Koeffizienten  . Auf keinen Fall ist das Ergebnis eine Linearkombination aus Produkten . Auf keinen Fall ist das Ergebnis eine Linearkombination aus Produkten  . Wie sieht das Ergebnis . Wie sieht das Ergebnis 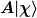 nun im allgemeinen aus? nun im allgemeinen aus?
Jeder Operator hat in unserem 2-dimensionalen Hilbertraum eine Basisdarstellung der Form

Die Zahlen  sind genau die Koeffizienten der Matrixdarstellung von A bzgl. der Basis sind genau die Koeffizienten der Matrixdarstellung von A bzgl. der Basis  . Die . Die 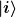 numerieren dabei die Zeilen, die numerieren dabei die Zeilen, die 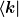 die Spalten. Kommt, wie beim Operator die Spalten. Kommt, wie beim Operator  , ein Term nicht vor, so ist das entsprechende Matrixelement null. Wendet man nun A auf , ein Term nicht vor, so ist das entsprechende Matrixelement null. Wendet man nun A auf  an, so ergibt sich nach Auswertung aller Skalarprodukte mit Hilfe von an, so ergibt sich nach Auswertung aller Skalarprodukte mit Hilfe von  : :

Zusammenfassen und Koeffizientenvergleich liefert

und
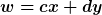
Oder
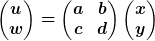
| Zitat: |
Ich denke die Koeffizienten müssen Null sein da die Basisvektoren nicht Null werden können?
|
Die Koeffizienten müssen null sein, ja. Nur deine Begründung ist etwas schief. Wie lautet die Bedingung für lineare Unabhängigkeit? Mehr als diese Definition vorbeten, muß man hier nicht tun, um die Behauptung zu rechtfertigen.
| Zitat: |
Dann hat man die Gleichungen:
I. 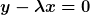
II. 
Damit erhalte ich die Eigenwerte: 
Für die Koeffizienten erhält man: Für 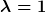 : :  und Für und Für  : : 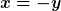
Damit lauten die Eigenvektoren zum jeweiligen Eigenwert:
)
)
Die möglichen Messergebnisse werden nun durch die Eigenwerte beschrieben oder?
|
Ja. Nun mußt du noch berücksichtigen, daß die Eigenvektoren, als physikalische Zustände, auf 1 normiert sein müssen, d.h. 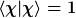 . Was folgt daraus? . Was folgt daraus?
| Zitat: |
Die Wahrscheinlichkeit berechnet sich dann mit =|\langle\chi|\phi\rangle|^2) und und
=|\langle\chi|\phi\rangle|^2)
|
Genau. Was kommt denn raus?
(Edit: Latex repariert.)
Zuletzt bearbeitet von index_razor am 03. Nov 2018 10:40, insgesamt einmal bearbeitet |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 28. Nov 2016 21:10 Titel: Max Cohen Verfasst am: 28. Nov 2016 21:10 Titel: |
 |
|
Hallo, danke schonmal für deinen Beitrag. Die Länge eines Kets ist 
Wenn ich meinen Eigenvektor normieren möchte muss ich meinen EV mit dem Kehrwert von  multiplizieren. multiplizieren.
Ein Eigenvektor lautet 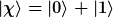

Ich weiß ehrlich gesagt nicht wie ich das nun auswerten soll ... Wenn es Vektoren wären die man für gewöhnlich benutzt wäre es klar. Hier ist das aber anders. Wie soll ich das machen wenn ich nicht die Komponenten des Eigenvektors kenne?
Viele Grüße |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Nov 2016 21:21 Titel: index_razor Verfasst am: 28. Nov 2016 21:21 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Ein Eigenvektor lautet 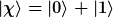

Ich weiß ehrlich gesagt nicht wie ich das nun auswerten soll ... Wenn es Vektoren wären die man für gewöhnlich benutzt wäre es klar. Hier ist das aber anders. Wie soll ich das machen wenn ich nicht die Komponenten des Eigenvektors kenne?
|
Nein, hier ist überhaupt nichts anders. Es handelt sich um gewöhnliche Vektoren in einem komplexen Vektorraum. Oben hattest du bereits die Eigenvektoren bestimmt:
)
Deren Komponenten bzgl. der Basis  mußt du hier nur noch ablesen. mußt du hier nur noch ablesen.
Multipliziere doch einfach mal
)
mit sich selbst. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 28. Nov 2016 21:34 Titel: Max Cohen Verfasst am: 28. Nov 2016 21:34 Titel: |
 |
|
Wenn mir ein Vektor der Form  gegeben ist dann ist mir klar was zu tun ist. Warum hat man den Vektor nicht in der Form gegeben sondern aufgeteilt in zwei Ket Vektoren? gegeben ist dann ist mir klar was zu tun ist. Warum hat man den Vektor nicht in der Form gegeben sondern aufgeteilt in zwei Ket Vektoren?
)
)
Für den anderen Eigenvektor läuft die Rechnung analog ...
Viele Grüße! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Nov 2016 22:09 Titel: index_razor Verfasst am: 28. Nov 2016 22:09 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Wenn mir ein Vektor der Form  gegeben ist dann ist mir klar was zu tun ist. Warum hat man den Vektor nicht in der Form gegeben sondern aufgeteilt in zwei Ket Vektoren? gegeben ist dann ist mir klar was zu tun ist. Warum hat man den Vektor nicht in der Form gegeben sondern aufgeteilt in zwei Ket Vektoren?
|

Dies besagt nichts anderes, als daß
 und und 
jeweils die Koeffizientenmatrizen der Basisvektoren  bzgl. der durch sie selbst gebildeten Basis darstellen. bzgl. der durch sie selbst gebildeten Basis darstellen.
| Zitat: |
)
)
|
Das Normquadrat ist das Produkt aus dem "Ket" 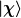 und dem zugehörigen "Bra" und dem zugehörigen "Bra"  . Bei der Bildung des letzteren mußt du beachten, alle Koeffizienten durch ihre komplex-konjugierten zu ersetzen, also . Bei der Bildung des letzteren mußt du beachten, alle Koeffizienten durch ihre komplex-konjugierten zu ersetzen, also
.)
Was kommt dann raus? Was ist insbesondere 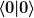 und und 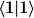 ? ? |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 28. Nov 2016 22:31 Titel: Max Cohen Verfasst am: 28. Nov 2016 22:31 Titel: |
 |
|
Ok, jetzt wird mir einiges klar. Für die Normierung gilt dann erstmal:
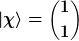
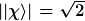 ... Damit lautet die Normierung für die Eigenvektoren: ... Damit lautet die Normierung für die Eigenvektoren:
)
)
Das x wäre demnach nur ein streckung oder stauchungsfaktor des Vektors.
Die Wahrscheinlichkeiten lauten somit:
=|\langle\chi|\phi\rangle|^2=|\langle\frac{1}{\sqrt{2}}\binom{1}{1}|\binom{1/\sqrt{10}}{3/ \sqrt{10}}\rangle|^2=|\binom{\frac{1}{\sqrt{20}}}{\frac{3}{\sqrt{20}}}|^2=\frac{4}{20}=\frac{1}{5})
Da die Wahrscheinlichkeit 1 ergeben muss gilt =\frac{4}{5})
Ich hoffe das passt nun.
Viele Grüße!  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Nov 2016 08:03 Titel: index_razor Verfasst am: 29. Nov 2016 08:03 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Das x wäre demnach nur ein streckung oder stauchungsfaktor des Vektors.
|
Nicht ganz, aber fast. Gehen wir noch mal schrittweise vor. Die Normierungsbedingung für  ) liefert liefert
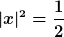 , ,
d.h. x ist bis auf einen Faktor vom Betrag 1 gleich 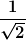 . Im Komplexen kann ein solcher Faktor die Form . Im Komplexen kann ein solcher Faktor die Form 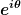 mit einem beliebigen Phasenwinkel mit einem beliebigen Phasenwinkel 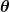 haben. Es gilt also haben. Es gilt also
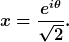
Der Faktor x bestimmt also nicht nur die Norm, sondern auch die globale Phase des Vektors 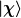 . Genauer als auf diese unbekannte Phase kannst du den Eigenvektor, oder jeden Vektor, aus physikalischer Sicht nicht bestimmen. Denn jede globale Phase ist physikalisch ohne Konsequenzen, da sie aus den Übergangswahrscheinlichkeiten herausfällt. Aus diesem Grunde sagt man auch, daß physikalische Zustände durch Strahlen im Hilbertraum definiert sind. Ein "Strahl" ist dabei eine Menge normierter Vektoren, die sich nur um eine Phase unterscheiden. Die Annahme . Genauer als auf diese unbekannte Phase kannst du den Eigenvektor, oder jeden Vektor, aus physikalischer Sicht nicht bestimmen. Denn jede globale Phase ist physikalisch ohne Konsequenzen, da sie aus den Übergangswahrscheinlichkeiten herausfällt. Aus diesem Grunde sagt man auch, daß physikalische Zustände durch Strahlen im Hilbertraum definiert sind. Ein "Strahl" ist dabei eine Menge normierter Vektoren, die sich nur um eine Phase unterscheiden. Die Annahme 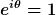 ist also eine legitime Festsetzung, mit der du einen Vertreter oder "Repräsentanten" aus diesem Strahl willkürlich auswählst. ist also eine legitime Festsetzung, mit der du einen Vertreter oder "Repräsentanten" aus diesem Strahl willkürlich auswählst.
| Zitat: |
Die Wahrscheinlichkeiten lauten somit:
=|\langle\chi|\phi\rangle|^2=|\frac{1}{\sqrt{2}}\binom{1}{1}|\binom{1/\sqrt{10}}{3/ \sqrt{10}}|^2=|\binom{\frac{1}{\sqrt{20}}}{\frac{3}{\sqrt{20}}}|^2=\frac{4}{20}=\frac{1}{5})
|
Nein. Die Übergangsamplitude für
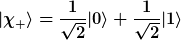
im Zustand
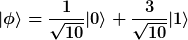
ist
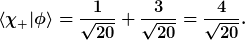
Also ist die Übergangswahrscheinlichkeit
=|\langle \chi_+|\phi\rangle|^2=\frac{4}{5}.
<br />
)
Irgendwie hast du es geschafft die beiden Werte für  zu vertauschen. Der Fehler kommt wohl nach dem dritten '=' von rechts. Es sieht so aus als hättest du die beiden Vektoren komponentenweise multipliziert. Dieser Schritt ergibt keinen Sinn. zu vertauschen. Der Fehler kommt wohl nach dem dritten '=' von rechts. Es sieht so aus als hättest du die beiden Vektoren komponentenweise multipliziert. Dieser Schritt ergibt keinen Sinn.
Versuchen wir es nochmal für den anderen Operator B? Sollte ja jetzt vielleicht ein bißchen leichter gehen. Ich würde dir auch empfehlen nochmal ein bißchen lineare Algebra aufzufrischen. Es scheint da ein paar Lücken zu geben. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 29. Nov 2016 14:47 Titel: Max Cohen Verfasst am: 29. Nov 2016 14:47 Titel: |
 |
|
Hallo, ich habe nochmal alles soweit durchgerechnet und sollte mir nun auch klar sein. Jetzt der nächste Aufgabenteil.
b) Würde man nun direkt noch einmal A messen mit welcher Wahrscheinlichkeit ergäbe sich welches Ergebnis angenommen bei der ersten Messung hat man den größtmöglichen Messwert erhalten?
Der größtmögliche Messwert ist damit die Wahrscheinlichkeit zum Eigenvektor  gemeint oder ist der größtmögliche Messwert in dem Fall der Eigenwert gemeint oder ist der größtmögliche Messwert in dem Fall der Eigenwert  ? ?
Dann müsste ich dieses mal auswerten: =|\langle\chi|\chi_1\rangle|^2) wobei wobei ) und dann wieder die Wahrscheinlichkeit für beide Eigenwerte ausrechnen. und dann wieder die Wahrscheinlichkeit für beide Eigenwerte ausrechnen.
=|(\frac{1}{\sqrt{2}}~\frac{1}{\sqrt{2}})\binom{1/\sqrt{2}}{1/\sqrt{2}}|^2=1)
Damit müsste dann =0) sein. sein.
Ist das überhaupt so gemeint?
Viele Grüße! |
|
 |
|
















