| Autor |
Nachricht |
Rudi92
Gast
|
 Rudi92 Verfasst am: 26. Nov 2016 15:00 Titel: Funktionalableitung Rudi92 Verfasst am: 26. Nov 2016 15:00 Titel: Funktionalableitung |
 |
|
Meine Frage:
Hallo,
Ich stehe total auf dem Schlauch was Funktionalableitungen angeht. Es ist ja eigentlich wie ne ganz normale Ableitung, nur das man eben ein Funktional nach einer Funktion ableitet. Wir haben aus der VL folgende Definition gegeben:
} = \text{lim}_{\epsilon->0} \frac{F[\phi(x)+\epsilon \delta(x-x_0)]-F[\phi(x)]}{\epsilon})
Jetz sei z.B.: ^2)
Ich verstehe einfach nicht, wie ich das Funktional in die Definition zur Funktionalableitung einzusetzen habe, da F von  abhängt und man jetzt F gleich abhängt und man jetzt F gleich  setzt. setzt.
Meine Ideen:
Ich erwarte eigentlich, dass irgendetwas wie ) rauskommt. rauskommt.
Allerdings kommt ich da so nicht hin:
} = \text{lim}_{\epsilon->0} \frac{\phi(x)^2+\epsilon\delta(x-x_0)-\phi(x)^2}{\epsilon}=\delta(x-x_0))
Ich hab hier irgendwo einen Denkfehler. Ich möchte keine Lösung, sondern nur einmal ausformuliert wie das korrekt eingesetzt wird. In der VL steht bei den Beispiel einfach immer direkt ein Ergebnis und ich sehe es nicht -.-' |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 26. Nov 2016 18:07 Titel: Re: Funktionalableitung TomS Verfasst am: 26. Nov 2016 18:07 Titel: Re: Funktionalableitung |
 |
|
| Rudi92 hat Folgendes geschrieben: | Jetzt sei z.B.
^2) |
Ich denke, dich verwirrt die Definition des Funktionals. Setze z.B.
\,u(y))
Dann ist
} = n\,\phi^{n-1}(x)\,u(x))
Wenn du stattdessen formal ohne Integrale bzw. mit der delta-Distribution rechnen möchtest, dann kannst du
}{\delta \phi(x)} = \delta(x-y))
verwenden.
Diese Ableitung tritt dann jedoch im Integral von F auf, so dass die Integration über dy wieder eine Funktion von x liefert.
Allgemein: ein Funktional F ordnet einer Funktion phi eine (komplexe) Zahl zu. Ein Funktional ist also etwas anderes als eine Funktion. Häufig treten bei der Definition Integrale auf. In diesem Sinne ist dann auch das delta-Funktional als spezielles Funktional zu verstehen: unter dem Integral steht die delta-Distribution als Integralkern und projiziert den Wert der Funktion phi an der Stelle a heraus; damit ordnet sie der gesamten Funktion phi genau eine Zahl, nämlich den Funktionswert an der Stelle a zu:
\,\phi(y) = \phi(a)) |
|
 |
Rudi92
Gast
|
 Rudi92 Verfasst am: 26. Nov 2016 18:39 Titel: Re: Funktionalableitung Rudi92 Verfasst am: 26. Nov 2016 18:39 Titel: Re: Funktionalableitung |
 |
|
| TomS hat Folgendes geschrieben: |
Ich denke, dich verwirrt die Definition des Funktionals. Setze z.B.
\,u(y)) |
Kann ich das einfach so machen? Ich meine mein Funktional ist doch klar vorgegeben.
Ich hab nochmal versucht mit der Definition zu arbeiten und komme mit L'hospital auf folgendes:
} = \text{lim}_{\epsilon->0} \frac{\phi^2[x+\epsilon \delta(x-x_0)]-\phi^2[x]}{\epsilon}=2\phi(x)\delta(x-x_0))
Was ja dem entspricht was du gesagt hast.
| TomS hat Folgendes geschrieben: |
} = n\,\phi^{n-1}(x)\,u(x))
|
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Nov 2016 20:16 Titel: index_razor Verfasst am: 26. Nov 2016 20:16 Titel: |
 |
|
| Rudi92 hat Folgendes geschrieben: | Meine Frage:
Hallo,
Ich stehe total auf dem Schlauch was Funktionalableitungen angeht. |
Darüber mußt du dir wohl nicht weiter den Kopf zerbrechen. Eure Definition läßt m.E. einiges an Klarheit vermissen. Es gibt verschiedene Verallgemeinerungen der aus dem endlichedimensionalen bekannten Ableitungsbegriffe. Die Frechet-Ableitung ist eine Verallgemeinerung des totalen Differentials auf beliebige vollständige normierte Räume, die Gateaux-Ableitung eine Verallgemeinerung der Richtungsableitung. Eine davon ist höchstwahrscheinlich gemeint.
Ich denke mit der Frechet-Ableitung kommt man als Physiker für die meisten Anwendungen wie z.B. der Variationsrechnung aus. Zumindest würde ich sagen, ist der Begriff für das von dir betrachtete Funktional
^2)
vollkommen ausreichend, ohne daß man sich dabei irgendwie mit  -Distributionen verrenken muß. Von der Frage, was die punktweise Addition einer Funktion -Distributionen verrenken muß. Von der Frage, was die punktweise Addition einer Funktion  mit der "Deltafunktion", wie in mit der "Deltafunktion", wie in +\epsilon\delta(y-x)) überhaupt bedeuten soll, kann man dann ohne weiteres absehen. (Das erscheint mir auch überhaupt nicht so offensichtlich zu sein.) überhaupt bedeuten soll, kann man dann ohne weiteres absehen. (Das erscheint mir auch überhaupt nicht so offensichtlich zu sein.)
In diesem Sinne (Frechet) ist die "Ableitung von  nach nach  " nichts anderes als der lineare Term der Änderung von F in " nichts anderes als der lineare Term der Änderung von F in  , d.h. um die Ableitung (das Differential) zu bestimmen, berechnest du also , d.h. um die Ableitung (das Differential) zu bestimmen, berechnest du also

Die ... müssen irgendeinen Term ergeben, der mindestens quadratisch von  abhängt. Und der lineare, stetige (!) Operator A, sofern er existiert, ist die "Funktionalableitung" von F nach abhängt. Und der lineare, stetige (!) Operator A, sofern er existiert, ist die "Funktionalableitung" von F nach  . .
Angewendet auf ^2) bedeutet dies bedeutet dies
(x)]^2=\phi(x)^2 +2\phi(x)\eta(x)+\eta(x)^2= F[\phi]+2\phi(x)\eta(x)+\eta(x)^2.)
An dieser Stelle muß man wahrscheinlich genauer definieren, von welcher Norm auf dem fraglichen Funktionenraum man spricht. Ist z.B.  die Supremumsnorm, so wäre die Supremumsnorm, so wäre
^2|}{\|\eta\|}\leq \frac{\|\eta\|^2}{\|\eta\|}=\|\eta\|\to 0)
für  , was die Differenzierbarkeit von F beweist und zeigt, daß dessen Differential an der "Stelle" , was die Differenzierbarkeit von F beweist und zeigt, daß dessen Differential an der "Stelle"  gleich gleich
)
ist, d.h. es handelt sich um die lineare Abbildung  , die jedem , die jedem  aus dem betrachteten Funktionenraum den Wert aus dem betrachteten Funktionenraum den Wert
\eta(x))
zuordnet, wie du auch schon vermutet hast. |
|
 |
Rudi92
Gast
|
 Rudi92 Verfasst am: 27. Nov 2016 12:40 Titel: Rudi92 Verfasst am: 27. Nov 2016 12:40 Titel: |
 |
|
|
Wow, vielen Dank! Deine Bemerkungen muss ich mir jetzt erstmal in Ruhe durchdenken. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 27. Nov 2016 16:39 Titel: Re: Funktionalableitung TomS Verfasst am: 27. Nov 2016 16:39 Titel: Re: Funktionalableitung |
 |
|
| Rudi92 hat Folgendes geschrieben: | | ... mein Funktional ist doch klar vorgegeben. |
Na ja, es ist halt kein Funktional :-)
Nach Wikipedia:
Als Funktional bezeichnet man in der Mathematik zumeist eine Funktion aus einem Vektorraum V in den Körper, der dem Vektorraum zugrunde liegt. Oft ist V ein Funktionenraum, also ein Vektorraum, dessen Elemente reell- oder komplexwertige Funktionen sind. Ein Funktional ist somit eine Funktion auf Funktionen ... Wir beschränken uns hier fast ausschließlich auf Fälle, in denen der Zahlenkörper der Körper der reellen oder komplexen Zahlen ist.
Ein Funktional F ordnet einer Funktion f also eine Zahl c zu: F[f] = c.
Deine Abbildung ordnet der Funktion phi jedoch die Funktion phi^2 zu. Demnach handelt es sich hierbei schlichtweg nicht um ein Funktional. Das solltest du klären. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Nov 2016 17:54 Titel: Re: Funktionalableitung index_razor Verfasst am: 27. Nov 2016 17:54 Titel: Re: Funktionalableitung |
 |
|
| TomS hat Folgendes geschrieben: |
Deine Abbildung ordnet der Funktion phi jedoch die Funktion phi^2 zu. Demnach handelt es sich hierbei schlichtweg nicht um ein Funktional. Das solltest du klären. |
Meine Vermutung war, daß es sich um das Funktional handelt, welches jeder Funktion  das Quadrat ihres Funktionswertes an der festen Stelle x zuordnet. das Quadrat ihres Funktionswertes an der festen Stelle x zuordnet.
Wäre  eine Funktion, hätte da ja eigentlich eine Funktion, hätte da ja eigentlich  = \phi(x)^2) stehen müssen. stehen müssen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 27. Nov 2016 20:24 Titel: Re: Funktionalableitung TomS Verfasst am: 27. Nov 2016 20:24 Titel: Re: Funktionalableitung |
 |
|
| index_razor hat Folgendes geschrieben: | Wäre  eine Funktion, hätte da ja eigentlich eine Funktion, hätte da ja eigentlich  = \phi(x)^2) stehen müssen. stehen müssen. |
Aber genau das steht da ja:
| Rudi92 hat Folgendes geschrieben: | Jetzt sei z.B.: ^2) |
Deswegen bringt es nichts, wenn wir beide vermuten, welches Funktional gemeint sein könnte. Erst muss die Definition klar sein. |
|
 |
Gast__
Gast
|
 Gast__ Verfasst am: 30. Apr 2020 19:52 Titel: Gast__ Verfasst am: 30. Apr 2020 19:52 Titel: |
 |
|
Hallo, ich klinke mich mal ein, weil ich auch eine Frage zur Funktionalableitung habe.
Und zwar haben wir die folgende Definition bekommen:
]}{\delta \phi(\vec{r})}\eta (\vec{r}) d^{d}r )
Ich bin nicht sicher wie ich an ]}{\delta \phi(\vec{r})} ) rankomme, weil ich mit dem rankomme, weil ich mit dem 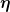 absolut nichts anfangen kann. Wir haben dazu keine Erklärung bekommen. absolut nichts anfangen kann. Wir haben dazu keine Erklärung bekommen.
Kann mir jemand sagen, was genau 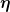 ist? ist? |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 30. Apr 2020 21:46 Titel: Nils Hoppenstedt Verfasst am: 30. Apr 2020 21:46 Titel: |
 |
|
| Gast__ hat Folgendes geschrieben: |
]}{\delta \phi(\vec{r})}\eta (\vec{r}) d^{d}r )
Ich bin nicht sicher wie ich an ]}{\delta \phi(\vec{r})} ) rankomme, weil ich mit dem rankomme, weil ich mit dem 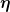 absolut nichts anfangen kann. absolut nichts anfangen kann. |
Du liest die Definition verkehrt rum: der rechte Ausdruck wird über den linken Ausdruck definiert, nicht umgekehrt. D.h. du erhältst die Funktionalableitung, indem du den Term
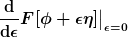
auswertest. Das  ist dabei eine beliebige Testfunktion. Das Funktional, das sich dabei am Ende ergibt, muss natürlich unabhängig von der Testfunktion sein. ist dabei eine beliebige Testfunktion. Das Funktional, das sich dabei am Ende ergibt, muss natürlich unabhängig von der Testfunktion sein.
Hier ist ein schönes Beispiel vorgerechnet:
https://de.wikipedia.org/wiki/Funktionalableitung
Viele Grüße,
Nils |
|
 |
Gast__
Gast
|
 Gast__ Verfasst am: 01. Mai 2020 08:25 Titel: Gast__ Verfasst am: 01. Mai 2020 08:25 Titel: |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: |
D.h. du erhältst die Funktionalableitung, indem du den Term
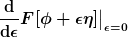
auswertest. Das  ist dabei eine beliebige Testfunktion. Das Funktional, das sich dabei am Ende ergibt, muss natürlich unabhängig von der Testfunktion sein. ist dabei eine beliebige Testfunktion. Das Funktional, das sich dabei am Ende ergibt, muss natürlich unabhängig von der Testfunktion sein.
|
Danke dir. D.h. wenn ich ein Funktional gegeben habe, muss ich "einfach"
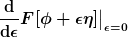 bilden und anhand dessen erkenne ich dann, was bilden und anhand dessen erkenne ich dann, was  ist, weil das Integral mit ist, weil das Integral mit  die gleiche Funktion ergeben muss? die gleiche Funktion ergeben muss? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Mai 2020 12:32 Titel: index_razor Verfasst am: 01. Mai 2020 12:32 Titel: |
 |
|
| Gast__ hat Folgendes geschrieben: | | Nils Hoppenstedt hat Folgendes geschrieben: |
D.h. du erhältst die Funktionalableitung, indem du den Term
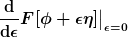
auswertest. Das  ist dabei eine beliebige Testfunktion. Das Funktional, das sich dabei am Ende ergibt, muss natürlich unabhängig von der Testfunktion sein. ist dabei eine beliebige Testfunktion. Das Funktional, das sich dabei am Ende ergibt, muss natürlich unabhängig von der Testfunktion sein.
|
Danke dir. D.h. wenn ich ein Funktional gegeben habe, muss ich "einfach"
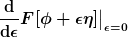 bilden und anhand dessen erkenne ich dann, was bilden und anhand dessen erkenne ich dann, was  ist, weil das Integral mit ist, weil das Integral mit  die gleiche Funktion ergeben muss? die gleiche Funktion ergeben muss? |
Leider nicht unbedingt. Die linke Seite von
}\eta (x)\dd x \qquad\text{(D)})
definiert so etwas wie die Richtungsableitung von F entlang  an der "Stelle" an der "Stelle"  . Die rechte Seite definiert ein Funktional, welches linear in . Die rechte Seite definiert ein Funktional, welches linear in  ist. ist.
Letzteres bezeichnet man in der gewöhnlichen Analysis als totales Differential oder einfach nur als Ableitung. Und wie in der gewöhnlichen Analysis garantiert die Existenz der Richtungsableitungen nicht die Differenzierbarkeit der Funktion und damit auch nicht die Existenz eines linearen Funktionals mit der Eigenschaft (D). Aus diesem Grund ist (D) m.E. keine gute Definition für die rechte Seite. Wenn allerdings die rechte Seite existiert, existiert auch die linke Seite und beide sind gleich. Das ist auch wie in der gewöhnlichen Analysis.
Wie du in der Praxis }) bestimmst, hängt sicher davon ab, in welcher Form F gegeben ist. In der Physik hat man es ja oft mit Funktionalen zu tun, die ebenfalls als Integrale über genügend glatte Funktionen gegeben sind (in welchem Fall die Differenzierbarkeit von F außer Frage steht), z.B. das Wirkungsfunktional bestimmst, hängt sicher davon ab, in welcher Form F gegeben ist. In der Physik hat man es ja oft mit Funktionalen zu tun, die ebenfalls als Integrale über genügend glatte Funktionen gegeben sind (in welchem Fall die Differenzierbarkeit von F außer Frage steht), z.B. das Wirkungsfunktional
\dd t.)
(Hier übernimmt jetzt  die Rolle von die Rolle von  aus den vorigen Formeln und aus den vorigen Formeln und  die Rolle von die Rolle von  .) In diesem Fall würde man einfach .) In diesem Fall würde man einfach ) bis zu Termen linear in bis zu Termen linear in  auswerten. Dieser lineare Term definiert die Funktionalableitung von S, d.h auswerten. Dieser lineare Term definiert die Funktionalableitung von S, d.h
 \eta + \frac{\dd}{\dd t}\left(\frac{\partial L}{\partial \dot x}\eta\right).)
Der letzte Term verschwindet natürlich bei der Integration, wenn, wie normalerweise, die möglichen Funktionen x vorgegebene Randwerte haben. In diesem Fall kann man also einfach schreiben
 |
|
 |
Gast__
Gast
|
 Gast__ Verfasst am: 03. Mai 2020 20:35 Titel: Gast__ Verfasst am: 03. Mai 2020 20:35 Titel: |
 |
|
@index_razor, wir sollen die Definition benutzen um für eine Reihe vorgegebener Funktionale die Funktionalableitung zu errechen. Daher kann man wohl davon ausgehen, dass die rechte Seite von (D) existiert.
Ich habe auch deine Antwort an Rudi gelesen, leider bin ich nicht gerade ine Mathe-Leuchte, ich verstehe das also nicht so hundertprozentig.
Was ich daraus nehme ist, dass die Funktionalableitung quasi Koeffizient der Taylorentwicklung von  im Term linear in im Term linear in 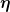 ist? ist?
Kann man das so sagen? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Mai 2020 21:46 Titel: index_razor Verfasst am: 03. Mai 2020 21:46 Titel: |
 |
|
| Gast__ hat Folgendes geschrieben: |
Was ich daraus nehme ist, dass die Funktionalableitung quasi Koeffizient der Taylorentwicklung von  im Term linear in im Term linear in 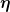 ist? ist?
Kann man das so sagen? |
Ja, so wie die normale Ableitung in der endlichdimensionalen Analysis ja eigentlich auch der lineare Term in dieser Entwicklung ist. |
|
 |
Gast__
Gast
|
 Gast__ Verfasst am: 04. Mai 2020 19:36 Titel: Gast__ Verfasst am: 04. Mai 2020 19:36 Titel: |
 |
|
Ach... ja natürlich, ich Rindvieh  Danke euch für eure Hilfe Danke euch für eure Hilfe  |
|
 |
Lissi27
Gast
|
 Lissi27 Verfasst am: 14. Jun 2020 10:13 Titel: Funktionalableitung Lissi27 Verfasst am: 14. Jun 2020 10:13 Titel: Funktionalableitung |
 |
|
Hallo zusammen,
dann klinke ich mich auch mal ein. Ich habe ein ähnliches Problem zu Funktionalableitungen. Und zwar habe ich Folgendes Funktional gegeben:
 = \int_{0}^{\infty} (f'(x))^2 \cdot x^5 dx. )
Mein Problem ist, dass das Funktional abhängig von f' und nicht von f ist.
Bei meiner Recherche bin ich auf Folgende Formel gekommen (steht auch bei Wikipedia):
) dx = -F''(f')f''. )
Ich hätte das jetzt einfach auf mein Funktional angewendet und erhalte als Funktionalableitung das hier:
 \cdot x^5. )
Dabei lasse ich  einfach als Konstante drin. Ist die Ableitung so korrekt? Müsste ich die noch durch 2 teilen, weil mein Integral nur von 0 beginnt und nicht über ganz R läuft? einfach als Konstante drin. Ist die Ableitung so korrekt? Müsste ich die noch durch 2 teilen, weil mein Integral nur von 0 beginnt und nicht über ganz R läuft? |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 14. Jun 2020 12:17 Titel: Re: Funktionalableitung Nils Hoppenstedt Verfasst am: 14. Jun 2020 12:17 Titel: Re: Funktionalableitung |
 |
|
| Lissi27 hat Folgendes geschrieben: | Und zwar habe ich Folgendes Funktional gegeben:
 = \int_{0}^{\infty} (f'(x))^2 \cdot x^5 dx. )
|
Das ist kein Funktional, sondern eine Funktion. Außerdem spielt x auf rechten Seite lediglich die Rolle der Integrationsvariablen, der Wert des Integrals selbst ist unabhängig von x. Es gilt also F(x) = const und damit F'(x) = 0.
Viele Grüße,
Nils |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Jun 2020 13:16 Titel: Re: Funktionalableitung index_razor Verfasst am: 14. Jun 2020 13:16 Titel: Re: Funktionalableitung |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | Lissi27 hat Folgendes geschrieben: | Und zwar habe ich Folgendes Funktional gegeben:
 = \int_{0}^{\infty} (f'(x))^2 \cdot x^5 dx. )
|
Das ist kein Funktional, sondern eine Funktion.
|
Doch, das ist ein Funktional von f. Da sollte allerdings wohl F(f) stehen und nicht F(x). Das ist vermutlich nur ein Tippfehler.
| Lissi27 hat Folgendes geschrieben: |
Ich hätte das jetzt einfach auf mein Funktional angewendet und erhalte als Funktionalableitung das hier:
 \cdot x^5. )
Dabei lasse ich  einfach als Konstante drin. Ist die Ableitung so korrekt? Müsste ich die noch durch 2 teilen, weil mein Integral nur von 0 beginnt und nicht über ganz R läuft? einfach als Konstante drin. Ist die Ableitung so korrekt? Müsste ich die noch durch 2 teilen, weil mein Integral nur von 0 beginnt und nicht über ganz R läuft? |
Als Ansatz würde ich immer  + \epsilon\eta(x)) in das gegebene F einsetzen und nach in das gegebene F einsetzen und nach  entwickeln. Da in diesem Fall F von entwickeln. Da in diesem Fall F von  abhängt, kommt die Ableitung abhängt, kommt die Ableitung  vor, die an der geeigneten Stelle gemäß der Produktregel abgewälzt werden muß. vor, die an der geeigneten Stelle gemäß der Produktregel abgewälzt werden muß.
Man erhält also
 = \int_0^\infty \dd x x^5 \left(f'^2(x) + 2f'(x)\epsilon \eta'(x) + \epsilon^2 \eta'^2(x)\right).)
Der erste Summand unter dem Integral ergibt wieder ) . Der Term linear in . Der Term linear in  enthält die Funktionalableitung.*) Allerdings muß das Integral in die Form enthält die Funktionalableitung.*) Allerdings muß das Integral in die Form
} \eta(x))
gebracht werden, wobei }) eine Funktion von x ist, die nicht mehr von eine Funktion von x ist, die nicht mehr von  ebhängt . Dafür mußt du die Produktregel verwenden ebhängt . Dafür mußt du die Produktregel verwenden
 \eta'(x) = \frac{\dd}{\dd x}\left(x^5 f'(x) \eta(x)\right) - \frac{\dd}{\dd x}\left(x^5 f'(x) \right) \eta(x).)
Jetzt mußt du nur noch erklären, was mit der totalen Ableitung nach x,
 \eta(x)\right),)
unter dem Integral passiert. Aus dem verbleibenden Integral kannst du die Funktionalableitung ablesen.
___________
*) Hier benutze ich, daß das Restintegral
 = \epsilon^2\int \dd x\ x^5\eta'^2(x))
die Eigenschaft |/|\epsilon| \to 0) für für  besitzt. Dies ist in der gewöhnlichen Analysis ausreichend um den linearen Term mit der Ableitung der Funktion zu identifizieren. besitzt. Dies ist in der gewöhnlichen Analysis ausreichend um den linearen Term mit der Ableitung der Funktion zu identifizieren.
Das ist streng genommen hier nicht ganz richtig. Korrekte wäre, zu verlangen, daß
/\|\eta\| \to 0) für für  . .
Für die Anwendung dieses Kriteriums ist die Aufgabe allerdings zu vage gestellt. Insbesondere ist der Definitionsbereich von F überhaupt nicht definiert worden und keine Norm  gegeben, mit der man die Funktionalableitung definieren könnte. Ich vermute deshalb, daß das heuristische Argument oben im Sinne der Aufgabenstellung ist. gegeben, mit der man die Funktionalableitung definieren könnte. Ich vermute deshalb, daß das heuristische Argument oben im Sinne der Aufgabenstellung ist. |
|
 |
Lissi27
Gast
|
 Lissi27 Verfasst am: 14. Jun 2020 15:17 Titel: Re: Funktionalableitung Lissi27 Verfasst am: 14. Jun 2020 15:17 Titel: Re: Funktionalableitung |
 |
|
Vielen Dank schon einmal für Ihre Antworten.
Ja, das war ein Tippfehler, es soll F(f) heißen. Mir ist noch nicht klar wieso man die Funktionalableitung so erhält:
| index_razor hat Folgendes geschrieben: |
Der Term linear in  enthält die Funktionalableitung. Allerdings muß das Integral in die Form enthält die Funktionalableitung. Allerdings muß das Integral in die Form
} \eta(x))
gebracht werden, wobei }) eine Funktion von x ist, die nicht mehr von eine Funktion von x ist, die nicht mehr von  ebhängt . ebhängt . |
Die Definition, die ich erhalten habe ist
}{\delta f} = \lim_{\epsilon \to 0} (\frac{F(f+\epsilon \eta) - F(f)}{\epsilon})) , ,
wobei
 = F(f) + \epsilon <\frac{\delta F(f)}{\delta f}, \eta>) für für  . Dafür muss . Dafür muss \subseteq supp(f)) . .
Dann ist meine erste Frage: Wo geht die Bedingung \subseteq supp(f)) ein? Ist das für die Existenz des Limes nötig? ein? Ist das für die Existenz des Limes nötig?
Und zweitens: Wie komme ich darauf, dass die Ableitung so zu finden ist, wie Sie es beschrieben haben, denn ich bekomme
}{\delta f} = \lim_{\epsilon \to 0}(\frac{\epsilon <\frac{\delta F(f)}{\delta f}, \eta> }{\epsilon}) = \int \frac{\delta F(f)}{\delta f} \eta. )
Und da stimmt doch dann irgendwas nicht, wenn links auch die Ableitung steht?
Ich kam damit dann bisher immer bis
}{\delta f} = \lim_{\epsilon \to 0} (\frac{F(f+\epsilon \eta) - F(f)}{\epsilon}) = \lim_{\epsilon \to 0} (\frac{\int (2f'(x)\epsilon \eta' + \epsilon^2 \eta'^2) \cdot x^5 dx}{\epsilon}) = \lim_{\epsilon \to 0} (\frac{\int 2f'(x)\epsilon \eta' x^5 dx}{\epsilon}))
und an der Stelle weiß ich noch nicht so recht weiter.
Warum ist die Funktionalableitung der Term vor  ? Was ist mit dem Integral und dem Nenner mit ? Was ist mit dem Integral und dem Nenner mit  ? ?
Viele Grüße,
Lis |
|
 |
Lissi27
Gast
|
 Lissi27 Verfasst am: 14. Jun 2020 16:12 Titel: Lissi27 Verfasst am: 14. Jun 2020 16:12 Titel: |
 |
|
Wenn ich mit ihrem Tipp weiter mache und jetzt mal annehme, dass ich die Ableitung in dem Integral } \eta(x)) erhalte, würde ich so vorgehen: erhalte, würde ich so vorgehen:
\epsilon \eta' x^5 dx}{\epsilon}) =\lim_{\epsilon \to 0} (\frac{2\epsilon \int \Big(\frac{d}{dx}(x^5 f' \eta) - \frac{d}{dx}(x^5f') \eta \Big)dx}{\epsilon} ) . Es ist noch gegeben, dass f eine . Es ist noch gegeben, dass f eine  Funktion ist. D.h Funktion ist. D.h
 dx = \Big[ x^5 f' \eta\Big]_{0}^{\infty} = 0 ) , mit , mit  , weil dann , weil dann  = 0) angenommen werden kann? angenommen werden kann?
Dann ist
 - \frac{d}{dx}(x^5f') \eta \Big)dx}{\epsilon} = \lim_{\epsilon \to 0} (\frac{2\epsilon \int \Big( - \frac{d}{dx}(x^5f') \eta \Big)dx}{\epsilon} = -2 \int \frac{d}{dx} (x^5 f') \eta dx = -2 \int (5x^4 f' + x^5 f'') \eta dx) . .
dann wäre die gesuchte Ableitung jetzt  ) ? ? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Jun 2020 16:49 Titel: Re: Funktionalableitung index_razor Verfasst am: 14. Jun 2020 16:49 Titel: Re: Funktionalableitung |
 |
|
| Lissi27 hat Folgendes geschrieben: | Vielen Dank schon einmal für Ihre Antworten.
Ja, das war ein Tippfehler, es soll F(f) heißen. Mir ist noch nicht klar wieso man die Funktionalableitung so erhält:
| index_razor hat Folgendes geschrieben: |
Der Term linear in  enthält die Funktionalableitung. Allerdings muß das Integral in die Form enthält die Funktionalableitung. Allerdings muß das Integral in die Form
} \eta(x))
gebracht werden, wobei }) eine Funktion von x ist, die nicht mehr von eine Funktion von x ist, die nicht mehr von  ebhängt . ebhängt . |
Die Definition, die ich erhalten habe ist
}{\delta f} = \lim_{\epsilon \to 0} (\frac{F(f+\epsilon \eta) - F(f)}{\epsilon})) , ,
|
Das kann nicht ganz stimmen. Der Grenzwert auf der rechten Seite wird im allgemeinen ja von  abhängen. Entscheidend ist aber, daß diese Abhängigkeit linear in abhängen. Entscheidend ist aber, daß diese Abhängigkeit linear in  ist. Links müßte also vermutlich ist. Links müßte also vermutlich

stehen. So wie in dieser Gleichung:
| Zitat: |
wobei
 = F(f) + \epsilon <\frac{\delta F(f)}{\delta f}, \eta>) für für  . .
|
Dann ist beides im wesentlichen dieselbe Bedingung.
| Zitat: |
Dafür muss \subseteq supp(f)) . .
Dann ist meine erste Frage: Wo geht die Bedingung \subseteq supp(f)) ein? Ist das für die Existenz des Limes nötig? ein? Ist das für die Existenz des Limes nötig?
|
Es wurde also festgelegt, daß 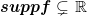 ? Ansonsten handelt es sich ja hier um keine Einschränkung an ? Ansonsten handelt es sich ja hier um keine Einschränkung an  . .
Falls ja, vermute ich, das soll sicherstellen, daß bestimmte Randterme \eta(x)|_0^\infty) verschwinden, die beim Abwälzen der Ableitung von verschwinden, die beim Abwälzen der Ableitung von  entstehen. Ansonsten fällt mir kein Grund für diese Bedingung ein. entstehen. Ansonsten fällt mir kein Grund für diese Bedingung ein.
| Zitat: |
Und zweitens: Wie komme ich darauf, dass die Ableitung so zu finden ist, wie Sie es beschrieben haben, denn ich bekomme
}{\delta f} = \lim_{\epsilon \to 0}(\frac{\epsilon <\frac{\delta F(f)}{\delta f}, \eta> }{\epsilon}) = \int \frac{\delta F(f)}{\delta f} \eta. )
Und da stimmt doch dann irgendwas nicht, wenn links auch die Ableitung steht?
|
Die Funktionalableitung }{\delta f}) ist ein linearer Operator auf irgendeinem Vektorraum von Funktionen f. Links steht die Anwendung dieses Operators auf die Funktion ist ein linearer Operator auf irgendeinem Vektorraum von Funktionen f. Links steht die Anwendung dieses Operators auf die Funktion  . Schreiben wir dafür mal kurz . Schreiben wir dafür mal kurz
 - F(f)).)
Die Anwendung dieses Operators }{\delta f}) schreibt man nun oft als Integral über eine verallgemeinerte Funktion (Distribution) -- nennen wir die mal schreibt man nun oft als Integral über eine verallgemeinerte Funktion (Distribution) -- nennen wir die mal ) -- multipliziert mit -- multipliziert mit  , d.h. , d.h.
\eta(x).)
Ich vermute das Integral auf der rechten Seite ist das, was ihr mit  bezeichnen würdet. Für den "Funktionswert" bezeichnen würdet. Für den "Funktionswert" ) schreibt man nun auch schreibt man nun auch
 = \frac{\delta F}{\delta f(x)})
und nennt dies ebenfalls Funktionalableitung. (Hauptsächlich Physiker tun das.) Damit hätten wir dann also folgende Identitäten
 - F(f)) = \frac{\delta F}{\delta f}.\eta = \langle F', \eta\rangle = \left\langle \frac{\delta F}{\delta f},\eta\right\rangle = \int_{-\infty}^\infty \dd x\ \frac{\delta F}{\delta f(x)}\eta(x))
Das wichtige an der Definition der Funktionalableitung ist aber, wie gesagt nur, daß der Grenzwert hier linear in  ist. ist.
| Zitat: |
Ich kam damit dann bisher immer bis
}{\delta f} = \lim_{\epsilon \to 0} (\frac{F(f+\epsilon \eta) - F(f)}{\epsilon}) = \lim_{\epsilon \to 0} (\frac{\int (2f'(x)\epsilon \eta' + \epsilon^2 \eta'^2) \cdot x^5 dx}{\epsilon}) = \lim_{\epsilon \to 0} (\frac{\int 2f'(x)\epsilon \eta' x^5 dx}{\epsilon}))
und an der Stelle weiß ich noch nicht so recht weiter.
|
Den Grenzwert ganz rechst kannst du trivial ausführen. Das ergibt
\epsilon \eta' x^5 dx)
Das ist linear in  , entspricht also , entspricht also /\delta f) angewendet auf angewendet auf  . Dies kannst du nun unter Berücksichtigung der gegebenen Bedingungen an . Dies kannst du nun unter Berücksichtigung der gegebenen Bedingungen an 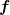 und und  als Integral über das Produkt aus als Integral über das Produkt aus  und und
}{\delta f(x)})
schreiben. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Jun 2020 17:10 Titel: index_razor Verfasst am: 14. Jun 2020 17:10 Titel: |
 |
|
| Lissi27 hat Folgendes geschrieben: | Es ist noch gegeben, dass f eine  Funktion ist. Funktion ist.
|
Es wäre hilfreich, wenn du diese Voraussetzungen von Anfang an dazu schreibst. Die stehen nicht umsonst in der Aufgabenstellung.
| Zitat: |
D.h
 dx = \Big[ x^5 f' \eta\Big]_{0}^{\infty} = 0 ) , mit , mit  , weil dann , weil dann  = 0) angenommen werden kann? angenommen werden kann?
|
Laut Voraussetzung ist ja sogar der Träger von  beschränkt, d.h. beschränkt, d.h.  \eta(x)) ist sicher null mit Ausnahme eines beschränkten Intervalls. ist sicher null mit Ausnahme eines beschränkten Intervalls.
| Zitat: |
Dann ist
 - \frac{d}{dx}(x^5f') \eta \Big)dx}{\epsilon} = \lim_{\epsilon \to 0} (\frac{2\epsilon \int \Big( - \frac{d}{dx}(x^5f') \eta \Big)dx}{\epsilon} = -2 \int \frac{d}{dx} (x^5 f') \eta dx = -2 \int (5x^4 f' + x^5 f'') \eta dx) . .
|
Warum schreibst du immer so umständlich diese Grenzwerte hin? Das  kürzt sich doch von Anfang an weg. kürzt sich doch von Anfang an weg.
| Zitat: |
dann wäre die gesuchte Ableitung jetzt  ) ? ? |
Es könnte sein, daß hier das Integral
}{\delta f(x)}\eta(x)\dd x)
zwischen  laufen soll. Dann fehlt noch die Multiplikation mit laufen soll. Dann fehlt noch die Multiplikation mit ) vor deinem Ergebnis. vor deinem Ergebnis.
Vielleicht solltest du nochmal den kompletten Aufgabentext wörtlich posten, damit klar ist, daß nicht noch irgendwelche wichtigen Voraussetzungen fehlen. |
|
 |
Lissi27
Gast
|
 Lissi27 Verfasst am: 14. Jun 2020 20:50 Titel: Lissi27 Verfasst am: 14. Jun 2020 20:50 Titel: |
 |
|
Vielen Dank für Ihre ausführliche Antwort! Jetzt habe ich die Funktionalableitung glaube ich richtig verstanden. Die Schreibweise hat mir nicht klar gemacht, dass das links die Anwendung auf den Operator ist, aber so macht es dann Sinn.
Die Aufgabenstellung ist: Gegeben sei das Funktional
 = \int_{0}^{\infty} (f'(x))^2 \cdot x^5 dx ) , ,
wobei  ) monoton fallend. monoton fallend.
Bestimmen Sie die Funktionalableitung.
| index_razor hat Folgendes geschrieben: |
Laut Voraussetzung ist ja sogar der Träger von  beschränkt, d.h. beschränkt, d.h.  \eta(x)) ist sicher null mit Ausnahme eines beschränkten Intervalls. ist sicher null mit Ausnahme eines beschränkten Intervalls.
|
Dass  bedeutet nur, dass f im Unendlichen verschwindet. Der Träger kann dabei trotzdem ganz bedeutet nur, dass f im Unendlichen verschwindet. Der Träger kann dabei trotzdem ganz  sein, oder nicht? Aber wir können sagen, dass die Ableitung im Grenzwert gegen 0 geht, und damit fällt der Term im Grenzwert auch weg, korrekt? sein, oder nicht? Aber wir können sagen, dass die Ableitung im Grenzwert gegen 0 geht, und damit fällt der Term im Grenzwert auch weg, korrekt?
| index_razor hat Folgendes geschrieben: |
Es könnte sein, daß hier das Integral
}{\delta f(x)}\eta(x)\dd x)
zwischen  laufen soll. Dann fehlt noch die Multiplikation mit laufen soll. Dann fehlt noch die Multiplikation mit ) vor deinem Ergebnis. vor deinem Ergebnis.
|
Das ist hier aber nicht der Fall, weil  ) nur für positive Argumente definiert ist, oder? nur für positive Argumente definiert ist, oder?
Sorry, dass ich die Bedingung nicht am Anfang mit hingeschrieben habe, hätte natürlich Sinn ergeben. Das merke ich mir für's nächste Mal...
Also würden Sie mir dann bei  ) als Ableitung zustimmen? als Ableitung zustimmen? |
|
 |
Lissi27
Gast
|
 Lissi27 Verfasst am: 14. Jun 2020 20:53 Titel: Lissi27 Verfasst am: 14. Jun 2020 20:53 Titel: |
 |
|
Kleine Korrektur:
 ) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Jun 2020 13:26 Titel: index_razor Verfasst am: 15. Jun 2020 13:26 Titel: |
 |
|
| Lissi27 hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: |
Laut Voraussetzung ist ja sogar der Träger von  beschränkt, d.h. beschränkt, d.h.  \eta(x)) ist sicher null mit Ausnahme eines beschränkten Intervalls. ist sicher null mit Ausnahme eines beschränkten Intervalls.
|
Dass  bedeutet nur, dass f im Unendlichen verschwindet. Der Träger kann dabei trotzdem ganz bedeutet nur, dass f im Unendlichen verschwindet. Der Träger kann dabei trotzdem ganz  sein, oder nicht? sein, oder nicht?
|
Hm, also ich kenne ) nur als Bezeichnung für eine Menge von beliebig oft differenzierbaren Funktionen mit kompaktem Träger. Wenn der Träger ganz nur als Bezeichnung für eine Menge von beliebig oft differenzierbaren Funktionen mit kompaktem Träger. Wenn der Träger ganz  sein kann, dann ist ja auch die Bedingung sein kann, dann ist ja auch die Bedingung \subseteq \text{supp}(f)) ohne Inhalt. ohne Inhalt.
| Zitat: |
Aber wir können sagen, dass die Ableitung im Grenzwert gegen 0 geht, und damit fällt der Term im Grenzwert auch weg, korrekt?
|
Warum können wir das sagen? Mir leuchtet das auf Anhieb nicht ein. (Was nicht heißt, daß es nicht stimmt.)
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Es könnte sein, daß hier das Integral
}{\delta f(x)}\eta(x)\dd x)
zwischen  laufen soll. Dann fehlt noch die Multiplikation mit laufen soll. Dann fehlt noch die Multiplikation mit ) vor deinem Ergebnis. vor deinem Ergebnis.
|
Das ist hier aber nicht der Fall, weil  ) nur für positive Argumente definiert ist, oder? nur für positive Argumente definiert ist, oder?
|
Ja, dann ergibt dein Ergebnis Sinn. |
|
 |
Lissi27
Gast
|
 Lissi27 Verfasst am: 15. Jun 2020 14:50 Titel: Lissi27 Verfasst am: 15. Jun 2020 14:50 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Warum können wir das sagen? Mir leuchtet das auf Anhieb nicht ein. (Was nicht heißt, daß es nicht stimmt.)
|
Also wir hatten C_0 Funktionen so, dass sie im Unendlichen verschwinden. Deshalb ist ja =0 ) und damit auch und damit auch =0 ) , für , für  monoton fallend. monoton fallend.
Aber du hast Recht, da bleibt noch das Problem, dass  gegen Unendlich geht und wir dann nicht sagen können, dass das Produkt gegen Null läuft... gegen Unendlich geht und wir dann nicht sagen können, dass das Produkt gegen Null läuft... |
|
 |
Matthias In
Gast
|
 Matthias In Verfasst am: 16. Jun 2020 11:56 Titel: Matthias In Verfasst am: 16. Jun 2020 11:56 Titel: |
 |
|
| Lissi27 hat Folgendes geschrieben: | Es ist noch gegeben, dass f eine  Funktion ist. D.h Funktion ist. D.h
 dx = \Big[ x^5 f' \eta\Big]_{0}^{\infty} = 0 ) , mit , mit  , weil dann , weil dann  = 0) angenommen werden kann? angenommen werden kann?
|
Ich stehe gerade vor fast dem gleichen Problem. Vorallem, es kann ja sein, dass  "schneller" wächst, als die "schneller" wächst, als die  Funktion und eta fallen. Dann würde alles gegen Unendlich gehen. Dann macht ja aber die ganze Ableitung keinen Sinn, wenn man als Ableitung dann sowas bekommt: Funktion und eta fallen. Dann würde alles gegen Unendlich gehen. Dann macht ja aber die ganze Ableitung keinen Sinn, wenn man als Ableitung dann sowas bekommt:
 = \infty) . .
Also, falls da jemand helfen kann, wäre ich auch an einer Lösung interessiert. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Jun 2020 13:14 Titel: index_razor Verfasst am: 16. Jun 2020 13:14 Titel: |
 |
|
Das Problem existiert doch schon bei der Definition von F. Offensichtlich reicht es nicht, daß f im Unendlichen gegen null geht. Es muß mindestens schneller verschwinden als 1/x², ansonsten kann
 = \int_0^\infty f'(x)^2x^5 \dd x)
ja auch schon divergieren.
Andererseits wissen wir ja
 - F(f) = 2\epsilon \int_0^\infty f'(x)\eta'(x)x^5\dd x + \epsilon^2 F(\eta).)
Damit ist nach Definition
\eta'(x)x^5\dd x)
Damit ist die Funktionalableitung eindeutig definiert, sofern das Integral auf der rechten Seite für alle "geeigneten"  exisitiert. Welche exisitiert. Welche  "geeignet" sind, hängt allerdings wieder vom Definitionsbereich von F ab, über den wir m.E. im Augenblick nicht genügend wissen. "geeignet" sind, hängt allerdings wieder vom Definitionsbereich von F ab, über den wir m.E. im Augenblick nicht genügend wissen.
Vielleicht hilft noch folgende Überlegung: Wenn der Definitionsbereich von F ein linearer Raum ist, dann gilt offensichtlich
 - F(f) - F(\eta))
Man benötigt also in diesem Fall für die Funktionalableitung nicht mehr Forderungen an f als bereits für die Definition von F. |
|
 |
|
|




 Danke euch für eure Hilfe
Danke euch für eure Hilfe 