| Autor |
Nachricht |
HaraldK
Anmeldungsdatum: 02.10.2012
Beiträge: 54
|
 HaraldK Verfasst am: 15. Nov 2012 20:47 Titel: Das Photon in der Kiste HaraldK Verfasst am: 15. Nov 2012 20:47 Titel: Das Photon in der Kiste |
 |
|
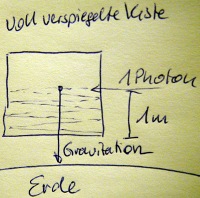
Ich habe eine würfelförmige Kiste mit ideal parallelen Seiten, die innen voll verspiegelt ist, während ich von außen Licht hinein senden kann (halbdurchlässiger Spiegel).
Nun schicke ich 1 m oberhalb des Kistenbodens ein einzelnes Photon in die Kiste und zwar mit Eintrittswinkel von exakt 90 Grad. (Siehe Grafik). Der Winkel soll so genau 90 Grad sein, dass das Photon bis in alle Ewigkeit zwischen den beiden Seitenwänden hin und her gespiegelt wird --- würde man die Gravitation vernachlässigen.
Die Gravitation führt dazu, dass der Weg des Photons ein klein wenig nach unten gebogen ist.
Frage: wie lange dauert es, bis das Photon auf dem Boden der Kiste ankommt?
Vermutung: man kann nun rumrechnen, wie lange das Photon jeweils quer durch die Kiste benötigt und wie weit es dabei nach unten abgelenkt wird. Ich aber denke, die Antwort lautet: es dauert 0,32s, genau so lange, wie es dauert, dass ein Ei (oder welcher Gegenstand auch immer) benötigt um auf der Erde 1m tief zu fallen, wenn er keinen Luftwiderstand spürt.
Andere Meinungen, Rechnungen, Überlegungen?
| Beschreibung: |
|
| Dateigröße: |
31.68 KB |
| Angeschaut: |
3757 mal |
|
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Nov 2012 00:21 Titel: TomS Verfasst am: 16. Nov 2012 00:21 Titel: |
 |
|
m.E. kannst du das Problem mittels Newtonscher Mechanik nicht lösen, da diese die Gravitation nur für Körper mit Ruhemasse ungleich Null formulieren kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
HaraldK
Anmeldungsdatum: 02.10.2012
Beiträge: 54
|
 HaraldK Verfasst am: 16. Nov 2012 07:49 Titel: HaraldK Verfasst am: 16. Nov 2012 07:49 Titel: |
 |
|
Ich habe nicht gesagt, dass ich das per Newtonscher Mechanik lösen will. Und das Gravitationsgesetz in der ART ist numerisch in diesem Problem wohl weitgehend identisch mit Newonscher Mechanik.
Mit ART gilt die Erdbeschleunigung dann für jede Art von Energie, auch für das Photon.
Dementsprechend gehe ich davon aus, dass das Photon wie alle Masse oder Energie mit 9,81m/s^2 Richtung Erdmittelpunkt beschleunigt wird. Das bedeutet es legt die 1 m Strecke bis zum Kistenboden in 0,32 Sekunden zurück.
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 16. Nov 2012 08:16 Titel: jh8979 Verfasst am: 16. Nov 2012 08:16 Titel: |
 |
|
Nimmt man das Aequivalenzprinzip ernst, "faellt" das Photon wohl genauso wie jeder andere Gegenstand (siehe zB Fahrstuhlbeispiel). Ich hab allerdings gerade keine Zeit das mal korrekt durchzurechnen, aber denke im Falle schwacher Gravitation sollte das rauskommen.
Davon abgesehen benoetigt ein Gegenstand auf der Erde im Vakuum keine 0.32s um 1m zu fallen.
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 16. Nov 2012 08:17 Titel: jh8979 Verfasst am: 16. Nov 2012 08:17 Titel: |
 |
|
Nimmt man das Aequivalenzprinzip ernst, "faellt" das Photon wohl genauso wie jeder andere Gegenstand (siehe zB Fahrstuhlbeispiel). Ich hab allerdings gerade keine Zeit das mal korrekt durchzurechnen, aber denke im Falle schwacher Gravitation sollte das rauskommen.
Davon abgesehen benoetigt ein Gegenstand auf der Erde im Vakuum keine 0.32s um 1m zu fallen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Nov 2012 08:19 Titel: TomS Verfasst am: 16. Nov 2012 08:19 Titel: |
 |
|
Gemäß der allgemeinen Relativitätstheorie erhält man für den Winkel der Ablenkung (berechnet für die Lichtablenkung im Gravitationsfeld eines Sternes) den doppelten Wert wie aus der Newtonschen Theorie; letztere macht hier also explizit falsche Vorhersagen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 16. Nov 2012 08:23 Titel: jh8979 Verfasst am: 16. Nov 2012 08:23 Titel: |
 |
|
Ich weiss... aber erstens hat man es hier ja mit einem konstanten Feld zu tun und keinem kugelsymmetrischen und keine Ablenkung im Unendlichen... und zweitens bin ich mit nem Ergebnis mit Faktor 2 Fehler ganz zufrieden 
PS: Was ist denn Dein Argument gegen die Aequivalenz mit einem konstant beschleunigten Fahrstuhl? Mir faellt da spontan kein gutes Gegenargument ein .. aber ART ist auch nicht direkt mein Fachgebiet...
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 16. Nov 2012 08:56 Titel: TomS Verfasst am: 16. Nov 2012 08:56 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Ich weiss... aber erstens hat man es hier ja mit einem konstanten Feld zu tun und keinem kugelsymmetrischen und keine Ablenkung im Unendlichen... und zweitens bin ich mit nem Ergebnis mit Faktor 2 Fehler ganz zufrieden :) |
Es geht mir ja nur darum, dass die Newtonsche Mechanik bzgl. der Bewegung von Photonen in der Newtonschen Mechanik explizit falsche Vorhersagen macht. Es mag sein, dass sie in Teilbereichen sogar richtige Vorhersagen macht, aber das ist dann Zufall!
Nehmen wir an, dass man mittels Äquivalenzprinzip argumentieren könnte und dass das richtige Ergebnis für die Fallzeit herauskommt. Trotzdem wissen wir, dass für die Bahnkurve (ihre Geometrie) selbst explizit etwas Falsches herauskommt. Was nützt uns dann das ganze Ergebnis für die Falldauer?
Wenn dir dein Bankberater sagt, dass Anlage A 15% Zinsen abwirft (was dir niemand außer ihm sagen kann) und dass Anlage B sogar 20% Zinsen abwirft (wobei dir die Börsenstatistik sagt, dass in der Realität ein Verlust von -10% zu Buche schlägt!), würdest du in Anlage A investieren??
| jh8979 hat Folgendes geschrieben: | | PS: Was ist denn Dein Argument gegen die Aequivalenz mit einem konstant beschleunigten Fahrstuhl? Mir faellt da spontan kein gutes Gegenargument ein .. aber ART ist auch nicht direkt mein Fachgebiet... |
Das Äquivalenzprinzip besagt (mathematisch formuliert), dass sich Körper unabhängig von ihrer Masse auf denselben Geodäten bewegen. Allerdings ist eine konkrete Geodäte immer durch die Anfangsbedingungen, also Ort und Geschwindigkeit ausgezeichnet. Und bzgl. der Geschwindigkeit haben wir einen wesentlichen Unterschied: Das massebehaftete Teilchen wird entlang seiner Geodäte explizit schneller, das masselose Teilchen wird nicht schneller sondern bewegt sich immer mit konstanter Geschwindigkeit c. Umgekehrt könnte man argumentieren dass sich die Horizontalgeschwindigkeit des massebehafteten Teilchens nicht ändert, während seine Vertikalgeschwindigkeit zunimmt, während sich beim Photon die Horizontalgeschwindigkeit ändern muss (sie muss sich verringern), damit die Vertikalgeschwindigkeit überhaupt zunehmen kann (so dass der Betrag weiterhin konstant gleich c bleibt). Daraus folgt, dass die naive Anwendung der Formeln v = gt und h = h° - gt ½ gt² nicht zulässig sein kann.
Es gibt also explizit zwei unterschiedliche Klassen von Geodäten, zeitartige und lichtartige, und ich bin mir nicht sicher, dass man die Argumente für zeitartige Geodäten (für massebehaftete Teichen) auf lichtartige (für masselose Teilchen)= übertragen kann.
Aber genug geschwätzt; ich werde das halt mal ausrechnen ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 16. Nov 2012 09:10 Titel: jh8979 Verfasst am: 16. Nov 2012 09:10 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Es gibt also explizit zwei unterschiedliche Klassen von Geodäten, zeitartige und lichtartige, und ich bin mir nicht sicher, dass man die Argumente für zeitartige Geodäten (für massebehaftete Teichen) auf lichtartige (für masselose Teilchen)= übertragen kann. |
Ich mir auch nicht... genau genommen hab ich wie Du das Gefuehl, dass da vermutlich etwas falsch laufen könnte  ... ...
Andererseits ist es meist moeglich den Limes m->0 zu nehmen, *wenn* man denn vorsichtig ist... und im Fahrstuhlbeispiel seh ich nicht ganz, wo die Masse auftaucht (das Beispiel der Ablenkung am Stern oder so ist anders, da das Feld dort nicht homogen ist).
|
|
 |
hhkk
Gast
|
 hhkk Verfasst am: 16. Nov 2012 16:49 Titel: hhkk Verfasst am: 16. Nov 2012 16:49 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Umgekehrt könnte man argumentieren dass sich die Horizontalgeschwindigkeit des massebehafteten Teilchens nicht ändert, während seine Vertikalgeschwindigkeit zunimmt, während sich beim Photon die Horizontalgeschwindigkeit ändern muss (sie muss sich verringern), damit die Vertikalgeschwindigkeit überhaupt zunehmen kann (so dass der Betrag weiterhin konstant gleich c bleibt). Daraus folgt, dass die naive Anwendung der Formeln v = gt und h = h° - gt ½ gt² nicht zulässig sein kann.
|
An der Stelle finde ich es interessant zu erwähnen, dass durch einfache Umstellung der SRT-Gleichungen folgt
^2)
wobei  die lokale Zeit ist, die so eine Art Alterungsgeschwindigkeit ist. Die Gleichung gilt immer, unabhängig von der Ruhemasse. Soviel zum Thema, dass sich bei massebehafteten Teilchen die Geschwindigkeit ändert. Eigentlich wird nur umgeschichtet von "altern" in "bewegen" :-) die lokale Zeit ist, die so eine Art Alterungsgeschwindigkeit ist. Die Gleichung gilt immer, unabhängig von der Ruhemasse. Soviel zum Thema, dass sich bei massebehafteten Teilchen die Geschwindigkeit ändert. Eigentlich wird nur umgeschichtet von "altern" in "bewegen" :-)
Aber ich will Dich nicht bei Deiner Berechnung verwirren. Ich bin nämlich wirklich gespannt, was herauskommt. Kann die Gravitation voll wirken und die "waagerechte" Bewegung des Photons "wegbremsen", oder klappt das wegbremsen nicht komplett und die Beschleunigung des Photons Richtung Erde ist etwas langsamer als  erwarten lassen? erwarten lassen?
|
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 16. Nov 2012 18:00 Titel: D2 Verfasst am: 16. Nov 2012 18:00 Titel: |
 |
|
Wenn ich auch etwas sagen darf.
Die Aufgabe errinert mich an diese Scherzfrage:
http://www.physikerboard.de/htopic,30464,hund.html
Man kann nur spekulieren wie lange es in einer h= 1 m Vakuumkiste dauern wird bis das Photon auf den Boden ankommt, aber wenn es 2 Photonen sein sollen, dann kann man diese mit einem Elektronen- Positronen Paar ersetzen
http://de.wikipedia.org/wiki/Annihilation
Die Idee ist einfach. Schwerpunkt Kiste/Teilchenpaar wird durch die Gravitation beeinflusst, unabhängig davon ob die Teilchen annihilieren oder nicht.
Wie lange wird es daueren bis die Teilchen mit dem Vertikalimpuls Null brauchen werden um auf dem Boden anzukommen?
Unabhängig von der Masse oder Teilchen/Antiteilchenenart
t = Wurzel(2 * h / g)
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
 |
HaraldK
Anmeldungsdatum: 02.10.2012
Beiträge: 54
|
 HaraldK Verfasst am: 17. Nov 2012 08:52 Titel: HaraldK Verfasst am: 17. Nov 2012 08:52 Titel: |
 |
|
| D2 hat Folgendes geschrieben: | Wie lange wird es daueren bis die Teilchen mit dem Vertikalimpuls Null brauchen werden um auf dem Boden anzukommen?
Unabhängig von der Masse oder Teilchen/Antiteilchenenart
t = Wurzel(2 * h / g) |
Also doch ganz einfach das Gravitationsgesetz anwenden, egal in welcher Form die Masse/Energie auch vorliegt. In meiner Rechnung hatte ich allerdings den Faktor 2 schlicht vergessen, so dass also im konkreten Fall herauskommt:

|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 18. Nov 2012 01:51 Titel: TomS Verfasst am: 18. Nov 2012 01:51 Titel: |
 |
|
Ich betrachte mal den allgemeineren Fall eines inhomogenen Gravitationsfeldes, speziell die (stationäre) Schwarzschildlösung im Außenraum einer kugelsymmetrischen Massenverteilung. Die gewählten Koordinaten sind (t,r); die Winkelkoordinaten (θ,φ) sind im Folgenden irrelevant; eine Näherung für ein (näherungsweise) homogenen Gravitationsfeld erhält man durch r = R+x mit R = const. und x/R << 1.
Zunächst führe ich die zwei Funktionen
 = \left( \kappa + \frac{L^2}{r^2} \right))
 = \left( 1 - \frac{2M}{r} \right))
Dabei gilt κ=1 für massebehaftete Teilchen m>0 und κ=0 für masselose Teilchen m=0.
Der Zusammenhang zwischen Eigenzeit τ (bzw. affinem Parameter s für masselose Teilchen) und Koordinatenzeit t lautet

Die Energiegleichung lautet
^2 = E^2 - f_{\kappa,L}(r)\, h(r) )
Da wir einen Vergleich zwischen massebehafteten und masselosen Teilchen durchführen wollen können wir nicht die Eigenzeit benutzen (da diese für masselose Teilchen nicht definiert ist) sondern formulieren das Problem stattdessen in Koordinatenzeit, d.h.
^2 = \left(\frac{dr}{dt} \, \frac{dt}{d\tau}\right)^2 = \left(\frac{dr}{dt} \, \frac{E}{h}\right)^2 )
Daraus folgt
}\right)^2 = E^2 - f_{\kappa,L}(r)\, h(r) )
Auflösen nach dt liefert

und damit für die Zeitdifferenz für das Zurücklegen der Differenz im Radius von r nach r – Δr

Da nun aber die beiden Integranden für m=0 mit κ=0 sowie m>0 und κ=1 strukturell unterschiedlich sind, wird auch (bei gleicher Energie E) die Zeitdifferenz (in Koordinatenzeit) Δt i.A. unterschiedlich sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 18. Nov 2012 02:11 Titel: TomS Verfasst am: 18. Nov 2012 02:11 Titel: |
 |
|
Die Newtonsche Näherung für m>0 erhält man, wenn man in h den Grenzübergang
 \to 1)
durchführt.
Der Fall m=0 kann allerdings aus der Newtonschen Mechanik nicht hergeleitet werden
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
HaraldK
Anmeldungsdatum: 02.10.2012
Beiträge: 54
|
 HaraldK Verfasst am: 18. Nov 2012 13:55 Titel: HaraldK Verfasst am: 18. Nov 2012 13:55 Titel: |
 |
|
Vielen Dank für die ausführliche Herleitung. Da ich nicht Physik studiert habe, sondern mich der Materie nur mit mathematischen Vorkenntnissen aber Unwissen über Formelzeichenkonventionen annähere, kann ich mit etwa der Hälfte der Variablen leider nichts anfangen.
Ich weiß, dass das saulästig ist, aber wenn Du die Variablen R, L, 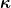 , M, , M, ) und h (ohne Parameter) erklären würdest, könnte man Deine Herleitung sicher verstehen. So ist das ganze leider nur für Eingeweihte zu verstehen. Aber die würden nicht fragen. und h (ohne Parameter) erklären würdest, könnte man Deine Herleitung sicher verstehen. So ist das ganze leider nur für Eingeweihte zu verstehen. Aber die würden nicht fragen.
Wie lange braucht den nun das Photon, bis es auf dem Boden der Kiste angelangt ist?
(P.S. Die Verwendung vieler Variablen ohne Erklärung der Bedeutung und Signatur ist leider auch in teuren Physiklehrbüchern weit verbreitet und führt gerade für jemand der sich einlesen will nicht gerade zur Erhellung.)
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 18. Nov 2012 14:19 Titel: TomS Verfasst am: 18. Nov 2012 14:19 Titel: |
 |
|
OK; ich werde das nochmal einfacher darstellen, insbs. werde ich das für ein konstantes Gravitationsfeld mit der potentiellen Energie U = mgz (m = Masse, g = "Erdbeschleunigung", z = z-.Koordinate = Höhe) herleiten. Außerdem kann man gleichermaßen annehmen, dass man es mit einer beschleunigten Bewegung der Kiste mit Beschleunigung g zu tun hat. Damit sollte die Äquivalenz von Beschleunigung g und (homogenem) Gravitationsfeld mit "Erdbeschleunigung" g klar werden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
HaraldK
Anmeldungsdatum: 02.10.2012
Beiträge: 54
|
 HaraldK Verfasst am: 18. Nov 2012 14:27 Titel: HaraldK Verfasst am: 18. Nov 2012 14:27 Titel: |
 |
|
Hoffe mein Einwand zu den Variablen ist nicht zu heftig rüber gekommen. Ich kann verstehen, dass man nicht gleich eine Veröffentlichung schreiben will. Aber ich habe wirklich schon so oft über Physikbücher geflucht, dass ich da wohl auch etwas sensibel bin 
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 18. Nov 2012 14:43 Titel: TomS Verfasst am: 18. Nov 2012 14:43 Titel: |
 |
|
Nun, mir ging es auch gar nicht um die Einzelheiten, sondern um den strukturellen Unterschied zwischen lichtartigen Teilchen und massebehafteten Teilchen.
Zu den Bedeutungen:
M: Masse des Zentralkörpers (z.B. Erde)
L: Drehimpuls (erhalten entlang einer Bahnkurve
E: eine Konstante der Bewegung, verwandt mit der rel. Gesamtenergie (genauer Bezug spielt keine Rolle)
κ=1,0: wiord verwendet, um in der selben Formel die verschiedenen Fälle m>0 und m=0 behandeln zu können.
f,h: zwei Funktionen
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2012 08:40 Titel: TomS Verfasst am: 20. Nov 2012 08:40 Titel: |
 |
|
push - hab's nicht vergessen
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 25. Nov 2012 15:24 Titel: TomS Verfasst am: 25. Nov 2012 15:24 Titel: |
 |
|
Hallo nochmal, hoffe, das Thema ist noch von Interesse: es geht um den Vergleich eines im Schwerfeld fallenden (massiven) Teilchens und um ein (masseloses) Photon.
Wir betrachten drei verschiedene Situationen, nämlich A) einen gravitationsfreien Raum (Minkowski-Raum) mit einem konstant beschleunigten Kasten sowie B) einen kugelsymmetrischen Himmelskörper mit Schwarzschildmetrik. Ich werde die wesentlichen Unterschiede aufzeigen. Zuletzt komme ich noch auf einige exotische Beispiele C) zurück, die bzgl. des Gravitationsfeldes dem Fall A) ähneln, jedoch bzgl. des Falls von Probekörpern eher Effekte wie bei B) aufweisen
A) entspricht dem ursprünglichen Gedankenexperiment Einsteins. Interessanterweise ist die exakte mathematische Behandlung bereits ziemlich kompliziert. Man benötigt dazu die sogenannten Rindler-Koordinaten
http://en.wikipedia.org/wiki/Rindler_coordinates
Man startet für mit einer Bahnkurve in flachen Minkowski-Koordinaten
 = (T,X=A,0,vT))
Diese Bahnkurve sieht der nicht-beschleunigte Beobachter, d.h. er misst seine Zeit T, der Wert X sei konstant gleich A, der Wert Y konstant gleich 0, und in Z-Richtung bewegt sich das Teilchen mit einer Geschwindigkeit v ≤ 1 (ich setze c=1).
Der in x-Richtung beschleunigte Beobachter benutzt sogenannte Rindler-Koordinaten. Diese haben die interessante Eigenschaft, dass sie einen Ereignishorizont für T = ±X enthalten und somit nur in einem Teilbereich des Minkowski-Raumes gültig sind. In diese Koordinaten lautet die Bahnkurve
 = (t,x,y,z) = \left( \frac{1}{g}\text{artanh}\left( \frac{T}{A} \right),\sqrt{A^2-T^2},0,vT\right))
noch ausgedrückt durch die Minkowski-Zeit T. Uns interessiert aber nur, dass die neue x-Koordinate unabhängig von der Geschwindigkeit v gewählt wird. Das bedeutet nun folgendes:
Teilchen beliebiger Geschwindigkeit v ≤ 1 legen in der selben Zeit t die selbe Strecke x (jeweils gemessen in Rindler-Koordinaten) zurück. D.h. ein massebehaftete Teilchen m > 0 „fällt“ aus der Ruhelage genauso schnell wie ein ursprünglich in Z-Richtung bewegtes Photon mit Z=vT (das Photon bewegt sich am Start rein in z-Richtung, wird aber natürlich für t>0 durch die Beschleunigung auch eine Bewegung in x-Richtung aufweisen)
Aufgrund des Ereignishorizontes können wir nicht berechnen, wie lange es (in Rindler-Koordinaten) dauert, bis das Teilchen von der Anfangsposition x=A zu x=0 gefallen ist (da hier das Koordinatensystem singulär wird). Wir können aber natürlich berechnen, wie lange es dauert, bis das Teilchen von x = A bis x = A - h für sehr kleines h fällt.
B) Nun zur Schwarzschildmetrik:
http://en.wikipedia.org/wiki/Schwarzschild_coordinates
Hier betrachten wir zunächst den radialen Fall eines Testteilchens, das sich ursprünglich in Ruhe befindet. Die Dauer des Falls (mit Fallhöhe h) von einem Radius r zu r-h berechnet sich zu

Die Gleichung gilt für die Koordinatenzeit t außerhalb des Schwarzschildhorizontes. Die Falldauer zum Schwarzschildhorizont selbst ist Unendlich, da in diesem Fall der Nenner Null wird und der Logarithmus divergiert!
Im Falle eines massiven Teilchens kann man auch die in dessen Eigenzeit gemessene Falldauer berechnen; man findet auch für den Fall bis zum Schwarzschildradius die endliche Zeit

D.h. dass für einen außenstehenden Beobachter der Fall bis zum Ereignishorizont unendlich lange zu dauern scheint, dass der Fall für das Teilchen selbst jedoch in endlicher Zeit stattfindet (für normale Himmelskörper befindet sich der Schwarzschildradius im Inneren und die Rechnungen sind nur gültig für den Fall bis zu dessen Oberfläche).
Nun vergleichen wir das mit dem Fall eines zunächst rein tangential bewegten Lichtstrahls. Tangential bedeutet, dass der Lichtstrahl (zunächst) keine radiale Geschwindigkeitskomponente besitzt. Er kann aber im Gegensatz zu dem massiven Teilchen natürlich nicht vollständig in Ruhe sein (für das Teilchen habe ich angenommen, dass es am Radius r zunächst ruht).
Ich hatte das oben bereits skizziert, möchte hier aber auf die eher komplizierte Rechnung verzichten und statt dessen ein ganz einfache Überlegung anstellen: Wir wissen, dass Lichtstrahlen an Sternen leicht abgelenkt werden, d.h. wir vermuten, dass rein tangentiale Lichtstrahlen sozusagen in Richtung des Sternes „fallen“. Wir überlegen uns, wie das in der Nähe eines schwarzen Lochs aussehen könnte. Dort stellt man nämlich fest, dass bei

ein (instabiler) kreisförmiger Orbit für Photonen möglich ist. D.h. hier gilt gemessen in Koordinatenzeit t

Für unser Photon in der Kiste bedeutet dies nun folgendes: Stellen wir uns vor, der Beobachter befindet sich innerhalb einer stationären Kiste auf Höhe des Photonorbits (recht nahe am Schwarzschildradius). Er lässt zum einen ein massives Teilchen aus der Ruhelage senkrecht fallen und misst die Zeitdauer, die es zum Zurücklegen einer Strecke h benötigt. Zum anderen beobachtet er einen Lichtstrahl senkrecht zur Wirkung des Gravitationsfeldes; für letzteren stellt er fest, dass dieser rein tangential verläuft, d.h. es findet (bei nicht zu großer Kiste) keinerlei Ablenkung statt!
Dies ist nun nicht weiter verwunderlich, denn der Beobachter befindet sich ja eben nicht in einem konstanten Gravitationsfeld sondern in einem Gravitationsfeld eines extrem kompakten Sternes oder sogar eines schwarzen Lochs. Und zudem führt der Beobachter ein nicht-lokales Experiment durch: für eine genügend große Kiste würde er feststellen, dass die Photonen einer Kreisbahn folgen und dass die Bahnen frei fallende Testteilchen in Richtung des Kistenbodens aufeinander zulaufen.
C) Nun kann man versuchen, andere Gravitationsfelder zu konstruieren, die (im Gegensatz zur Schwarzschildmetrik) eine reine x-abhängige „Kraftkomponente“ haben. Beispiele dafür sind die Gravitationsfelder unendlich ausgedehnter sowie infinitesimal dünner Platten in der yz-Ebene (wodurch eine Anziehungskraft in x-Richtung zustande kommen sollte)
http://arxiv.org/pdf/0708.2906.pdf
Es stellt sich dabei heraus, dass diese Gravitationsfelder eine Besonderheit aufweisen, die zu ähnlichen Effekten wie in der Schwarzschildmetrik führt. Betrachten wir zunächst das Gravitationsfeld in x-Richtung sowie die daraus resultierende Bewegungsgleichung in der Newtonschen Mechanik; wir lassen wiederum ein Testteilchen aus der Ruhelage in x-Richtung fallen, geben ihm jedoch zusätzlich eine nicht-verschwindende Geschwindigkeit in der yz-Ebene. Die Bewegungsgleichungen lauten (bei geeigneter Koordinatenwahl)
)
 = v_y t)
 = v_z t)
d.h. die Anziehungskraft in x-Richtung ist unabhängig von der zur x-Richtung senkrechten Geschwindigkeit.
Im Falle des linearen Feldes (als Näherung sehr nahe an der Erdoberfläche) ist a(x) = g, g ist der Ortsfaktor.
Nun betrachten wir das Analogon in der ART; man findet eine modifizierte Bewegungsgleichung
 + b(x,v_\perp))
Der Korrekturterm b bedeutet, dass die „Anziehungskraft“ bzw. die Beschleunigung in x-Richtung abhängig wird von einer dazu senkrechten Geschwindigkeit!! Und dies bedeutet wiederum, dass in einer derartigen Raumzeit Körper nur dann gleich schnell in x-Richtung fallen, wenn sie identische zu x senkrechte Geschwindigkeit haben. Dies kann man für massebehaftete Probekörper und deren Fall aus der Ruhelage immer erreichen. Aber für Photonen funktioniert das nicht, da für diese bei verschwindender Anfangsgeschwindigkeit in x-Richtung für die dazu senkrechte Geschwindigkeit immer (!)

gelten muss.
Zusammenfassend kann man feststellen, dass Photonen mit einer Anfangsgeschwindigkeit senkrecht zum Gravitationsfeld sowie massebehaftete Probekörper in Ruhe nicht gleich schnell in Richtung des Gravitationsfeldes fallen!! Der zu Beginn diskutierte Fall A) stellt eine triviale Ausnahme dar.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 26. Nov 2012 11:37 Titel: Huggy Verfasst am: 26. Nov 2012 11:37 Titel: |
 |
|
Einsteins Arbeit
Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichts
aus dem Jahre 1911 beruht noch auf der SRT. Später hat er die Rechnung im Rahmen der ART wiederholt. Dabei ergab sich für die Lichtablenkung durch die Sonne dasselbe Ergebnis. Nun hat mich interessiert, was sich nach obiger Arbeit für das Photon im Kasten ergäbe. Für die Krümmung 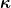 eines Lichtstrahls im Gravitationsfeld mit dem Potential eines Lichtstrahls im Gravitationsfeld mit dem Potential 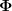 hat Einstein hergeleitet: hat Einstein hergeleitet:

Dabei ist  die Richtungsableitung des Potentials in Richtung der Normalen zur Ausbreitungsrichtung des Lichtstrahls am jeweiligen Ort. Die Winkelablenkung des Lichtstrahls ergibt sich dann durch Integration der Krümmung über die Bahnkurve. die Richtungsableitung des Potentials in Richtung der Normalen zur Ausbreitungsrichtung des Lichtstrahls am jeweiligen Ort. Die Winkelablenkung des Lichtstrahls ergibt sich dann durch Integration der Krümmung über die Bahnkurve.
Betrachtet man ein homogenes Gravitationsfeld der Feldstärke g, das entgegengesetzt der y-Richtung orientiert ist und einen Lichtstrahl, der sich aktuell im Winkel  zur x-Achse bewegt, dann ist zur x-Achse bewegt, dann ist

Für einen in Richtung der x-Achse startenden Lichtstrahl ist zunächst 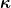 in guter Näherung konstant und der Lichtstrahl bewegt sich näherungsweise auf einem Kreis mit Radius in guter Näherung konstant und der Lichtstrahl bewegt sich näherungsweise auf einem Kreis mit Radius  . Man rechnet leicht aus, dass in der Zeit, in der ein Körper nach klassischer Mechanik um einen Meter nach unten fällt, sich der Lichtstrahl in sehr guter Näherung auch um einen Meter nach unten bewegt hat. . Man rechnet leicht aus, dass in der Zeit, in der ein Körper nach klassischer Mechanik um einen Meter nach unten fällt, sich der Lichtstrahl in sehr guter Näherung auch um einen Meter nach unten bewegt hat.
Für größere Zeiten/Entfernungen ergeben sich aber deutliche Unterschiede zwischen der Bahnkurve des Körpers nach klassischer Mechanik und der Bahnkurve des Lichtstrahls. Es sei y(x) die Bahnkurve. Dann hat man:
^3}}=-\frac {g}{c^2} \cos \alpha= -\frac {g}{c^2}\frac {1}{\sqrt {1+y'^2}})

Die Integration ergibt:
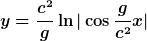
Die Bahnkurve des Körpers nach klassischer Mechanik wäre dagegen

Die Bahnkurve des Lichtstrahls verläuft also steiler als die Bahnkurve des Körpers nach klassischer Mechanik. Man beachte aber, dass sich, außer zu Anfang, auch die Geschwindigkeiten unterscheiden. Interessanterweise kann der Lichtstrahl in horizontaler Richtung die Entfernung

nicht überschreiten.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 26. Nov 2012 15:09 Titel: TomS Verfasst am: 26. Nov 2012 15:09 Titel: |
 |
|
| HaraldK hat Folgendes geschrieben: | Ich habe eine würfelförmige Kiste ... Die Gravitation führt dazu, dass der Weg des Photons ein klein wenig nach unten gebogen ist.
Frage: wie lange dauert es, bis das Photon auf dem Boden der Kiste ankommt? |
Dabei habe ich natürlich angenommen, dass HaraldK den Vergleich zwischen Photon und massebehaftetem Körper immer im Zuge der ART vornimmt.
| Huggy hat Folgendes geschrieben: | Für größere Zeiten/Entfernungen ergeben sich aber deutliche Unterschiede zwischen der Bahnkurve des Körpers nach klassischer Mechanik und der Bahnkurve des Lichtstrahls. Es sei y(x) die Bahnkurve.
...
Die Bahnkurve des Körpers nach klassischer Mechanik wäre dagegen
...
Die Bahnkurve des Lichtstrahls verläuft also steiler als die Bahnkurve des Körpers nach klassischer Mechanik. Man beachte aber, dass sich, außer zu Anfang, auch die Geschwindigkeiten unterscheiden. |
Jetzt vergleichst du Äpfel mit Birnen, denn nun hast du
a) eine nichtrelativistische sowie eine relativistische Bewegung
b) nicht vergleichbare Anfangsbedingungen
c) und du stellst die Frage nach der Bahnkurve, nicht wie oben nach der Zeit
Mein letzter Beitrag ging in die Richtung, dass ich unter ganz speziellen Bedingungen (konstante Beschleunigung formuliert in Rindlerkoordinaten) keine Abweichungen für die „Falldauer“ habe. Aber natürlich habe ich immer (!) Abweichungen für die Bahnkurven, da ich für masselose und massebehaftete Teilchen überhaupt keine identischen Anfangsbedingungen formulieren kann (das ist eigtl. eine ziemlich triviale Aussage)
Ich versuche sozusagen, zumindest vergleichbare (Klassen von) Anfangsbedingungen zu definieren, und stelle fest dass im speziellen Fall der Rindlermetrik alle Bahnkurven mit folgenden Anfangsbedingungen:
- verschwindende Vertikalkomponente der Geschwindigkeit
- beliebige Horizontalkomponente einschließlich lichtartiger Teilchen
gleichzeitig (gemessen in der Koordinatenzeit, nicht der Eigenzeit der jeweils beteiligten Teilchen) am Boden ankommen. Das ist in Rindlerkoordinaten eine nicht-triviale Aussage; sie wird jedoch völlig trivial in Minkowski-Koordinaten, denn da haben wir einfach einen flachen Raum mit einer geraden Bahnkurve sowie einen sich bewegenden Aufzug dessen Boden eine bestimmte Strecke zurücklegen muss, wozu er immer gleich lang braucht, egal was wir da an Teilchen durch den Aufzug durchfliegen lassen.
Aber in anderen Metriken (Gravitationsfeldern) habe ich evtl. eine andere Form der Bewegungsgleichungen, nämlich z.B. eine der Form
 + b(x,v_\perp))
wie z.B. in
http://arxiv.org/abs/0708.2906v1
so dass ich auch bei (möglichst) identischen Anfangsbedingungen nicht nur unterschiedliche Bahnkurven erhalte (trivial) sondern auch unterschiedliche Falldauer.
Ich werde mich mal darum kümmern, wie denn die Bewegungsgleichungen (Geodäten) aussehen müssen, so dass identische Zeiten resultieren..
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 26. Nov 2012 16:43 Titel: Huggy Verfasst am: 26. Nov 2012 16:43 Titel: |
 |
|
@ TomS
Mein Beitrag war nicht als Kontrast und schon gar nicht als Widerspruch zu deinem Beitrag davor gedacht.
Ich habe lediglich aus Interesse versucht, die Einsteinsche Rechnung aus 1911 für ein homogenes Gravitationsfeld durchzuführen. Und er hat dort die Bewegung des Lichtstrahls nach der SRT unter gewissen zusätzlichen Annahmen für die Wirkung der Gravitation mit der Bewegung eines massebehafteten Teilchens verglichen, das sich nach klassischer Mechanik bewegt und mit Anfangsgeschwindigkeit c aus dem Unendlichen kommend an der Sonne vorbeifliegt. Er hat bei diesem Vergleich die doppelte Winkelablenkung des Lichts herausbekommen im Vergleich zu dem Teilchen nach klassischer Mechanik. Weshalb sollte ich nicht denselben Vergleich für ein homogenes Gravitationsfeld versuchen?
Die Anfangsbedingungen habe ich gleich gewählt. Ich lasse auch das klassische Teilchen mit c losfliegen, auch wenn es dass nach der SRT nicht kann. Zur Frage nach der Zeit habe ich für den ein Meter Kasten auch eine Aussage gemacht.
Dass mein Beitrag genau die Frage von HaraldK trifft, habe ich nicht behauptet. Ich hoffe einfach, er findet ihn nicht uninteressant. Insgesamt verstehe ich nicht, weshalb du so harsch reagierst!
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 26. Nov 2012 17:12 Titel: TomS Verfasst am: 26. Nov 2012 17:12 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | Mein Beitrag war nicht als Kontrast und schon gar nicht als Widerspruch zu deinem Beitrag davor gedacht. |
OK
| Huggy hat Folgendes geschrieben: | | Ich habe lediglich aus Interesse versucht, die Einsteinsche Rechnung aus 1911 für ein homogenes Gravitationsfeld durchzuführen. |
OK
| Huggy hat Folgendes geschrieben: | | Dass mein Beitrag genau die Frage von HaraldK trifft, habe ich nicht behauptet. Ich hoffe einfach, er findet ihn nicht uninteressant. |
Dein Beitrag ist nicht uninteressant.
| Huggy hat Folgendes geschrieben: | | Insgesamt verstehe ich nicht, weshalb du so harsch reagierst! |
Harsch? Kam das so rüber? Dann tut's mir leid!
Ich wollte lediglich klarstellen, dass du andere Szenarien vergleichst als das, was urspünglich diskutiert wurde. Keine weitere Kritik oder Tadel oder sonstwas!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
D2

Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
 D2 Verfasst am: 26. Nov 2012 17:40 Titel: D2 Verfasst am: 26. Nov 2012 17:40 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Ich werde mich mal darum kümmern, wie denn die Bewegungsgleichungen (Geodäten) aussehen müssen, so dass identische Zeiten resultieren.. |
Nicht mal SL vermag, dass die Photonen nach Newton fallen.
Ich mus mein Denkfehler korrigieren. Wenn die fallende Gegenstände(manchmal Satellite genannt) Horisontalgeschwindigkeit haben die groß genug sind, dann wierden diese niemals auf dem Boden landen.
http://www.schulphysik.de/java/physlet/applets/newtonberg.html
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
 |
HaraldK
Anmeldungsdatum: 02.10.2012
Beiträge: 54
|
 HaraldK Verfasst am: 26. Nov 2012 18:18 Titel: HaraldK Verfasst am: 26. Nov 2012 18:18 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | HaraldK hat Folgendes geschrieben: | Ich habe eine würfelförmige Kiste ... Die Gravitation führt dazu, dass der Weg des Photons ein klein wenig nach unten gebogen ist.
Frage: wie lange dauert es, bis das Photon auf dem Boden der Kiste ankommt? |
Dabei habe ich natürlich angenommen, dass HaraldK den Vergleich zwischen Photon und massebehaftetem Körper immer im Zuge der ART vornimmt. |
Genau. Stand der Technik, sozusagen.
| TomS hat Folgendes geschrieben: |
Mein letzter Beitrag ging in die Richtung, dass ich unter ganz speziellen Bedingungen (konstante Beschleunigung formuliert in Rindlerkoordinaten) keine Abweichungen für die „Falldauer“ habe.
|
Hoffentlich sehe ich das jetzt nicht zu sehr durch das Brennglas, aber Schwarzschild und Singularitäten im Koordinatensystem lese ich in Deinem letzten Beitrag. Soweit wollte ich das Photon gar nicht fallen lassen. Mich interessiert im Grunde die Wiederholung der einfachen Fallexperimente des Galilei. Ich lasse einen Stein aus 1 Meter Höhe fallen und eben ein Photon.
Klar, ein Photon kann ich nicht einfach fallen lassen, aber ich kann dafür sorgen, dass seine vertikale Geschwindigkeitskomponente zu Anfang gleich 0 ist. Und damit es mir nicht ausbüchst, stecke ich es in die verspiegelte Kiste. Um sicher zu gehen, dass die beiden Fälle noch besser vergleichbar sind, sollte man sicher noch ein konstantes Gravitationsfeld in der Kiste annehmen, da ja sonst, wegen der unterschiedlichen Wege, auf denen dann unterschiedliche Gravitation wirken würde, die Fälle tatsächlich kaum sinnvoll vergleichbar wären.
Habe ich das nun richtig verstanden, dass in dem Fall die Zeitdauer, um den einen Meter vertikal zurück zu legen in beiden Fällen gleich ist, oder nicht. Ihr beiden seid euch ja offenbar noch nicht so richtig einig.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 26. Nov 2012 19:26 Titel: Huggy Verfasst am: 26. Nov 2012 19:26 Titel: |
 |
|
| HaraldK hat Folgendes geschrieben: |
Habe ich das nun richtig verstanden, dass in dem Fall die Zeitdauer, um den einen Meter vertikal zurück zu legen in beiden Fällen gleich ist, oder nicht. Ihr beiden seid euch ja offenbar noch nicht so richtig einig. |
Also noch mal: Mein Beitrag hatte überhaupt keinen Bezug zu dem davorstehenden Beitrag von TomS. Deshalb gibt es da auch keine Einigkeit oder Uneinigkeit.
Wenn ich die Analyse von Einstein aus dem Jahre 1911 richtig auf das homogene Feld angewandt habe, ergäbe sich, dass das Photon die 1 m vertikale Distanz nicht exakt, aber mit nur winziger Abweichung in derselben Zeit zurücklegen würde wie ein fallender Stein. Das war aber damals noch keine Analyse im Rahmen der ART. Wenn man es messen könnte, vermute ich aber, dass die Messung dies bestätigen würde.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 26. Nov 2012 21:59 Titel: TomS Verfasst am: 26. Nov 2012 21:59 Titel: |
 |
|
| HaraldK hat Folgendes geschrieben: | Mich interessiert im Grunde die Wiederholung der einfachen Fallexperimente des Galilei. Ich lasse einen Stein aus 1 Meter Höhe fallen und eben ein Photon.
Klar, ein Photon kann ich nicht einfach fallen lassen, aber ich kann dafür sorgen, dass seine vertikale Geschwindigkeitskomponente zu Anfang gleich 0 ist. Und damit es mir nicht ausbüchst, stecke ich es in die verspiegelte Kiste. Um sicher zu gehen, dass die beiden Fälle noch besser vergleichbar sind, sollte man sicher noch ein konstantes Gravitationsfeld in der Kiste annehmen, da ja sonst, wegen der unterschiedlichen Wege, auf denen dann unterschiedliche Gravitation wirken würde, die Fälle tatsächlich kaum sinnvoll vergleichbar wären.
Habe ich das nun richtig verstanden, dass in dem Fall die Zeitdauer, um den einen Meter vertikal zurück zu legen in beiden Fällen gleich ist, oder nicht. Ihr beiden seid euch ja offenbar noch nicht so richtig einig. |
Ja, im absolut homogenen Gravitationsfeld, bzw. in der von mir verwendeten Rindler-Metrik, die einer im feldfreien Raum konstant beschleunigten Kiste entspricht, fallen Photon sowie ein beliebiger massiver Körper exakt gleich schnell (darüber sind wir uns einig). Aber sie fallen nicht gleich schnell wie in der Newtonschen Mechanik – letztere ist i.A. nicht mehr anwendbar (darüber sind wir uns jetzt auch einig, nur anfangs haben wir aneinander vorbeigeredet).
| HaraldK hat Folgendes geschrieben: | | Hoffentlich sehe ich das jetzt nicht zu sehr durch das Brennglas, aber Schwarzschild und Singularitäten im Koordinatensystem lese ich in Deinem letzten Beitrag. Soweit wollte ich das Photon gar nicht fallen lassen. |
Mir ging es um etwas anderes: du präparierst dein Photon in der Kiste mit „vertikaler Geschwindigkeitskomponente zu Anfang gleich 0“, um sicherzustellen, dass beide Fälle einigermaßen vergleichbar sind. Meine Berechnung in der Rindler-Metrik zeigt, dass alle Bahnkurven für beliebige horizontale Geschwindigkeiten auf dieselbe Falldauer für die vertikale Höhe (von einem Meter) führen. Das schließt auch den Spezialfall deines Photons ein.
Das muss aber nicht in jedem Gravitationsfeld so sein. Es kann sein, dass die vertikale Fallbeschleunigung durchaus von der horizontalen Geschwindigkeitskomponente abhängt (im Gravitationsfeld kann man sich das nicht vorstellen). Im Falle des SLs gibt es einen Photonenorbit, auf dem ein horizontal bewegtes Photon ewig kreist und somit keine vertikale Strecke zurücklegt; die Falldauer für eine feste Strecke wäre in diesem Fall unendlich. Aber jeder massebehaftete Körper müsste zwingend fallen und hätte eine endliche Falldauer.
Damit ist nur gesagt, dass die Eigenschaft von Photon und anderem Testteilchen, in der Kiste gleich schnell zu fallen, eine sehr spezielle Eigenschaft des Gravitationsfeldes der Rindler-Metrik ist (besser gesagt: man kann durch die Transformation ja zeigen, dass überhaupt kein Gravitationsfeld vorliegt, sondern lediglich ein beschleunigtes Bezugssystem für beliebige Testteilchen im feldfreien Raum.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|


















