| Autor |
Nachricht |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Jan 2021 10:53 Titel: index_razor Verfasst am: 03. Jan 2021 10:53 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
@index_razor: ich weiß, was du mit
„Die Tensorableitung hat die Eigenschaft

für alle Funktionen f meinst, aber ich halte das in diesem Zusammenhang für verwirrend.
|
Das ist gelinde gesagt etwas verblüffend. Was bitte ist an "für alle Funktionen f gilt  " schlecht zu verstehen oder verwirrend? Das bedeutet, es gibt keine Funktion, für die etwas anderes gilt. Es muß also auch für Komponenten eines Tensorfeldes gelten, welches Funktionen auf einem Kartengebiet sind. Wenn du das für verwirrend erklärst, untergräbst du lediglich das Verständnis für eine absolute Trivialität. " schlecht zu verstehen oder verwirrend? Das bedeutet, es gibt keine Funktion, für die etwas anderes gilt. Es muß also auch für Komponenten eines Tensorfeldes gelten, welches Funktionen auf einem Kartengebiet sind. Wenn du das für verwirrend erklärst, untergräbst du lediglich das Verständnis für eine absolute Trivialität.
| Zitat: |
Der Physiker lernt dies für „skalare Funktionen“ sowie dass „eine Komponente eines Tensors keine skalare Funktion ist“.
|
Physiker können Differentialgeometrie aus einer Vielzahl von Texten lernen, einige gut, viele nicht so gut. Aus den Fakten, die Physiker über kovariante Ableitungen lernen (bzw. lernen sollten), läßt sich leicht ableiten, daß diese Aussage für alle Funktionen gelten muß. Es gibt keinen mathematisch definierten Unterschied zwischen "skalaren" und "nichtskalaren" Funktionen, der in diesem Zusammenhang eine Rolle spielt. (Und ich behaupte sogar, es gibt auch sonst keinen.)
Das einzige was hier verwirrend ist, ist auf diesem nichtexistenten Unterschied herumzureiten.
| Zitat: |
Damit käme er nie auf die Idee,  in deinem Sinne als eine Funktion aufzufassen. in deinem Sinne als eine Funktion aufzufassen. |
Das sollte er aber. Denn damit kann er nämlich leicht Formeln, wie
^k = \partial_i v^k +\sum_\ell \Gamma^k_{\ell i}v^\ell)
aus einfachen Rechenregeln selbst ableiten. Siehe z.B. hier. Dort wird an der zentralen Stelle verwendet, daß

Also genau die Eigenschaft, die für alle Funktionen gilt, wird hier für die Funktion  benutzt. Diesen einfachen Zusammenhang als "verwirrend" zu bezeichnen und gleichzeitig durch Einführung eines irrelevanten Unterschieds zwischen "skalaren" und "nichtskalaren" Funktionen (der auch noch schlecht definiert ist) zu verkomplizieren, halte ich für kontraproduktiv. benutzt. Diesen einfachen Zusammenhang als "verwirrend" zu bezeichnen und gleichzeitig durch Einführung eines irrelevanten Unterschieds zwischen "skalaren" und "nichtskalaren" Funktionen (der auch noch schlecht definiert ist) zu verkomplizieren, halte ich für kontraproduktiv.
Ist es übrigens nicht gerade der Sinn dieses Forums, den Fragesteller auf Ideen zu bringen, auf die er selbst nicht gekommen ist? Genau das versuche ich jedenfalls.
| Zitat: |
Deinen Beitrag vom 29. halte ich für eine sehr schöne Zusammenfassung, auch wenn die Brücke zur abstrakten Indexnotation offenbar noch nicht wirklich klar wird.
|
Ich habe absichtlich den abstrakten Indexkalkül nur angedeutet, weil ich ihn (besonders didaktisch) für unvorteilhaft halte. Er ist mir ein bißchen zu subtil und ähnelt darin dem Diracformalismus in der QM, den ich auch ungern benutze.
Ich dachte deshalb es wäre besser, alles weitere bei Bedarf auf Nachfrage hin zu klären. Wenn du mir genauer sagst, was noch nicht klar geworden ist, dann versuche ich es besser zu erklären.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Die wichtige Nachricht ist lediglich, daß die Definition
)
überhaupt keine kovariante Ableitung benötigt, also auch erst recht keinen Levi-Civita-Zusammenhang. |
Das kannst du vermöge deines Zugangs so sagen. Wenn dieser Zugang jedoch nicht verwendet wird, dann funktioniert dies grade nicht, dann muss umgekehrt der Laplace-Operator mittels kovarianter Ableitungen definiert werden.
|
Nein, das sage ich nicht vermöge irgendeines Zugangs so. Das ist ein mathematischer Fakt. Nur auf diesen Fakt wollte ich hinweisen. Du hast das m.E. implizit selbst getan, indem du Wikipedia-Artikel verlinkt hast, aus denen genau dasselbe hervorgeht: Der Laplace-Operator auf Formen, also insbesondere auch auf Funktionen, ist definiert als
^2)
Für Funktionen vereinfacht sich das zu  . Darin ist . Darin ist  die natürliche (metrikfreie) Analogie zum Gradienten der Funktion f und die natürliche (metrikfreie) Analogie zum Gradienten der Funktion f und )) die (metrikabhängige) Analogie zur Divergenz eines Vektorfeldes X. Damit ist die (metrikabhängige) Analogie zur Divergenz eines Vektorfeldes X. Damit ist  die natürliche Verallgemeinerung von die natürliche Verallgemeinerung von  . .
Mein Punkt ist nur, daß, egal welchen Zugang du nun zur Differentialgeometrie verwendest, eine Struktur namens "kovariante Ableitung" hierfür nicht benötigt wird.
Eine kovariante Ableitung benötigt man nur, wenn man den Laplace-Operator für beliebige Tensorfelder definieren will, was hier aber offenbar gar nicht beabsichtigt war.
| Zitat: |
Und im Rahmen der theoretischen Physik geschieht dies eben sehr häufig direkt mittels des Levi-Cevita-Zusammenhang. Natürlich kann man für diesen Spezialfall die Äquivalenz zeigen, d.h. man startet eben gerade mit den kovarianter Ableitungen gemäß des Levi-Cevita-Zusammenhangs und leitet die zitierte Formel ab. Es sind Äquivalenzumformungen, die ich in beide Richtungen lesen kann. |
Das weiß ich. Eine dieser Äquivalenzen habe ich ja selbst gezeigt, die andere nur skizziert. Ich verstehe nicht, worauf du hinauswillst. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Jan 2021 17:43 Titel: index_razor Verfasst am: 03. Jan 2021 17:43 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Sobald dies klar ist, wird dies nie als eine Funktion aufgefasst sondern es wird immer als ein Objekt „Tensor zweiter Stufe“ verstanden, mit kovariante Ableitung

Und natürlich kannst du zuletzt auch

einsetzen. Die Notation leistet beides, allerdings um den Preis, dass du wissen musst, wann du etwas tust.
|
Es ist ein bißchen subtiler. Wenn man Komponenten von Tensoren im abstrakten Indexkalkül definieren will, benötigt man zwei Arten von Indizes. Die 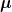 -te Komponente von -te Komponente von  erhält man durch Kontraktion mit dem Basisvektor erhält man durch Kontraktion mit dem Basisvektor  . Dieser hat zwei Indizes. Der Index . Dieser hat zwei Indizes. Der Index 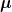 numeriert die Elemente der Basis und läuft von 0 bis 3. Der Index b durchläuft gar nichts und numeriert gar nichts. Er zeigt nur an, daß man numeriert die Elemente der Basis und läuft von 0 bis 3. Der Index b durchläuft gar nichts und numeriert gar nichts. Er zeigt nur an, daß man  mit einem Kovektor kontrahieren kann. Damit gilt der Zusammenhang mit einem Kovektor kontrahieren kann. Damit gilt der Zusammenhang

Das Ergebnis sieht natürlich so aus, als hätte ich einfach a durch 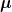 ersetzt. Aber das ist genau das, was ich mit "subtil" meine. Der Kalkül erledigt automatisch viele "Rechenschritte", über die man am Anfang eher in Ruhe nachdenken sollte. Er verwendet fast dieselbe Notation für Tensoren, wie für ihre Komponenten, obwohl dieser Unterschied wichtig ist und deutlich dargestellt werden sollte. Und übrigens, auch im abstrakten Indexkalkül gilt ersetzt. Aber das ist genau das, was ich mit "subtil" meine. Der Kalkül erledigt automatisch viele "Rechenschritte", über die man am Anfang eher in Ruhe nachdenken sollte. Er verwendet fast dieselbe Notation für Tensoren, wie für ihre Komponenten, obwohl dieser Unterschied wichtig ist und deutlich dargestellt werden sollte. Und übrigens, auch im abstrakten Indexkalkül gilt
 = \partial_a g_{\mu\nu}.)
Man kann also nicht sagen, daß irgendeine indizierte Größe nie als Funktion aufgefaßt wird. Es kommt darauf an mit welchen Indizes sie indiziert ist.
Deswegen lasse ich die abstrakten Indizes lieber weg und schreibe
.)
Das finde ich viel klarer. |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 297
|
 Corbi Verfasst am: 03. Jan 2021 22:46 Titel: Corbi Verfasst am: 03. Jan 2021 22:46 Titel: |
 |
|
ok ich denke ich habs jetzt gerafft/ akzeptiert.
Ich glaube ich habe mir schwer getan damit zu verstehen, dass bei der kovarianten Ableitung eines Tensors nicht die Komponenten des Tensors "kovariant abgeleitet" werden. Das ist mit zum einen schwer gefallen, weil es die gebräuchliche Schreibweise irgendwie nahelegt und zum anderen, weil die Notwendigkeit der kovarianten Ableitung ja damit begründet wird, dass sich die partiellen Ableitungen von Tensorkomponenten im allgemeinen nicht wie Tensorkomponenten verhalten. Daher erschien es für mich sinnvoll, dass man eine kovariante Ableitung für die Tensorkomponenten einführt.
Stattdessen ist die kovariante Ableitung aber eine Operation am Tensor selbst, die wieder einen Tensor ergibt. |
|
 |
|
|















