| Autor |
Nachricht |
korbi58
Gast
|
 korbi58 Verfasst am: 09. Aug 2013 10:48 Titel: kürzesteverbindung auf einer kugeloberfläche |
 |
|
mithilfe der eulergleichung kommt man auf
(s1.directupload.net/file/d/3342/5kbjqpk4_png.htm)
allerdings weiß ich nicht wie man weiter auslöst nach phi |
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 09. Aug 2013 13:06 Titel: |
|
|
Was hast Du jetzt davon?
Gruß von Bruce |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 09. Aug 2013 13:58 Titel: |
|
|
Ich würde gefühlsmäßig die Geodäte anders berechnen (weiß aber nicht, ob das funktioniert)
Statt direkt eine beliebige Geodätengleichung in theta und phi zu lösen, würde ich eher eine spezielle Geodäte (z.B. den Äquator) nehmen, und durch Anwendung von Rotationsmatrizen (Eulerwinkeln) alle anderen Geodäten daraus erzeugen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
korbi58
Gast
|
| korbi58 Verfasst am: 09. Aug 2013 14:26 Titel: |
|
|
| Bruce hat Folgendes geschrieben: | gleichung
<br />
) |
sry habs vergessen zuerwählen es handelt sich um phi' also dphi/dtheta
dphi=wurel aus (1) |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 09. Aug 2013 20:10 Titel: |
|
|
Du suchst also
und hast
=\frac{K^2}{\sin^2\theta}\,\frac{1}{\sin^2\theta-K^2}
<br />
)
oder wie 
Verwende
}}\,\frac{df}{d\theta}
<br />
)
Da stellt sich mir gleich die nächste Frage: Kannst Du
selbst berechnen?
Gruß von Bruce |
|
|
korbi58
Gast
|
| korbi58 Verfasst am: 09. Aug 2013 20:27 Titel: |
|
|
sry kann nicht latex
hier ein bild was ich meine
s7.directupload.net/file/d/3342/2erfts6b_jpg.htm |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 09. Aug 2013 21:05 Titel: |
|
|
Ja bin ich denn im Wald hier 
Du willst also
berechnen?
Gruß von Bruce 
Zuletzt bearbeitet von Bruce am 09. Aug 2013 21:20, insgesamt 3-mal bearbeitet |
|
|
korbi58
Gast
|
| korbi58 Verfasst am: 09. Aug 2013 21:16 Titel: |
|
|
|
genau^^ |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 09. Aug 2013 21:19 Titel: |
|
|
Ist das nicht eines von diesen elliptischen Integralen?
Das muß man erst mal auf die passende Standardform transformieren und
dann die numerischen Werte in einer Tabelle nachschlagen oder numerisch berechenen.
Suchst Du etwa jemanden, der dir dabei auf die Sprünge hilft?
So wie ich das sehe, geht da ohne die Werte für  gar nichts.
Gruß von Bruce
Zuletzt bearbeitet von Bruce am 09. Aug 2013 21:55, insgesamt 2-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 09. Aug 2013 21:22 Titel: |
|
|
Das unbestimmte Integral ist laut Mathematika nicht lösbar
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 10. Aug 2013 00:00 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Ich würde gefühlsmäßig die Geodäte anders berechnen (weiß aber nicht, ob das funktioniert)
Statt direkt eine beliebige Geodätengleichung in theta und phi zu lösen, würde ich eher eine spezielle Geodäte (z.B. den Äquator) nehmen, und durch Anwendung von Rotationsmatrizen (Eulerwinkeln) alle anderen Geodäten daraus erzeugen. |
... wobei die kürzeste Verbindung zwischen zwei Punkten auf der Kugeloberfläche immer auf dem Großkreis liegt, also dem Kreis, dessen Mittelpunkt der Kugelmittelpunkt ist (siehe Äquator). |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 10. Aug 2013 08:47 Titel: |
|
|
Für eine Geodäte auf der Kugeloberfläche muß man doch nur sphärische Polarkoordinaten kennen bzw. Längengrad und Breitengrad darin umrechnen können und wissen wie das Skalarprodukt von Vektoren interpretiert wird.
Die von TomS vorgeschlagene Transformation läuft am Ende der Rechnung ja auf das gleiche hinaus, bietet allerdings eine etwas andere Sicht auf das Problem.
Wozu in diesem Fall numerische Integration? Das geht analytisch exakt!
Gruß von Bruce |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 10. Aug 2013 10:02 Titel: |
|
|
| GvC hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Ich würde gefühlsmäßig die Geodäte anders berechnen (weiß aber nicht, ob das funktioniert)
Statt direkt eine beliebige Geodätengleichung in theta und phi zu lösen, würde ich eher eine spezielle Geodäte (z.B. den Äquator) nehmen, und durch Anwendung von Rotationsmatrizen (Eulerwinkeln) alle anderen Geodäten daraus erzeugen. |
... wobei die kürzeste Verbindung zwischen zwei Punkten auf der Kugeloberfläche immer auf dem Großkreis liegt, also dem Kreis, dessen Mittelpunkt der Kugelmittelpunkt ist (siehe Äquator). |
Ja, natürlich, deswegen habe ich ja gesagt " eine spezielle Geodäte (z.B. den Äquator)". Der Vorteil ist, dass ich den Äquator, also die Geodäte, und die Rotationsmatrizen explizit hinschreiben kann. Damit bekomme ich also sicher eine Darstellung aller Geodäten.
Das Problem ist dann die Konstruktion der Drehung, wenn ich für zwei bestimmte Punkte die Geodäte suche.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 10. Aug 2013 10:06 Titel: |
|
|
Dazu fällt mir nochmal etwas ein. Das Problem bei der Konstruktion der Rotationsmatrizen ist ja letztlich die Konstruktion der Drehachse.
Ich denke, da gibt es eine Alternative. Nehmen wir an, wir haben zwei Einheitsvektoren vom Kugelmittelpunkt zu zwei beliebigen Punkten i=1,2 auf der Kugeloberfläche. Die Geodäte zwischen den Punkten verläuft dann in der Ebene, die durch die beiden Vektoren aufgespannt wird. Genauer: die Geodäte = der gesamte Großkreis entspricht dem Schnitt der Kugeloberfläche mit der Ebene. Die Rotationsachse steht senkrecht auf den beiden Vektoren, ist also durch das Kreuzprodukt gegeben. Man findet die Geodäte also dadurch, dass man den ersten Vektor um die so definierte Drehachse rotiert. Der maximale Rotationswinkel wird dann durch das Skalarprodukt der beiden Vektoren definiert.
D.h. die beiden Punkte sind gegeben durch
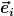
die Drehachse durch
und der maximale Drehwinkel um die Drehachse durch
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 11. Aug 2013 10:55, insgesamt 2-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 10. Aug 2013 10:42 Titel: |
|
|
Noch etwas, keine neue Methode, sondern ggf. eine Vereinfachung der Algebra.
Anstatt mit 3*3 Matrizen der SO(3) zu rechnen, ist die Nutzung der komplexen 2*2 Matrizen der SU(2) evtl. einfacher. Das funktioniert aufgrund der lokalen Isomorphie der beiden Drehgruppen. Der wesentliche Vorteil der SU(2) ggü. der SO(3) ist, dass bei expliziter Kenntnis der Rotationsachse (n, s.o.) die Rotation direkt hingeschrieben werden kann, während das bei der SO(3) und Eulerwinkeln nicht direkt und nicht eindeutig funktioniert.
Ich denke, dass die SU(2) - bzw. Einheitsquaternionen, was letztlich das selbe ist - in der Computergraphik für Drehungen verwendet werden. Es sollte da also fertige Formeln geben.
Zur Idee siehe: http://www.uni-koblenz.de/~cg/veranst/ws0001/sem/Lust_quaternion.pdf sowie einfach googeln nach 'computergrafik quaternion'
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 10. Aug 2013 14:40 Titel: |
|
|
@TomS
Ich vermute dir ist klar, daß die Abbildung durch Drehung auf den Äquator
zur Berechnung der Länge einer Geodäte auf der Kugeloberfläche nicht
erforderlich ist. Die Kenntnis von  genügt.
Daraus berechnet man  im Bogenmaß und ist fast fertig.
Wenn geographische Koordinaten wie z.B. für
Frankfurt (50.050777° Breite, 8.564129° Länge)
und
Honolulu (21.306944 Breite, -157.858337 Länge)
(Quelle: www.luftlinie.org , hier sieht man die Geodäte in Mercatorprojektion)
gegeben sind, dann ist damit auch schon die Lage dieser Punkte bezüglich
eines speziell definierten Koordinatensystems festgelegt, d.h. man kann
 und  bezüglich dieses Koordinatensystems angeben und daraus das koordinatenunabhängige Skalarprodukt berechnen.
Aber deinen Hinweis auf die lokale Isomorphie von SU2 und SO3 merke ich mir
schon mal vor. Wir wollen schließlich nicht nur irgendwie richtig rechnen sondern
gerne auch schlau und elegant. Mal schauen, wann sich eine Verwendungsmöglichkeit
dafür ergibt.
Für die Berechnung von Computergrafiken ist natürlich die Vermeidung rationaler
Multiplikationen (sehr teuere arithmetische Operation) zur Beschleunigung der Rechnung
sehr wichtig. Der Quaternionenansatz bietet hier eine Möglichkeit.
Das wusste ich noch nicht (wie so vieles), danke für den Hinweis!
Gruß von Bruce
Zuletzt bearbeitet von Bruce am 10. Aug 2013 21:22, insgesamt einmal bearbeitet |
|
|
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
| Huggy Verfasst am: 10. Aug 2013 15:23 Titel: |
|
|
Es wäre erst mal zu klären, was die Aufgabenstellung ist.
Soll die Länge einer Geodäte auf der Kugel zwischen zwei gegebenen Punkten berechnet werden, wobei als bekannt vorausgesetzt wird, dass die Geodäte ein Großkreis ist? Das wäre in der Tat eine simple Aufgabe.
Oder soll mit Hilfe der Euler-Lagrange-Gleichungen bewiesen werden, dass die Geodäten auf der Kugel gerade die Großkreise sind? Das wäre eine ganz andere Aufgabe. Vom Fragesteller wurde zu Beginn des Threads die Euler-Gleichung erwähnt. |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 10. Aug 2013 15:39 Titel: |
|
|
@Huggy
Der Fragesteller ist sehr wortkarg, deswegen haben wir uns erlaubt ein wenig
zu interpretieren. Vielleicht sind wir dabei vom Weg abgekommen. Aber
wenn jemand nicht so recht weiß, ober er Integral oder Ableitung sucht, dann
sind Mißverständisse vorprogrammiert. Es ist doch trotzdem ein sehr sachlicher
und interessanter Gedankenaustausch dabei herausgekommen.
Was will man mehr 
Gruß von Bruce |
|
|
korbi58
Gast
|
| korbi58 Verfasst am: 10. Aug 2013 21:02 Titel: |
|
|
danke für die ausführliche antworten, die ich (noch)nicht verstehe 
@Bruce in welchen semester bist du? bisher habe ich (4tes semster noch nichts von elliptische integrale gehört |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 10. Aug 2013 21:18 Titel: |
|
|
Wenn ich heute noch Student wäre, dann wäre die Anzahl meiner Semester
etwa fünfzig. Nein nein, die Studentenzeit ist für mich schon lange vorbei!
Die elliptischen Integrale werden von den Mathematikern im Rahmen der
algebraischen Geometrie untersucht. Davon habe ich aber gar keine Ahnung.
Mein schlaues Buch (blauer Bronstein) flüstert mir diese Dinge ein.
Bei der exakten Berechnung der Periodendauer des mathematischen Pendels
stößt man als Physiker auf ein elliptisches Integral oder bei der Berechnung
von Ellipsenbögen (Keplerproblem).
Gruß von Bruce |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 10. Aug 2013 22:55 Titel: |
|
|
@Bruce: ja, das mit der Länge ist mir natürlich klar; es ging mit ja um die Herleitung einer exakten Darstellung einer beliebigen Geodäte (ohne Lösung einer DGL)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 10:55 Titel: |
|
|
Nochmal zurück zur Konstruktion der Geodäten mittels Quaternionen.
Die beiden durch die Geodäte zu verbindenden Punkte i=1,2 sind gegeben durch
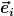
die Drehachse durch
und der maximale Drehwinkel um die Drehachse durch
Wir rotieren nun den Punkt i=1 in den Punkt i=2. Dazu konstruieren wir (in Polardarstellung) die Quaternionen
 = [\cos\phi, \vec{n}\sin\phi])
entsprechend dem Punkt i=1 sowie einer Rotation um die oben definierten Achse und um eine beliebigen Winkel.
Die Geodäte zwischen i=1 und i=2 ist dann definiert durch die Quaternionfunktion
 = r(\phi) \cdot q_1 \cdot r^\ast(\phi),\;\;\phi \in[0,\Phi/2])
mit
 = q_1)
 = q_2)
Aus der Quaternionenfunktion kann man den rotierten Einheitsvektor ablesen
 = [0, \vec{e}(\phi)])
Der Rest ist etwas längliche, aber elementare Matrizenmultiplikation.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
korbi58
Gast
|
| korbi58 Verfasst am: 11. Aug 2013 11:21 Titel: |
|
|
| Huggy hat Folgendes geschrieben: | Es wäre erst mal zu klären, was die Aufgabenstellung ist.
|
das primäre ziel dieser aufgabe wars, sich mit der variationsrechnung vertraut zumachen
d.h finde die kürzeste verbindung zwischen zwei punkten auf der kugeloberfläche |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 11:23 Titel: |
|
|
| korbi58 hat Folgendes geschrieben: | | Huggy hat Folgendes geschrieben: | Es wäre erst mal zu klären, was die Aufgabenstellung ist.
|
das primäre ziel dieser aufgabe wars, sich mit der variationsrechnung vertraut zumachen
d.h finde die kürzeste verbindung zwischen zwei punkten auf der kugeloberfläche |
Dann hilft dir meine Betrachtung eher wenig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
korbi58
Gast
|
| korbi58 Verfasst am: 11. Aug 2013 11:51 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Dann hilft dir meine Betrachtung eher wenig. |
zwar nicht direkt, aber ist es schön zusehen wie man so eine aufgabe aus verschiedener perspektiven lösen kann und vor allem das es leichtere wege gibt
zudem sehe ich endlich eine anwendung der einheitsquaternionen
P.S ich tun mir zwar schwer alles zu verstehen, was alles hier geschrieben würde, aber da muss ich wohl durch |
|
|
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
| Bruce Verfasst am: 11. Aug 2013 14:17 Titel: |
|
|
@korbi58
| Zitat: |
das primäre ziel dieser aufgabe wars, sich mit der variationsrechnung vertraut zumachen
d.h finde die kürzeste verbindung zwischen zwei punkten auf der kugeloberfläche
|
Schön das Du das nach drei Seiten mal nebenei so einstreust 
Warum nicht gleich zu Beginn? Aber egal, war trotzdem interessant.
Sonst hätten wir sicher nichts von den Quaternionen erfahren 
Gruß von Bruce
Zuletzt bearbeitet von Bruce am 11. Aug 2013 17:18, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 14:51 Titel: |
|
|
| korbi58 hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Dann hilft dir meine Betrachtung eher wenig. |
zwar nicht direkt, aber ist es schön zusehen wie man so eine aufgabe aus verschiedener perspektiven lösen kann ... |
Man kann natürlich eine Verbindung wie folgt herstellen:
1) Man löst die Geodätengleichung speziell für den Äquator (das ist letztlich ein Einzeiler).
2) Dann argumentiert man mittels Rotationssymmetrie, dass eine beliebig rotierte Geodäte wieder eine Geodäte ist (ohne Rechnung)
3) Dann argumentiert man (wieder mittels Rotationssymmetrie), dass man jede Geodäte auf den Äquator rotieren kann (zuerst legt man den Äquator durch den Startpunkt, dann rotiert man um eine Drehachse durch den Startpunkt den Endpunkt ebenfalls auf den Äquator) (wieder ohne Rechnung)
4) Aufgrund der Invertierbarkeit jeder Rotation (Gruppeneigenschaft) kann man also auch den Äquator auf jede beliebige Geodäte rotieren (wieder ohne Rechnung)
5) Zuletzt zeigt man, dass die in (1) konstruierte Geodäte als Lösung der Geodätengleichung auch durch die o.g. quaternionische Rotation erzeugt werden kann (das sollten wiederum nur wenige Zeilen sein).
6) Damit hat man gezeigt, dass jede beliebige Geodäte durch die o.g. Rotation erzeugt werden kann (hier steckt der eigentliche Aufwand in den Beweisen der Eigenschaften der quaternionischen Rotation bzw. der lokalen Isomorphie zwischen SU(2) und SO(3) - siehe z.B. das oben verlinkte PDF)
Außer in (1) und in (5) sowie in den Formeln zur quaternionischen Rotation (6) muss man dazu nichts rechnen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
| Huggy Verfasst am: 11. Aug 2013 15:24 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | korbi58 hat Folgendes geschrieben: | | Huggy hat Folgendes geschrieben: | Es wäre erst mal zu klären, was die Aufgabenstellung ist.
|
das primäre ziel dieser aufgabe wars, sich mit der variationsrechnung vertraut zumachen
d.h finde die kürzeste verbindung zwischen zwei punkten auf der kugeloberfläche |
Dann hilft dir meine Betrachtung eher wenig. |
Die Betrachtung hat schon ihren Nutzwert. Allerdings braucht man keine explizite Darstellung der Rotationen. Die beiden Punkte auf der Kugel, deren kürzeste Verbindung gesucht ist, seien ) und ) . Durch Rotationen kann man sie auf die Positionen ) und ) bringen. Es genügt zu wissen, das das geht. Auch  braucht nicht explizit bestimmt zu werden, obwohl das mit den Ausführungen von TomS und Bruce ganz einfach geht.
Kurven zwischen  und  seien durch eine Parameterdarstellung
 \text { mit } \phi(0)=\phi (\theta_3)=0)
mit 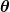 als Parameter beschrieben. Die Länge der Kurve ist
^2+r^2 (\frac {d \theta}{d \theta})^2+r^2\sin^2 \theta (\frac {d \phi}{d \theta})^2} d \theta=\int\limits_0^{\theta_3} \sqrt {r^2 +r^2\sin^2 \theta (\frac {d \phi}{d \theta})^2}d \theta=r\int\limits_0^{\theta_3} \sqrt {1+\sin^2 \theta \phi'^2}d \theta)
mit
Mit
lautet die Euler-Lagrange-Gleichung zur Bestimmung der kürzesten Kurve:
Es ist  und
Daraus folgt
mit einer konstanten K. Diese Gleichung muss für alle 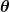 auf der Kurve gelten, also auch für  . Das ergibt K = 0. Und das ergibt dann
für alle 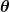auf der Kurve. das geht nur mit
Die kürzeste Verbindung ist also der Meridian. Zurückrotiert ist das der Großkreis durch die ursprünglichen Punkte.
@Tom S
Den Einzeiler für Äquator = Geodäte bitte vorrechen. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 16:23 Titel: |
|
|
| Huggy hat Folgendes geschrieben: | @Tom S
Den Einzeiler für Äquator = Geodäte bitte vorrechen. |
Wie so oft hängt das davon ab, wo man mit dem Zählen der Zeile beginnt, und ob man das DIN A3 Blatt quer nimmt (so wie ein Bekannter in der QFT II Vorlesung) oder nicht.
Wir starten mit der Definition der Kurvenlänge und der Geodäte als Extremfällen Kurve, d.h. verschwindender Variation
Wir führen das äquivalente Energiefunktional ein, das letztlich auf die Lagrangefunktion eines freien Teilchens auf der Kugeloberfläche führt
Die Euler-Lagrange-Gleichungen lauten
Aus den letzten beiden Gleichungen liest man sofort ab, dass der Äquator durch
 = \omega t,\;\;\dot{\phi}=\omega=\text{const.},\;\;\theta(t)=\pi/2=\text{const.})
definiert ist.
Ich würde mal sagen, dass mit dem Wissen, dass ein freies Teilchen jeweils einer Geodäte auf der unterlagerten Mannigfaltigkeit folgt, und dass die Bewegungsgleichungen des freien Teilchens auf der Kugeloberfläche bekannt sind, die Lösung der Bewegungsgleichung als Einzeiler durchgeht ;-) Ansonsten entsprechend mehr Zeilen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 11. Aug 2013 18:20, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 17:06 Titel: |
|
|
Für den Zusammenhang zwischen Äquator und quanternionischer Rotation startet man mit
Für den Äquator gilt
 = (\cos 2\phi, -\sin 2\phi, 0))
Für die Quaternionen bzw. die SU(2) gilt
 = [\cos\phi, \vec{e}_z\sin\phi] = \cos\phi + i\sigma^z\sin\phi)
Für die Rotation setzt man ein
 = r(\phi) \cdot q_1 \cdot r^\ast(\phi) = [\cos\phi + i\sigma^z\sin\phi]\,i\sigma^x\,[\cos\phi - i\sigma^z\sin\phi])
Ausmultiplizieren unter Verwendung der Rechenregeln der Paulimatrizen liefert
 = i\sigma^x\cos 2\phi - i\sigma^y \sin 2\phi)
Dies entspricht aber direkt dem oben angegebenen Vektor für den Äquator.
Man beachte, dass eine Rotation ausgedrückt durch Quaternionen immer mit dem halben Winkel anzusetzen ist (oder alternativ, dass eine quaternionische Rotation immer einer normalen Rotation um den doppelten Winkel entspricht)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 11. Aug 2013 18:22, insgesamt 4-mal bearbeitet |
|
|
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
| Huggy Verfasst am: 11. Aug 2013 17:10 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Ich würde mal sagen, dass mit dem Wissen, dass ein freies Teilchen jeweils einer Geodäte auf der unterlagerten Mannigfaltigkeit folgt, und dass die Bewegungsgleichungen des freien Teilchens auf der Kugeloberfläche bekannt sind, die Lösung der Bewegungsgleichung als Einzeiler durchgeht ;-) Ansonsten entsprechend mehr Zeilen. |
Ich vermute, dass hiermit und dem durchaus nicht trivialen Übergang von  zu  Dinge benutzt werden, die der Fragesteller nicht kennt und daher nicht benutzen darf. Aber dazu kann er sich ja mal äußern.
Ich habe ausschließlich mit gearbeitet, wobei das S bei mir L heißt. Damit darf er sicher arbeiten. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 18:03 Titel: |
|
|
Na ja, ist das nicht einfach die Bestimmung der Extrema von g(x) bzw. f(g(x)) unter Benutzung der Kettenregel, d.h.
Die Extrema von f und g in x sind also identisch, sofern nur
d.h. solange f streng monoton in g ist.
Ich gebe zu, das muss man sich erst mal klar machen. Aber für Geodäten auf beliebigen Mannigfaltigkeiten (u.a. auch in der ART) wird das immer wieder benutzt, um die Rechnungen kompakter zu halten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
| Huggy Verfasst am: 11. Aug 2013 18:50 Titel: |
|
|
So einfach ist das nicht. Es wird ja nicht einfach die Bogenlänge (= Integral über das Bogenlängenelement) quadriert. Das Quadrat der Bogenlänge hat natürlich sein Extremum an derselben Stelle wie die Bogenlänge, weil es eine streng monotone Funktion der Bogenlänge ist. Beim Energiefunktional wird aber erst das Bogenlängenelement quadriert und dann darüber integriert und das ist etwas ganz anderes. In diesem Papier
http://www.uni-math.gwdg.de/schick/teach/Kurven_und_Flaechen/Geodaeten.pdf
braucht es z. B. schon einige Seiten, um zu zeigen, dass beides trotzdem äquivalent ist. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 19:06 Titel: |
|
|
| Huggy hat Folgendes geschrieben: | So einfach ist das nicht. Es wird ja nicht einfach die Bogenlänge (= Integral über das Bogenlängenelement) quadriert. Das Quadrat der Bogenlänge hat natürlich sein Extremum an derselben Stelle wie die Bogenlänge, weil es eine streng monotone Funktion der Bogenlänge ist. Beim Energiefunktional wird aber erst das Bogenlängenelement quadriert und dann darüber integriert und das ist etwas ganz anderes. In diesem Papier
http://www.uni-math.gwdg.de/schick/teach/Kurven_und_Flaechen/Geodaeten.pdf
braucht es z. B. schon einige Seiten, um zu zeigen, dass beides trotzdem äquivalent ist. |
Das sehe ich nicht so. Direkt unter den Definitionen 3.1 und 3.2 für Bogenlänge L und Energiefunktional E steht das Lemma 3.1 mit der Folgerung dass eine Verbindungskurve minimale Energie genau dann hat, wenn sie minimale Länge hat und proportional zur Bogenlänge parametrisiert ist.
Außerdem liefert die funktionale Ableitung der beiden Integrale dieselben Geodätengleichungen - bis auf einen Faktor entsprechend der Kettenregel.
}{\partial \dot{x}^i} \sim f^\prime (\sqrt{g_{mn}\,\dot{x}^m\,\dot{x}^n}) \cdot \frac{\partial \sqrt{g_{mn}\,\dot{x}^m\,\dot{x}^n}}{\partial \dot{x}^i} )
Und in unserem Fall ist f(...) einfach (...)^2.
Mehr braucht es nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 12. Aug 2013 00:37, insgesamt einmal bearbeitet |
|
|
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
| Huggy Verfasst am: 11. Aug 2013 19:36 Titel: |
|
|
Natürlich steht das da. Dieser Sachverhalt sollte ja gerade hergeleitet werden. Aber er wird nicht aus  hergeleitet, weil das nicht gilt. Entscheidend für den Nachweis, dass die Variation von L und E beides zu den Geodäten führt, ist die Parametrisierung der Kurve c nach den Bogenlänge in E. Bei L ist das egal, weil L unabhängig von der Parametriserung ist. Die Parametrisierung der Kurve c nach der Bogenlänge in E bedeutet physikalisch bis auf eventuell einen Faktor gerade, dass man die Kurve mit konstanter Geschwindigkeit durchläuft.
Der Sachverhalt ist also nicht einfach eine Folge der Kettenregel. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 11. Aug 2013 20:01 Titel: |
|
|
| Huggy hat Folgendes geschrieben: | | ... aber er wird nicht aus hergeleitet, weil das nicht gilt. |
Das habe ich auch nicht behauptet.
Der Zusammenhang gilt nicht für die Integrale sondern für die Integranden. Und da gilt er allgemein für beliebige Funktionen f (unter der Voraussetzung der Parametrisierung nach der Bogenlänge)
D.h.
sowie beliebige andere Integranden der Form
)
führen auf die selben Extreme = Geodäten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 12. Aug 2013 07:37 Titel: |
|
|
Mir fällt gerade auf, dass ich da evtl. einen schweren Denkfehler begehe ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
| Huggy Verfasst am: 12. Aug 2013 07:49 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Der Zusammenhang gilt nicht für die Integrale sondern für die Integranden. Und da gilt er allgemein für beliebige Funktionen f (unter der Voraussetzung der Parametrisierung nach der Bogenlänge) |
Zunächst mal, wo ergäbe sich denn aus deiner Argumentation, dass beim quadrierten Integranden eine Parametrisierung nach der Bogenlänge vorliegen muss? Das
gilt für jede Parametrisierung. Die Funktionalableitung führt aber eh nicht zu Ableitungen des Integranden mit nur ersten Ableitungen. In den Euler-Lagrange-Gleichungen stehen auch zweite Ableitungen. Und nach deren Bildung lässt sich f' nicht mehr einfach ausklammern, weil es trotz Kettenregel nicht in jedem Term auftaucht. |
|
|
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
| Huggy Verfasst am: 12. Aug 2013 07:50 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Mir fällt gerade auf, dass ich da evtl. einen schweren Denkfehler begehe ... |
Diesen Beitrag hatte ich noch nicht gesehen. Da hätte ich mir die vorige Antwort sparen können. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18198
|
| TomS Verfasst am: 12. Aug 2013 08:07 Titel: |
|
|
| Huggy hat Folgendes geschrieben: | | Zunächst mal, wo ergäbe sich denn aus deiner Argumentation, dass beim quadrierten Integranden eine Parametrisierung nach der Bogenlänge vorliegen muss? |
Das kann man per Konstruktion erreichen.
| Huggy hat Folgendes geschrieben: | | In den Euler-Lagrange-Gleichungen stehen auch zweite Ableitungen. Und nach deren Bildung lässt sich f' nicht mehr einfach ausklammern. |
Das ist das Problem.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
Registrieren
Login
FAQ
Suchen
