| Autor |
Nachricht |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 01. Nov 2009 10:43 Titel: Mathematische Zeichen bei Kinematik Physinetz Verfasst am: 01. Nov 2009 10:43 Titel: Mathematische Zeichen bei Kinematik |
 |
|
Hallo, wollte nur mal ein paar Zeichen klären was das heißt:
Es gilt für die Momentanbeschleunigung:
Erster Teil
= \lim_{\delta t \to 0} \frac{\delta v_x}{\delta t}=\frac{dv_x}{dt} = \frac{d}{dt} * v_x(t) )
Also dass die Momentanbeschleunigung die erste Ableitung der Geschwindigkeitsfunktion ist, ist mir klar, nur die Zeichen hierfür nicht.
Warum habe ich hier noch ein Index mit x ? )
= \lim_{\delta t \to 0} \frac{\delta v_x}{\delta t})
Hier lasse ich ja beim Differenzenquotient die Zeitänderung gegen Null laufen, so habe ich ja dann den Differentialquotient....

Für was steht das "d" jeweils plötzlich? Kann man es als "Ableitung" lesen? Also Ableitung von 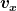 lesen und unten eben das "dt" als Ableitung der Zeit ? lesen und unten eben das "dt" als Ableitung der Zeit ?
Zweiter Teil
= \frac{d²(x(t))}{dt²} = x''(t))
Hinweis: Also hinten bedeutet das 2. Ableitung von x(t)
a)Ich habe hier ja ein d² und unten ein t² , sagt mir dass dann praktisch aus, dass die Beschleunigung eine Funktion mit einem Grad von 2 weniger ist? Also der Grad von x(t) um 2 größer ist?
b)Wie sieht es bei einer ungleichmäßig beschleunigten Bewegung aus, da habe ich ja dann ein Polynom erster Ordnung, folglich müsste ich als x(t) ein Polynom 3. Ordnung erhalten?
Vielen Dank für eure Hilfe
 |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 01. Nov 2009 11:29 Titel: Re: Mathematische Zeichen bei Kinematik MI Verfasst am: 01. Nov 2009 11:29 Titel: Re: Mathematische Zeichen bei Kinematik |
 |
|
| Physinetz hat Folgendes geschrieben: |
Erster Teil
= \lim_{\delta t \to 0} \frac{\delta v_x}{\delta t}=\frac{dv_x}{dt} = \frac{d}{dt} * v_x(t) )
|
Gehe ich Recht in der Annahme, dass dort eigentlich stehen sollte:
= \lim_{\Delta t \to 0} \frac{\Delta v_x}{\Delta t}=\frac{dv_x}{dt} = \frac{d}{dt} * v_x(t) )
Dann bezeichnet 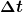 also ein endlich großes Zeitintervall, was gegen Null läuft. Zu den restlichen Symbolen weiter unten. also ein endlich großes Zeitintervall, was gegen Null läuft. Zu den restlichen Symbolen weiter unten.
| Zitat: |
Warum habe ich hier noch ein Index mit x ? )
= \lim_{\delta t \to 0} \frac{\delta v_x}{\delta t})
|
Vermutlich ist gemeint, dass du damit die Beschleunigung in x-Richtung berechnest. Das wird häufig durch kleine Indizes angezeigt. Wenn du dreidimensional ableitest, dann ist ja nicht sofort klar, in welcher Richtung du die Steigung berechnest.
Da aber, wenn die Ableitung existiert, sie durch die partiellen Ableitungen nach den Koordinatenrichtungen ausgedrückt werden kann, berechnet man meist letztere.
| Zitat: |

|
Nun zu diesem Symbol - bzw. dem ganzen Rest:
Die Schreibweise

ist die sogenannte "Leibniz-Schreibweise" der Ableitung und wird in der Physik bevorzugt angewandt. Du hast ja schon die Ähnlichkeit zum Differenzenquotienten erkannt. Wenn du aber jetzt das Zeitintervall beliebig klein werden lässt - also infinitesimal, dann wird ja auch die entsprechende Änderung in v infinitesimal. Und das ist es, was dort oben steht: Du teilst eine infinitesimale Änderung in der Geschwindigkeit  durch eine infinitesimale Änderung in der Zeit durch eine infinitesimale Änderung in der Zeit 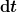 . Du tust also so, als ob du die Tangentensteigung auch durch ein Dreieck berechnest, dessen Punkte einen infinitesimalen (=unendlich kleinen) Abstand haben. Das ist ja im Grunde das Prinzip der Ableitung. . Du tust also so, als ob du die Tangentensteigung auch durch ein Dreieck berechnest, dessen Punkte einen infinitesimalen (=unendlich kleinen) Abstand haben. Das ist ja im Grunde das Prinzip der Ableitung.
Aber jetzt VORSICHT:
Natürlich ist diese Schreibweise eigentlich nicht ganz so einfach. Man kann sie sich als Bruch vorstellen - aber eigentlich ist es kein Bruch. Du darfst also nicht so einfach kürzen oder so etwas. Es handelt sich immer noch um Größen, wo eventuell 0/0 steht. Eigentlich hast du hier einen OPERATOR. Es gilt:
=\frac{\mathrm{d}}{\mathrm{d}x}f(x)=\frac{\mathrm{d}f(x)}{\mathrm{d}x})
Das  solltest du also mathematisch so ähnlich wie ein Plus oder ein Mal betrachten, nur dass es dir sagt: Differenziere doch bitte. solltest du also mathematisch so ähnlich wie ein Plus oder ein Mal betrachten, nur dass es dir sagt: Differenziere doch bitte.
Bevor du fragst: "Und warum sagt man nicht einfach f'(x)?":
Betrachte folgendes Beispiel:
=?)
Wonach wird abgeleitet? Die Apostrophschreibweise sagt dir da nichts.
)
sagt dir, dass du die von mehreren Variablen abhängige Funktion nach x ableiten sollst. Falls noch weitere Variablen von x abhängig sind - Kettenregel.
Jetzt möchtest du die zweite Ableitung bilden. Man schreibt:
1. Ableitung:
=\frac{\mathrm{d}v_x}{\mathrm{d}t}\equiv \dot{v})
2. Ableitung:
=\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{d}v_x}{\mathrm{d}t}\right)=\frac{\mathrm{d}^2v_x}{\mathrm{d}t^2}\equiv \ddot{v})
Eine entsprechende Erweiterung auf die n-te Ableitung liegt wohl auf der Hand  . Das ganze hat also nichts mit Polynomen zu tun - es zeigt dir einfach nur an, wie oft du nach der entsprechenden Variablen ableiten musst. Der Hintergrund ist der: . Das ganze hat also nichts mit Polynomen zu tun - es zeigt dir einfach nur an, wie oft du nach der entsprechenden Variablen ableiten musst. Der Hintergrund ist der:
Meist betrachtest du - wie oben angedeutet - partielle Ableitungen, also Ableitungen von Funktionen einer Variablen nach mehreren Variablen. Dabei darfst du, wenn die Ableitungen gewisse Stetigkeitsvoraussetzungen erfüllen, auch Ableitungen vertauschen. Nun kommt es vor, dass du hohe Ableitungen bilden musst - da kommt dir diese Schreibweise entgegen:
Der Term:
}{\partial z}\right)\right)\right)=\frac{\partial^4 f(x,y,z)}{\partial x^2\partial y \partial z})
(das  steht für partielle Ableitung, also wie ein steht für partielle Ableitung, also wie ein  , nur eben nach einer bestimmten Variablen) , nur eben nach einer bestimmten Variablen)
ist nun wie folgt zu interpretieren:
Insgesamt musst du die Funktion f viermal differenzieren. Davon zweimal nach x, einmal nach y und einmal nach z.
Ich denke du siehst ein, dass diese Schreibweise der Schulschreibweise überlegen ist  . .
Gruß
MI |
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 01. Nov 2009 12:50 Titel: Physinetz Verfasst am: 01. Nov 2009 12:50 Titel: |
 |
|
Wow, klasse Text ! Danke für deine Mühe !!!
Jetzt versuche ich das mal alles zu checken, das mit dem "nicht kürzen" bereitet mir wahrscheinlich noch Schwierigkeiten... |
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 01. Nov 2009 13:05 Titel: Physinetz Verfasst am: 01. Nov 2009 13:05 Titel: |
 |
|
dx , dy bereitet mir iwie Schwierigkeiten:
Bei z.B.

bedeutet doch , dass ich die Stammfunktion von 2x, mit der Differenz von der oberen Grenze und der unteren Grenze multiplizieren muss
also bei z.B.
=\int_{2}^{3}~2x~dx = \left[x²\right]_{2}^{3} = 9 - 4)
Das heißt das dx muss ich als "Differenz der x-Werte" lesen?
Puh das geht mir nicht in meinen kopf...^^ |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 01. Nov 2009 15:50 Titel: MI Verfasst am: 01. Nov 2009 15:50 Titel: |
 |
|
| Physinetz hat Folgendes geschrieben: | dx , dy bereitet mir iwie Schwierigkeiten:
Bei z.B.

bedeutet doch , dass ich die Stammfunktion von 2x, mit der Differenz von der oberen Grenze und der unteren Grenze multiplizieren muss
|
Nein, das bedeutet es NICHT. Dass du das darfst, sagt dir nur der Hauptsatz der Integral- und Differentialrechnung. Das Integral selbst ist unabhängig davon definiert.
Aber die Frage ist: Wie ist es denn definiert? Das Riemann Integral erhälst du ja so:
 \,\mathrm{d}x=\lim\limits_{n\to \infty} \sum\limits_{k=1}^{n}\frac{b-a}{n}\cdot f(a+k\cdot \frac{b-a}{n}))
Was also im Grunde passiert ist, dass du eine Summe bildest. Und genau das sagt dir das Integral:
Du bildest eine Summe
 ist ein altes S für Summe ist ein altes S für Summe
über infinitesimale Summanden:
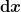
Das kannst du dir im Übrigen schon einmal merken: Immer wenn du in der Physik (z.B. beim Trägheitsmoment) von einer diskreten Verteilung zu einer kontinuierlichen gehst, wird die Summe zu einem Integral.
EDIT: Also insgesamt ist das 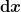 einfach nur als infinitesimales einfach nur als infinitesimales 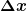 zu verstehen. zu verstehen.
Gruß
MI |
|
 |
|
|

















 . Das ganze hat also nichts mit Polynomen zu tun - es zeigt dir einfach nur an, wie oft du nach der entsprechenden Variablen ableiten musst. Der Hintergrund ist der:
. Das ganze hat also nichts mit Polynomen zu tun - es zeigt dir einfach nur an, wie oft du nach der entsprechenden Variablen ableiten musst. Der Hintergrund ist der: