| Autor |
Nachricht |
QuantenZustand123
Gast
|
 QuantenZustand123 Verfasst am: 21. Nov 2020 15:09 Titel: Qubit-System in Bell-Basis QuantenZustand123 Verfasst am: 21. Nov 2020 15:09 Titel: Qubit-System in Bell-Basis |
 |
|
Meine Frage:
Hi,
eine Qubit System hat den allgemeinen Zustand:
 . Nun möchte Ich . Nun möchte Ich  in der Basis der Bell Zustände in der Basis der Bell Zustände  angeben. angeben.
Ich habe einfach mal mit dem ersten Teil angefangen:
 + b(\left| \Phi^- \right>) = a\frac{1}{\sqrt{2}} \left| 00 \right> + b \frac{1}{\sqrt{2}} \left| 00 \right> = (a+b) \frac{1}{\sqrt{2}} \left| 00 \right>)
-----------------------------------------------
Sei
 : :
 \frac{1}{\sqrt{2}} \left| 00 \right>)
z.B.
 , , 
Also  in der Bell Basis lautet dann: in der Bell Basis lautet dann:
 + \frac{1}{\sqrt{2}}(\left| \Phi^- \right>))
-----------------------------------------------
Ich habe das mal für alle vier Zustände gemacht, dann komme ich auf:
 + b(\left| \Phi^- \right>))
 + d(\left| \Psi^- \right>))
 - f(\left| \Psi^- \right>))
 - h(\left| \Phi^- \right>))
-----------------------------------------------
Wenn ich jetzt den allgemeinen Zustand des zwei Qubit Systems in der Bell Basis angeben möchte, würde ich jetzt einfach folgendes tun:
 + b(\left| \Phi^- \right>) + c(\left| \Psi^+ \right>) + d(\left| \Psi^- \right>) + e(\left| \Psi^+ \right>) - f(\left| \Psi^- \right>) + g(\left| \Phi^+ \right>) - h(\left| \Phi^- \right>))
Man könnte das jetzt noch etwas zusammen fassen, aber im Wesentlichen müsste es das doch gewesen sein, oder?
Danke, für kommende Antworten! 
Meine Ideen:
-- |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 21. Nov 2020 18:49 Titel: Re: Qubit System in Bell Basis index_razor Verfasst am: 21. Nov 2020 18:49 Titel: Re: Qubit System in Bell Basis |
 |
|
| QuantenZustand123 hat Folgendes geschrieben: | Meine Frage:
eine Qubit System hat den allgemeinen Zustand:
 . .
|
Ich vermute hierin steckt ein Schreibfehler und der Koeffizient vor  soll eigentlich soll eigentlich 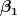 sein. sein.
| QuantenZustand123 hat Folgendes geschrieben: |
 + b(\left| \Phi^- \right>) + c(\left| \Psi^+ \right>) + d(\left| \Psi^- \right>) + e(\left| \Psi^+ \right>) - f(\left| \Psi^- \right>) + g(\left| \Phi^+ \right>) - h(\left| \Phi^- \right>))
Man könnte das jetzt noch etwas zusammen fassen, aber im Wesentlichen müsste es das doch gewesen sein, oder?
|
Nein, erstens hast du nun 8 Koeffizienten a,b,c,d,e,f,g,h für vier Basisvektoren. Das sind also vier zuviel. Zweitens erkenne ich nicht, daß du einen Zusammenhang zu den Koeffizienten  der ursprünglichen Basis hergestellt hast. Das ist aber genau die Aufgabe. (Deine Rechenung für der ursprünglichen Basis hergestellt hast. Das ist aber genau die Aufgabe. (Deine Rechenung für  verwendet außerdem nur zwei Elemente der Bell-Basis. Müßten es nicht vier sein?) verwendet außerdem nur zwei Elemente der Bell-Basis. Müßten es nicht vier sein?)
Das prinzipielle Vorgehen wäre, daß du z.B. ) mit mit 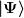 mutiplizierst mutiplizierst
.)
Das ist der Koeffizient vor  in der gesuchten Entwicklung. Analog verfährst du mit den anderen Basisvektoren. in der gesuchten Entwicklung. Analog verfährst du mit den anderen Basisvektoren. |
|
 |
QuantenZustand123
Gast
|
 QuantenZustand123 Verfasst am: 22. Nov 2020 18:10 Titel: QuantenZustand123 Verfasst am: 22. Nov 2020 18:10 Titel: |
 |
|
Danke index_razor! 
Du hast völlig Recht mit dem was du sagst! Der "Trick" über das Skalarprodukt ist sehr schön! Ich bin auch auf das gleiche Ergebnis gekommen wie du. Statt des Skalarproduktes habe ich einen Koeffizienten Vergleich gemacht 
Danke! |
|
 |
|
|