| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 07. Jun 2020 17:07 Titel: TomS Verfasst am: 07. Jun 2020 17:07 Titel: |
 |
|
Noch zwei Beispiele:
Man betrachte nicht-linear sigma-Modelle, Skyrme-Modelle sowie verallgemeinerte chiral-effective theories. Dabei verwendet man zunächst eine klassische Soliton-Lösung U_0(x) im 1-Nukleon Sektor, kollektive Koordinaten für deren Rotation A(t) sowie Translation X(t), sowie Fluktuationen
)
d.h. Pionen im Soliton-Background:
 = A \, \sqrt{U_0} \, e^{i\tau^a\pi^a} \, \sqrt{U_0} \, A^\dagger)
Die Quantisierung der Pionen erfolgt somit im 1-Nukleon-Sektor. Den Lagrangian entwickelt man bis zur gewünschten Ordnung in den pi. Die Soliton-Lösung kann numerisch bestimmt werden; es handelt sich letztlich um eine Funktion f(r). Die Fluktuationen können nur numerisch behandelt werden (aus ihnen folgen z.B. die Streuphasen zur Pion-Nukleon-Streuung; das ist jedoch lediglich relativistische Quantenmechanik).
Die quadratische Ordnung in pi liefert 1-Loop-Korrekturen zur Baryon-Masse, zum Radius, zur axialen Kopplung sowie zu elektrischen und magnetischen Momenten sowie Formfaktoren. In höherer Ordnung erwartet man Korrekturen zur Elektro-Pion-Produktion sowie zur Pion-Nukleon-Streuung; ich weiß nicht, ob das schon berechnet wurde.
Zur Berechnung der eichfeldabhängigen axialen Anomalie
 )
mittels der Fujikawa-Methode betrachtet man

die Eigenfunktionen der kovarianten Ableitung
 \, u_\lambda = 0)

sowie das Verhalten des Maßes unter der axialen Transformationen

Der Index des Dirac-Operators entspricht gerade der Differenz der Anzahl linkshändiger und rechtshändiger Eigenfunktionen.
Obwohl dies üblicherweise im Pfadintegralformalismus durchgeführt wird, existieren auch Berechnungen im kanonischen Formalismus, die eine Quantisierung der Fermionfelder mittels der o.g. Eigenfunktionen der kovarianten Ableitung nutzen, d.h. keine ebenen Wellen und keinen Bezug zur freien Theorie
https://lib-extopc.kek.jp/preprints/PDF/2000/0036/0036729.pdf
Sorry, ein besseres Paper habe ich nicht gefunden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Jun 2020 20:12 Titel: index_razor Verfasst am: 09. Jun 2020 20:12 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Hallo index_razor,
danke für deinen Beitrag, und sorry für meine sehr späte Antwort.
|
Keine Ursache, ich habe es ja nicht eilig.
| Zitat: |
Ja, wie vermutet lag das Missverständnis (implizit) im Bezug zur freien Theorie begründet.
Du schreibst
| index_razor hat Folgendes geschrieben: | Vielleicht ist das einfach deine Definition von  . Allerdings frage ich mich dann wie du das rechtfertigen willst. Erzeuger und Vernichter definiert man ja nicht einfach als "irgendeine Linearkombination aus Feld und kanonisch konjugiertem". Sie müssen doch die Randbedingungen . Allerdings frage ich mich dann wie du das rechtfertigen willst. Erzeuger und Vernichter definiert man ja nicht einfach als "irgendeine Linearkombination aus Feld und kanonisch konjugiertem". Sie müssen doch die Randbedingungen
 = a_{k,\pm}^\dagger )
erfüllen, wobei auf der rechten Seite Erzeuger von Streuzuständen stehen, die einen klar definierten Zusammenhang zu den Eigenzuständen des freien Hamiltonians haben. |
Das ist richtig, wenn ich einen mit der freien Theorie „verbundenen Sektor“ des vollen Hilbertraumes betrachte. Dann muss es möglich sein, diese Relation für die Erzeuger und Vernichter zu berücksichtigen.
|
Ich habe mich hier ein bißchen dumm ausgedrückt, deswegen muß ich wohl wieder etwas klarstellen. Ich schrieb jedoch absichtlich nur, daß  "einen klar definierten Zusammenhang" zu den Eigenzuständen der freien Theorie haben. Sie erzeugen aber trotzdem Streuzustände, also Eigenzustände der wechselwirkenden Theorie. Ich habe bisher immer vorausgesetzt, daß Störungstheorie und Diracbild irgendwie sinnvoll anwendbar sind, weil die Wechselwirkung das Spektrum der Theorie nicht dramatisch ändert. Deswegen habe ich nicht klar unterschieden zwischen Eigenzuständen der freien Theorie und solchen, die lediglich die Dispersionsrelation "einen klar definierten Zusammenhang" zu den Eigenzuständen der freien Theorie haben. Sie erzeugen aber trotzdem Streuzustände, also Eigenzustände der wechselwirkenden Theorie. Ich habe bisher immer vorausgesetzt, daß Störungstheorie und Diracbild irgendwie sinnvoll anwendbar sind, weil die Wechselwirkung das Spektrum der Theorie nicht dramatisch ändert. Deswegen habe ich nicht klar unterschieden zwischen Eigenzuständen der freien Theorie und solchen, die lediglich die Dispersionsrelation  erfüllen. Letztere impliziert, daß das Feld, welches diese Teilchen erzeugt, die "freie" Klein-Gordon-Gleichung erfüllen. Letztere impliziert, daß das Feld, welches diese Teilchen erzeugt, die "freie" Klein-Gordon-Gleichung \phi = 0) erfüllt. Allerdings ist m hier die physikalische, also renormierte, Masse und enthält somit Terme aus der wechselwirkenden Theorie. erfüllt. Allerdings ist m hier die physikalische, also renormierte, Masse und enthält somit Terme aus der wechselwirkenden Theorie.
| Zitat: |
D.h. jedoch nur, dass man sich asymptotisch auf die freie Theorie bezieht, und dass man deswegen sinnvollerweise Funktionensysteme betrachtet, die zumindest asymptotisch zu ebenen Wellen führen.
|
Nach meinem Verständnis ergibt das Anwenden von Erzeugern auf den Vakuumzustand ein Element aus dem Einteilchen-Sektor der Theorie und n-maliges Anwenden einen Fockraumzustand zur Teilchenzahl n. Das ist meine Definition von "Erzeuger".
Mein Hauptproblem ist, daß ich nicht verstehe, was deine Operatoren  überhaupt mit dem Einteilchensektor zu tun haben sollen. Ich denke es kann im allgemeinen kein derartig simpler Zusammenhang zwischen den Fockraumzuständen und den Heisenbergfeldern bestehen, wie du ihn vorschlägst. Die Rekonstruktion der Einteilchenzustände erfordert normalerweise Kenntnis der Spektralfunktion der Theorie. Der Heisenbergoperator wird ja im allgemeinen nichtverschwindenden Überlapp mit Mehrteilchenzuständen besitzen überhaupt mit dem Einteilchensektor zu tun haben sollen. Ich denke es kann im allgemeinen kein derartig simpler Zusammenhang zwischen den Fockraumzuständen und den Heisenbergfeldern bestehen, wie du ihn vorschlägst. Die Rekonstruktion der Einteilchenzustände erfordert normalerweise Kenntnis der Spektralfunktion der Theorie. Der Heisenbergoperator wird ja im allgemeinen nichtverschwindenden Überlapp mit Mehrteilchenzuständen besitzen
|0\rangle \neq 0.)
Wenn man aus  einen Erzeuger für Einteilchenzustände rekonstruieren will, muß man eine Wellenfunktion einen Erzeuger für Einteilchenzustände rekonstruieren will, muß man eine Wellenfunktion ) wählen, deren Träger im 4-Impulsraum um einen einzelnen diskreten Eigenwert von H konzentriert ist wählen, deren Träger im 4-Impulsraum um einen einzelnen diskreten Eigenwert von H konzentriert ist
 = \int\dd^4 y f(y-x) \phi(y) )
(Dies ist im vorliegenden Fall noch mit der Komplikation verbunden, daß es sich anscheinend um ein masseloses Feld handelt.) Unter den eingangs erwähnten Annahmen, daß es im wesentlichen um eine Theorie eines einzelnen skalaren Teilchens mit Masse m handelt, folgt hieraus der Erzeuger dieses Teichens
}} e^{i(\vec{k}\cdot\vec{x} - E(\vec{k})t)}\overset{\leftrightarrow}{\partial_t}\tilde{\phi}_1(x) = a^\dagger_{\pm,\vec{k}}.)
Man muß also zumindest wissen, wo das kontinuierliche Spektrum von H anfängt. Keine derartige Überlegung geht in dein Argument ein, was seltsam ist.
Und dabei haben wir noch nicht einmal in betracht gezogen, daß die Theorie eventuell Bindungszustände aus mehreren  -Teilchen zuläßt, die ebenfalls im Einteilchensektor landen, oder daß möglicherweise gar keine freien -Teilchen zuläßt, die ebenfalls im Einteilchensektor landen, oder daß möglicherweise gar keine freien  -Teilchen unter den physikalischen Zuständen existieren. In diesem Fall müssen die Erzeuger, wenn überhaupt, aus Produkten von -Teilchen unter den physikalischen Zuständen existieren. In diesem Fall müssen die Erzeuger, wenn überhaupt, aus Produkten von  -Operatoren (und eventuell deren Ableitungen -Operatoren (und eventuell deren Ableitungen  ) zusammengebaut werden und nicht aus irgendeiner Linearkombination. ) zusammengebaut werden und nicht aus irgendeiner Linearkombination.
Ich halte es nicht für wahrscheinlich, daß eine der letzten beiden Optionen zutrifft, aber sicher bin ich mir nicht. Und dein Argument läßt es so aussehen, als sei das nicht mal Grund für irgendwelche Bedenken.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Das war von dir aber offenbar nicht so gemeint, und meine Interpretation deiner  paßt wohl auch nicht dazu, daß paßt wohl auch nicht dazu, daß  einfach irgendein Funktionensystem ohne jegliche Verbindung zu den Feldgleichungen ist. Dadurch werden sie aber m.E. für die Quantisierung auch erstmal nutzlos. einfach irgendein Funktionensystem ohne jegliche Verbindung zu den Feldgleichungen ist. Dadurch werden sie aber m.E. für die Quantisierung auch erstmal nutzlos. |
Meine Interpretation ist wohl allgemeiner, aber sie ist deswegen für die Quantisierung sicher nicht nutzlos. Und das Funktionensystem wird in der Praxis sicher irgendeine Beziehung zu den Feldgleichungen haben, wenn auch nicht zwingend eine zur freien Theorie.
|
Es gibt einen Zusammenhang zwischen den Einteilchenzuständen der Theorie und den Lösungen der Feldgleichung \Phi = 0) . Ich denke dieser Zusammenhang ist für die Quantisierung fundamental (abgesehen von den Komplikationen, die ich oben erwähnt habe) und nicht lediglich eine Frage der Zweckmäßigkeit. Genau die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. Vielleicht sollte man diese Gleichung nicht als "freie" Gleichung bezeichnen, wie ich es getan habe. (Siehe dazu unten.) . Ich denke dieser Zusammenhang ist für die Quantisierung fundamental (abgesehen von den Komplikationen, die ich oben erwähnt habe) und nicht lediglich eine Frage der Zweckmäßigkeit. Genau die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. Vielleicht sollte man diese Gleichung nicht als "freie" Gleichung bezeichnen, wie ich es getan habe. (Siehe dazu unten.)
| Zitat: |
| index_razor hat Folgendes geschrieben: | ... weil ich sie für notwendig halte, da sie die Definition des Fockraums impliziert. Das siehst du offenbar anders. Sorry für die Verwirrung.
Was mich allerdings wundert ist, daß du bis jetzt keine Bemerkung dazu machst, was deine Linearkombinationen von  überhaupt als "Erzeuger und Vernichter" qualifiziert. Wie kommst du darauf, daß wiederholtes anwenden überhaupt als "Erzeuger und Vernichter" qualifiziert. Wie kommst du darauf, daß wiederholtes anwenden  den kompletten Fockraum der Theorie aufspannt? Nach deiner Konstruktion erscheint mir nicht mal offensichtlich, wie der Fockraum überhaupt aussehen könnte. Ich finde das ist ein Punkt, auf den du bei deiner Diskussion der Quantisierung unbedingt eingehen solltest. den kompletten Fockraum der Theorie aufspannt? Nach deiner Konstruktion erscheint mir nicht mal offensichtlich, wie der Fockraum überhaupt aussehen könnte. Ich finde das ist ein Punkt, auf den du bei deiner Diskussion der Quantisierung unbedingt eingehen solltest. |
Nach meinem Verständnis folgt eine Fockraumstruktur formal alleine aus den Vertauschungsrelationen der Erzeuger und Vernichter sowie aus der Vollständigkeit des Funktionensystems.
|
Nein, das kann nicht stimmen. Die Fockraumstruktur kann doch nicht unabhängig von der Wechselwirkung sein. Wenn es stimmte, was du sagst, hätten Elektronen und Quarks im wesentlichen dieselben Zustände, denn ihre Vertauschungsrelationen sind eindeutig durch ihren Spin bestimmt, der für beide Teilchen gleich ist.
Die stabilen Impulseigenzustände der QCD sind aber Protonen (plus Neutronen und Pionen, wenn man von der schwachen Wechselwirkung absieht), die also allenfalls durch farbneutrale Produkte von 3 (oder 2) wechselwirkenden Quarkfeldern interpoliert werden. Im Gegensatz dazu enthalten die Einteilchenzustände der wechselwirkenden QED immer noch einzelne ("gedresste") Elektronen (ziemlich ähnlich zu deinem Beispiel unten), also die Quanten eines elementaren Feldes.
Die Fockraumstruktur aus den wechselwirkenden Feldern zu rekonstruieren ist im allgemeinen eine ziemlich diffizile Angelegenheit. Ich bin mir aber nicht mal sicher, was du als "Einteilchenhilbertraum" auffaßt. Es scheinen nicht die üblichen irreduziblen Darstellungen der Poincare-Gruppe zu sein. Ansonsten landest du ja bei der Feldgleichung
\psi_\ell = 0)
für die Komponente jedes Feldes welche stabile 1-Teilchen-Zustände erzeugt.
| Zitat: |
Damit ist noch nicht gewährleistet, dass dieser Fockraum (bis auf unitäre Äquivalenz) eindeutig und für das konkrete Modell = den konkreten Hamiltonian sinnvoll oder nützlich ist (und dabei lassen wir mal die Fragestellung außen vor, ob der Hamiltonian sowie weitere Operatoren überhaupt mathematisch wohldefiniert sind).
Mir ist bewusst, dass unterschiedliche Funktionensysteme zu unterschiedlichen Fockräumen führen können und dass diese gerade nicht zwingend unitär äquivalent sein müssen (Haagsches Theorem); m.a.W.: möglicherweise benötigt man für verschiedene Sektoren des Hilbertraumes unterschiedliche Fockräume, und möglicherweise ist das für eine konkrete Theorie ein echter Defekt (wir verstehen die Quantenfeldtheorie heute noch nicht besser).
|
Ich verstehe nicht was das bedeuten soll. Der Fockraum der Theorie ist die Summe aus (symmetrisierten) Produkten des kompletten Einteilchenhilbertraums. Er enthält also per Definition alle Sektoren des Hilbertraums. Verschiedene Sektoren müssen natürlich nicht zu unitär äquivalenten Darstellungen gehören. Das ist ja bereits die Situation, wenn die Theorie Teilchen verschiedenen Spins enthält. Also leuchtet mir nicht ganz ein, was hier auf irgendeinen Defekt hindeuten soll.
Was deine Funktionensysteme betrifft, verstehe ich aber gar nicht, wieso sie überhaupt auf einen Fockraum führen sollen. Das übliche Vorgehen bei zweiter Quantisierung ist ja ungefähr, den Einteilchensektor mit komplexen Lösungen der Feldgleichungen positiver Frequenz zu identifizieren. Das müssen vielleicht nicht unbedingt ebene Wellen sein.
Aber ich sehe nicht, wie diese Prozedur funktionieren soll, wenn die Gleichungen nicht linear sind. Dann bildet die Lösungsmenge nicht mal einen Vektorraum, wo soll also der Hilbertraum herkommen?
| Zitat: |
Einige Beispiele:
In der 1+1 dimensionalen QED auf dem Kreis kann man das elektrische Feld in der Weyl-Eichung bis auf einen dynamischen Zero-Mode a(t) vollständig ausintegrieren
 - m] \, \psi = 0 )
 = \tilde{A}_1(x,t) + a(t) )
 \to \exp\left[ie\int^x \tilde{A}\right] \, \psi(x,t) )
Damit erhält man „dressed Fermions“, wobei der Fluktuationsanteil des Eichfeldes in das Fermionfeld absorbiert wird; der Fluktuationsanteil ist durch den Constraint des Gaußschen Gesetz vollständig festgelegt und daher nicht dynamisch. Der Fockraum wird dann mittels ebener Wellen für die dressed Fermions konstruiert; freie Fermionfelder sind in dieser Formulierung aufgrund des unbekannten Eichfeldanteils nicht explizit bekannt.
|
Das sehe ich natürlich ein. Die Bezeichnung "freie Felder" war von mir nicht korrekt gewählt. In der gewöhnlichen skalaren QFT im 3+1-dimensionalen Minkowskiraum meine ich damit irgendein Feld, welches die Gleichung \Phi = 0) erfüllt. Hierbei ist erfüllt. Hierbei ist 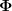 ein Heisenbergfeld der wechselwirkenden Theorie oder ein Produkt aus solchen Feldern und ein Heisenbergfeld der wechselwirkenden Theorie oder ein Produkt aus solchen Feldern und 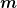 ein diskreter Eigenwert des vollen Hamiltonians. "Frei" habe ich das oben nur genannt, weil kein Quellterm auf der rechten Seite steht. Auch Verallgemeinerungen sind denkbar z.B. ein diskreter Eigenwert des vollen Hamiltonians. "Frei" habe ich das oben nur genannt, weil kein Quellterm auf der rechten Seite steht. Auch Verallgemeinerungen sind denkbar z.B.
\psi = 0)
für Fermionen in einem äußeren (nichtdynamischen) Feld. Das ist wohl die Essenz deines Beispiels hier. Auch hier sehe ich kein besonderes Problem mit der Quantisierung. Die Gleichung ist linear und obwohl die Lösungen für 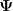 also von also von  abhängen, bilden sie offensichtlich einen Vektorraum. abhängen, bilden sie offensichtlich einen Vektorraum.
Aber welchen Bezug hat dieses oder eines deiner anderen Beispiele zu der vorliegenden Theorie oder zu deiner Behauptung  repräsentiere Erzeugungsoperatoren auf ihrem Fockraum? repräsentiere Erzeugungsoperatoren auf ihrem Fockraum? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 14. Jun 2020 17:36 Titel: TomS Verfasst am: 14. Jun 2020 17:36 Titel: |
 |
|
Zunächst: evtl. ist es besser, wir machen nochmal einen Reset und starten unten mit *)
| index_razor hat Folgendes geschrieben: | | Nach meinem Verständnis ergibt das Anwenden von Erzeugern auf den Vakuumzustand ein Element aus dem Einteilchen-Sektor der Theorie und n-maliges Anwenden einen Fockraumzustand zur Teilchenzahl n. Das ist meine Definition von "Erzeuger". |
Diese zunächst rein algebraische Eigenschaft ist auch mein Verständnis, nur muss man dazu weder ein Funktionensystem noch eine Dispersionsrelation auszeichnen. Die Operatoren mit geeigneten Kommutatoren sind m.E. ausreichend.
| index_razor hat Folgendes geschrieben: | Mein Hauptproblem ist, daß ich nicht verstehe, was deine Operatoren  überhaupt mit dem Einteilchensektor zu tun haben sollen. Ich denke es kann im allgemeinen kein derartig simpler Zusammenhang zwischen den Fockraumzuständen und den Heisenbergfeldern bestehen, wie du ihn vorschlägst. Die Rekonstruktion der Einteilchenzustände erfordert normalerweise Kenntnis der Spektralfunktion der Theorie. überhaupt mit dem Einteilchensektor zu tun haben sollen. Ich denke es kann im allgemeinen kein derartig simpler Zusammenhang zwischen den Fockraumzuständen und den Heisenbergfeldern bestehen, wie du ihn vorschlägst. Die Rekonstruktion der Einteilchenzustände erfordert normalerweise Kenntnis der Spektralfunktion der Theorie. |
Ich denke, wir haben einen unterschiedlichen Begriff von Ein- bzw. n-Teilchenzuständen. Bei mir sind dies zunächst einfach Zustände, die die algebraisch definierten Erzeuger erzeugen und die der algebraisch definierte Teilchenzahloperator „zählt“.
Evtl. missverstehen wir uns einfach.
In der QCD verwendet man für die Konstruktion des Fockraums freier oder näherungsweise freier Quarks z.B. ebene Wellen; wir wissen jedoch, dass gerade diese Teilchen – freie Quarks – im IR-Sektor nicht existieren. Und da, wo sie existieren, erhalten diese Zustände einen nicht-triviale Beitrag von der Renormierung der Masse, d.h. wir verwenden sozusagen die falschen ebenen Wellen. Für mögliche Fockräume freier oder näherungsweise freier Gluonen erhalten wir – je nach Eichung – unterschiedliche Ergebnisse. In einer transversalen Eichung existieren zwei physikalische Felder, in anderen Eichungen existieren auch Fockraumzustände zu longitudinalen und damit unphysikalischen Gluonen sowie zusätzlich Fockraumzustände für Fadeev-Popov-Geister. In einem klassischen Background wie einem Instanton-Vakuum würden sich die propagierenden Einteilchenzustände nicht mehr auf diese freien Felder beziehen.
Auch im Falle der Dualität des 2-dim. Sine-Gordon-Modells selbstwechselwirkender Skalarfelder mit dem 2-dim. Thirring-Modells selbstwechselwirkender Fermionen gibt es nicht den Fockraum. Die fundamentalen Fermionen des Thirring-Modells entsprechen den Solitonen des Sine-Gordon-Modells, d.h. die näherungsweise freien fermionischen Einteilchenzustände des Thirring-Modells entsprechen Vielteilchenzuständen im bosonischen Fockraum eines freien Klein-Gordon-Modells.
Da ich derartige Diskussionen bzgl. der Lösungen der Theorie zum Zeitpunkt der Quantisierung noch gar nicht führen kann, lasse ich ganz allgemein zu, dass jedes System von Operatoren  bzw. die daraus abgeleiteten bzw. die daraus abgeleiteten  mit geeigneten Kommutatoren einen möglichen Fockraum definiert. mit geeigneten Kommutatoren einen möglichen Fockraum definiert.
Ich sehe immer noch nicht, was mich mathematisch daran hindern sollte.
| index_razor hat Folgendes geschrieben: | Es gibt einen Zusammenhang zwischen den Einteilchenzuständen der Theorie und den Lösungen der Feldgleichung \Phi = 0) . Ich denke dieser Zusammenhang ist für die Quantisierung fundamental (abgesehen von den Komplikationen, die ich oben erwähnt habe) und nicht lediglich eine Frage der Zweckmäßigkeit. Genau die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. . Ich denke dieser Zusammenhang ist für die Quantisierung fundamental (abgesehen von den Komplikationen, die ich oben erwähnt habe) und nicht lediglich eine Frage der Zweckmäßigkeit. Genau die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. |
Moment.
Meinst du jetzt mit Einteilchenzuständen solche, die du direkt aus Linearkombinationen von  – ggf. nach Massenrenormierung – ableitest? Also im wesentlichen wieder die Struktur der freien Theorie? Das entspräche deiner Aussage – ggf. nach Massenrenormierung – ableitest? Also im wesentlichen wieder die Struktur der freien Theorie? Das entspräche deiner Aussage | Zitat: | | die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. |
Oder meinst du | Zitat: | | die stabilen Impulseigenzustände der QCD – Protonen plus Neutronen und Pionen – die allenfalls durch farbneutrale Produkte von wechselwirkenden Quarkfeldern interpoliert werden. |
Letztere haben zunächst nichts mit dem Fockraum zu tun, der im Zuge der Quantisierung konstruiert wird und in dem die n-Teilchen-Zustände von z.B. asymptotisch freien Quarks und Gluonen leben.
Wie Mesonen und Baryonen im o.g. Fockraum definiert werden ist bis heute im wesentlichen unbekannt; und wie direkt ein physikalischer Fockraum inklusive der Erzeuger und Vernichter dieser physikalischen Zustände der Mesonen und Baryonen konstruiert wird, ebenfalls. Ich wollte an keiner Stelle andeuten, dass ich irgendetwas über eine Fockraumstruktur der Lösungen der QCD aussagen kann; ich wüsste noch nicht mal, ob es eine solche Fockraumstruktur gibt oder überhaupt geben muss (wenn es sie gibt, kann sie nicht unitär äquivalent zum Fockraum der freien Theorie sein).
Und ein | Zitat: | Zusammenhang zwischen den [physikalischen] Einteilchenzuständen [wie Nukleonen] und den Lösungen der Feldgleichung \Phi = 0) ” ” |
ist im Falle der QCD unbekannt, d.h. die Aussage | Zitat: | | dieser Zusammenhang ist für die Quantisierung fundamental |
kann nicht richtig sein, und | Zitat: | | die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. |
kann sich demnach doch nur auf den Fockraum der freien oder asymptotisch freien Theorie beziehen.
| index_razor hat Folgendes geschrieben: | | Zitat: | Nach meinem Verständnis folgt eine Fockraumstruktur formal alleine aus den Vertauschungsrelationen der Erzeuger und Vernichter sowie aus der Vollständigkeit des Funktionensystems.
|
Nein, das kann nicht stimmen. Die Fockraumstruktur kann doch nicht unabhängig von der Wechselwirkung sein. Wenn es stimmte, was du sagst, hätten Elektronen und Quarks im wesentlichen dieselben Zustände, denn ihre Vertauschungsrelationen sind eindeutig durch ihren Spin bestimmt, der für beide Teilchen gleich ist. |
Zunächst ist das – bis auf Color und Flavor – für die fermionischen Fockräume der freien Theorien tatsächlich der Fall; die Fockräume sind identisch. Im Falle der QED bleibt diese Struktur bis auf Renormierung im Wesentlichen erhalten, im Falle der QCD ist es komplizierter: man verwendet zwar den Fockraum der freien Theorie zur Quantisierung, allerdings bleibt dieser nur im asymptotisch freien Sektor der Theorie physikalisch relevant; im IR-Sektor der Baryonen und Mesonen ist eine Fockraumstruktur dieser physikalischen Freiheitsgrade unbekannt.
| index_razor hat Folgendes geschrieben: | | Ich bin mir aber nicht mal sicher, was du als "Einteilchenhilbertraum" auffaßt. Es scheinen nicht die üblichen irreduziblen Darstellungen der Poincare-Gruppe zu sein. |
Ein Einteilchenhilbertraum wird mittels Operatoren konstruiert die die entsprechenden Vertauschungsrelationen erfüllen (aber evtl. meine ich hier etwas anderes als du; sprichst du hier von Mesonen und Baryonen?)
Wenn ich dazu ebene Wellen benutze, dann erhalte ich direkt die üblichen irreduziblen Darstellungen der Poincare-Gruppe.
Wenn ich – wie z.B. im Falle des Sine-Gordon-Modells – Streuzustände auf einem Soliton-Background nutze, erhalte ich nicht diese Darstellungen der Poincare-Gruppe.
Wenn ich – wie im Falle der QCD – ebene Wellen und damit den Fockraum der freien Theorie zur Quantisierung benutze, dann erwarte ich zwar wiederum irreduzible Darstellungen der Poincare-Gruppe für Mesonen und Baryonen, aber diese haben nichts mit den Darstellungen für Quarks und Gluonen zu tun, die mir die freie Theorie geliefert hat (gleiches gilt für die Flavor-Multiplets).
*) Ich versuche meine Aussage – am Beispiel QCD – nochmal neu zu formulieren:
Die kanonische Quantisierung auf Basis der fundamentalen Felder der Quarks und Gluonen sowie mittels ebener Wellen liefert (modulo Eichsymmetrie) den Fockraum der freien Theorie, noch ohne Kenntnis weiterer Strukturen oder Operatoren. Dieser Fockraum bleibt physikalisch relevant für den asymptotisch freien Sektor, der die “renormierten Streuzustände” der fundamentalen Felder enthält.
Dieser Fockraum ist physikalisch irrelevant im IR-Sektor der gebundene Zustände, d.h. für Mesonen und Baryonen. Für letztere ist m.W.n. keine explizite Fockraumstruktur bekannt, d.h. man kann zwar so etwas wie

für ein Nukleon mit Impuls k, Spin s und Flavor f schreiben, kennt dafür jedoch m.W.n. keine aus den fundamentalen Feldern ableitbare Darstellung von Erzeugern und Vernichtern dieser effektiven Freiheitsgrade, die – zumindest näherungsweise – die korrekten Vertauschungsrelationen erfüllen und somit einen Fockraum definieren würden. Man kennt im Rahmen der QCD noch nicht mal den physikalischen, nicht-perturbativen Vakuumzustand des IR-Sektors mit nicht-verschwindenden Kondensaten

D.h. der Fockraum der freien Theorie dient hier lediglich als mathematisches Werkzeug und hat nichts mit den physikalischen Lösungen der Theorie zu tun, also dem nicht-perturbativen Vakuum, den Mesonen, Baryonen usw. (außer dass man annimmt, man könne letztere im selben Fockraum konstruieren).
Insbs. verletzen die Fockraumzustände

wobei I =„Impuls k, Spin s, Flavor f, Color i“ umfasst, die zwingend notwendige Ladungsneutralität bzgl. SU(N)-Color

Meine Behauptung ist nun lediglich die folgende: gerade weil die Fockraumzustände der freien Theorie praktisch nichts mit den letztlich relevanten Zuständen der wechselwirkenden Theorie und damit den Lösungen = dem physikalischen Spektrum des Hamiltonians zu tun haben, existiert kein physikalisch zwingender Grund, für die Quantisierung gerade die ebenen Wellen der freien Theorie zu wählen; im asymptotisch freien Sektor ist das natürlich sinnvoll, im IR-Sektor dagegen irrelevant; jedes andere Funktionssystem ist prinzipiell zulässig. Und mit einem anderen Funktionssystem erhält man einen anderen – ich denke unitär äquivalenten – Fockraum; letzteres wäre zu zeigen.
EDIT:
Andere Funktionensysteme als ebene Wellen werden u.A. in der Festkörperphysik verwendet - Blochwellen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. Jun 2020 10:09 Titel: index_razor Verfasst am: 20. Jun 2020 10:09 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Zunächst: evtl. ist es besser, wir machen nochmal einen Reset und starten unten mit *)
|
Gut, fangen wir dort an. Ich fände es allerdings auch gut wenn du den Bogen zur ursprünglichen Frage nochmal spannen könntest, die ja verlangt, einen Hamiltonoperator durch Erzeuger und Vernichter auszudrücken. Aus deiner ganzen Argumentation scheint zu folgen, daß diese Frage eigentlich sinnlos ist, weil es unendlich viele triviale Lösungen gibt.
| Zitat: |
*) Ich versuche meine Aussage – am Beispiel QCD – nochmal neu zu formulieren:
Die kanonische Quantisierung auf Basis der fundamentalen Felder der Quarks und Gluonen sowie mittels ebener Wellen liefert der Fockraum der freien Theorie, noch ohne Kenntnis weiterer Strukturen oder Operatoren. Dieser Fockraum bleibt physikalisch relevant für den asymptotisch freien Sektor, der die “renormierten Streuzustände” der fundamentalen Felder enthält.
|
Warum wirfst du hier kanonische Quantisierung mit irgendwelchen "ebenen Wellen" durcheinander? Kanonische Quantisierung heißt nur: es gibt einen Hilbertraum mit Operatoren, die die kanonischen Vertauschungsrelationen erfüllen
, \pi(\vec{y}, t)] = i\delta(\vec{x}-\vec{y}).)
Das hat gar nichts mit "ebenen Wellen" zu tun. Es hat noch nicht einmal etwas mit einem Fockraum zu tun.
| Zitat: |
Dieser Fockraum ist physikalisch irrelevant im IR-Sektor der gebundene Zustände, d.h. für Mesonen und Baryonen. Für letztere ist m.W.n. keine explizite Fockraumstruktur bekannt, d.h. man kann zwar so etwas wie

für ein Nukleon mit Impuls k, Spin s und Flavor f schreiben, kennt dafür jedoch m.W.n. keine aus den fundamentalen Feldern ableitbare Darstellung von Erzeugern und Vernichtern dieser effektiven Freiheitsgrade, die – zumindest näherungsweise – die korrekten Vertauschungsrelationen erfüllen und somit einen Fockraum definieren würden. |
Ja, der aus freien Quarkfeldern konstruierbare Fockraum ist (außer als Näherung für hohe Energien) irrelevant. Und der relevante Fockraum kann nicht explizit aus Quarkfeldern konstruiert werden. Das bestreite ich nicht. Die Frage was man explizit konstruieren kann, ist für mich allerdings nicht von fundamentaler Bedeutung und so ziemlich alles was man im Falle der QCD explizit konstruieren kann, hat nicht viel mit der exakten Theorie zu tun und umgekehrt.
| Zitat: |
D.h. der Fockraum der freien Theorie dient hier lediglich als mathematisches Werkzeug und hat nichts mit den physikalischen Lösungen der Theorie zu tun, also dem nicht-perturbativen Vakuum, den Mesonen, Baryonen usw. (außer dass man annimmt, man könne letztere im selben Fockraum konstruieren).
|
Das nimmt man überhaupt nicht an und muß es auch nicht. Es ist sogar mit ziemlicher Sicherheit nicht derselbe Fockraum. Das ist eine Konsequenz aus Haags-Theorem. Vermutlich leben nicht mal nackte Quarks und Quarks mit renormierter Masse im selben Fockraum. (Reed, Simon beweisen, daß freie skalare Felder unterschiedlicher Masse zu nicht-äquivalenten Darstellung der kanonischen Vertauschungsrelationen gehören. Siehe Methods of Modern Mathematical Physics, Vol II, Abschnitt X.7)
Ich habe den Eindruck du hast eine irgendwie ambivalente Einstellung zu deinem Fockraum "freier Quarks". Einerseits scheinst du ihn für fundamental notwendig "für die Quantisierung" zu halten. Dann hat er wieder nichts mit den physikalischen Lösungen der Theorie zu tun. Und zum Schluß sollen die exakten Zustände doch irgendwie in ihm konstruierbar sein. Das paßt für mich irgendwie nicht zusammen.
| Zitat: |
Meine Behauptung ist nun lediglich die folgende: gerade weil die Fockraumzustände der freien Theorie praktisch nichts mit den letztlich relevanten Zuständen der wechselwirkenden Theorie und damit den Lösungen = dem physikalischen Spektrum des Hamiltonians zu tun haben, existiert kein physikalisch zwingender Grund, für die Quantisierung gerade die ebenen Wellen der freien Theorie zu wählen; im asymptotisch freien Sektor ist das natürlich sinnvoll, im IR-Sektor dagegen irrelevant; jedes andere Funktionssystem ist zulässig. |
Ich habe keine Ahnung was all das bedeuten soll.
Wenn die Fockraumzustände der freien Theorie sich wesentlich von der wechselwirkenden Theorie unterscheiden, muß man zur Definition eben die wechselwirkenden Felder zugrunde legen, wie z.B. in der Haag-Ruelle-Theorie. Andernfalls erhält man höchstens eine grobe Näherung, z.B. für hohe Energien (oder kurze Zeitskalen etc.) im Falle freier Quarks.
Die Wahl irgendeines anderen Funktionensystems macht hingegen aus der Theorie eines freien Quantenfeldes nicht eine mit wechselwirkenden Feldern. Insofern ist die Wahl vollkommen egal. Wegen der Lorentzinvarianz der Theorie ist es aber immer möglich freie Teilchen mit Feldern
 + e^{ipx}a(\vec{p})\right))
zu erzeugen. Daran ändert sich m.E. auch nicht viel, selbst wenn es sich um freie Teilchen in einer Theorie wechselwirkender Felder handelt.
| Zitat: | | Und mit einem anderen Funktionssystem erhält man einen anderen – ich denke unitär äquivalenten – Fockraum; letzteres wäre zu zeigen. |
Wenn man einen unitär äquivalenten Raum erhält, ergibt sich auch wieder eine freie Theorie. Wozu soll das ganze also gut sein?
***
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Nach meinem Verständnis ergibt das Anwenden von Erzeugern auf den Vakuumzustand ein Element aus dem Einteilchen-Sektor der Theorie und n-maliges Anwenden einen Fockraumzustand zur Teilchenzahl n. Das ist meine Definition von "Erzeuger". |
Diese zunächst rein algebraische Eigenschaft ist auch mein Verständnis, nur muss man dazu weder ein Funktionensystem noch eine Dispersionsrelation auszeichnen. Die Operatoren mit geeigneten Kommutatoren sind m.E. ausreichend.
|
Der Begriff "Einteilchenzustand" bezeichnet für gewöhnlich einen Eigenzustand des Operators  zu einem diskreten Eigenwert zu einem diskreten Eigenwert  . Daher kommt die Dispersionsrelation . Daher kommt die Dispersionsrelation  . (Allerdings muß es sich natürlich nicht gleichzeitig um einen Impulseigenzustand handeln.) . (Allerdings muß es sich natürlich nicht gleichzeitig um einen Impulseigenzustand handeln.)
| Zitat: |
| index_razor hat Folgendes geschrieben: | Mein Hauptproblem ist, daß ich nicht verstehe, was deine Operatoren  überhaupt mit dem Einteilchensektor zu tun haben sollen. Ich denke es kann im allgemeinen kein derartig simpler Zusammenhang zwischen den Fockraumzuständen und den Heisenbergfeldern bestehen, wie du ihn vorschlägst. Die Rekonstruktion der Einteilchenzustände erfordert normalerweise Kenntnis der Spektralfunktion der Theorie. überhaupt mit dem Einteilchensektor zu tun haben sollen. Ich denke es kann im allgemeinen kein derartig simpler Zusammenhang zwischen den Fockraumzuständen und den Heisenbergfeldern bestehen, wie du ihn vorschlägst. Die Rekonstruktion der Einteilchenzustände erfordert normalerweise Kenntnis der Spektralfunktion der Theorie. |
Ich denke, wir haben einen unterschiedlichen Begriff von Ein- bzw. n-Teilchenzuständen. Bei mir sind dies zunächst einfach Zustände, die die algebraisch definierten Erzeuger erzeugen und die der algebraisch definierte Teilchenzahloperator „zählt“.
|
Wenn das deine Auffassung ist, dann hättest du ja auch bei den ursprünglichen kanonischen Variablen  bleiben können. Wozu hast du dann überhaupt die Operatoren bleiben können. Wozu hast du dann überhaupt die Operatoren
| Zitat: |
)
)
|
definiert? Du hättest ja genauso gut


verwenden können. Damit wäre die ursprüngliche Aufgabe ja noch trivialer gewesen. Deine Interpretation von Erzeugern und Vernichtern ist ja so abstrakt, das man praktisch nicht mehr machen muß, als  und und 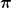 nach irgendeinem vollständigen Funktionensystem zu entwickeln und einzusetzen. nach irgendeinem vollständigen Funktionensystem zu entwickeln und einzusetzen.
| Zitat: | Für mögliche Fockräume freier oder näherungsweise freier Gluonen erhalten wir – je nach Eichung – unterschiedliche Ergebnisse. In einer transversalen Eichung existieren zwei physikalische Felder, in anderen Eichungen existieren auch Fockraumzustände zu longitudinalen und damit unphysikalischen Gluonen sowie zusätzlich Fockraumzustände für Fadeev-Popov-Geister.
|
Ich rede übrigens nur von den physikalischen Zuständen, also keine Geister und keine Zustände negativer Norm. Dieser Fockraum ist eichunabhängig.
| Zitat: |
In einem klassischen Background wie einem Instanton-Vakuum würden sich die propagierenden Einteilchenzustände nicht mehr auf diese freien Felder beziehen.
|
Nach deiner Definition kann so ziemlich alles als "Einteilchenzustand" bezeichnet werden. Insofern ist diese Aussage schwer zu beurteilen.
| Zitat: |
Auch im Falle der Dualität des 2-dim. Sine-Gordon-Modells selbstwechselwirkender Skalarfelder mit dem 2-dim. Thirring-Modells selbstwechselwirkender Fermionen gibt es nicht den Fockraum. Die fundamentalen Fermionen des Thirring-Modells entsprechen den Solitonen des Sine-Gordon-Modells, d.h. die näherungsweise freien fermionischen Einteilchenzustände des Thirring-Modells entsprechen Vielteilchenzuständen im bosonischen Fockraum eines freien Klein-Gordon-Modells.
|
Das mag zwar sein. Ich verstehe aber ehrlich gesagt nicht, warum wir in diesem Zusammenhang Eigenschaften des Sine-Gordon-Modells diskutieren. (Was nicht heißen soll, daß ich deine Bemerkungen dazu uninteressant finde.) Nach deiner eigenen Auffassung gibt es aber in jeder Theorie so viele unterschiedliche Fockräume wie Linearkombinationen der Felder, die die Vertauschungsrelationen  erfüllen. Das ist völlig unabhängig von irgendeiner Dualität oder Wechselwirkung. erfüllen. Das ist völlig unabhängig von irgendeiner Dualität oder Wechselwirkung.
Ich selbst bin auch nicht der Meinung, daß es eine eindeutige Fockraumdarstellung der Theorie geben muß. (Und hoffe ich habe das auch nirgendwo behauptet.) Soweit ich weiß kann es durchaus mehrere nicht-äquivalente Darstellungen geben, die jeweils in bestimmten Näherungen relevant sind. Es kann auch sein, daß der komplette Hilbertraum der Theorie überhaupt kein Fockraum ist.
| Zitat: |
Da ich derartige Diskussionen bzgl. der Lösungen der Theorie zum Zeitpunkt der Quantisierung noch gar nicht führen kann, lasse ich ganz allgemein zu, dass jedes System von Operatoren  bzw. die daraus abgeleiteten bzw. die daraus abgeleiteten  mit geeigneten Kommutatoren einen möglichen Fockraum definiert. mit geeigneten Kommutatoren einen möglichen Fockraum definiert.
Ich sehe immer noch nicht, was mich mathematisch daran hindern sollte.
|
Und ich sehe da keinerlei Zusammenhang. Es gibt viele Fragen in Bezug auf wechselwirkende Quantenfelder, die wir weder bei noch lange Zeit nach der Quantisierung beantworten können. Was soll die Definition von beliebigen Fockräumen da helfen?
| Zitat: |
| index_razor hat Folgendes geschrieben: | Es gibt einen Zusammenhang zwischen den Einteilchenzuständen der Theorie und den Lösungen der Feldgleichung \Phi = 0) . Ich denke dieser Zusammenhang ist für die Quantisierung fundamental (abgesehen von den Komplikationen, die ich oben erwähnt habe) und nicht lediglich eine Frage der Zweckmäßigkeit. Genau die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. . Ich denke dieser Zusammenhang ist für die Quantisierung fundamental (abgesehen von den Komplikationen, die ich oben erwähnt habe) und nicht lediglich eine Frage der Zweckmäßigkeit. Genau die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. |
Moment.
Meinst du jetzt mit Einteilchenzuständen solche, die du direkt aus Linearkombinationen von  – ggf. nach Massenrenormierung – ableitest? Also im wesentlichen wieder die Struktur der freien Theorie? – ggf. nach Massenrenormierung – ableitest? Also im wesentlichen wieder die Struktur der freien Theorie?
|
Ich meine mit Einteilchenzustand einen Eigenzustand zum Operator  , wobei , wobei  der exakte Hamiltonoperator ist. Das hat also erstmal nichts mit der freien Theorie zu tun. Solche Eigenzustände erhalte ich auch nicht einfach aus Linearkombinationen der Feldoperatoren, sondern, im Falle eines wechselwirkenden Skalarfeldes, aus den asymptotischen Feldern der exakte Hamiltonoperator ist. Das hat also erstmal nichts mit der freien Theorie zu tun. Solche Eigenzustände erhalte ich auch nicht einfach aus Linearkombinationen der Feldoperatoren, sondern, im Falle eines wechselwirkenden Skalarfeldes, aus den asymptotischen Feldern
|\vec{p}\rangle \equiv |g,m\rangle = -iZ^{-1/2}\lim_{t\to\pm\infty}\int\dd^3 x\left(\int\dd^3 p g(\vec{p})e^{ipx}\right) \overset{\leftrightarrow}{\partial_t}\phi(\vec{x},t)|0\rangle \qquad\text{(1P}))
Der Operator auf der rechten Seite ist also der Erzeuger von  aus dem (nichtperturbativen) Vakuum aus dem (nichtperturbativen) Vakuum 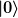 , obwohl , obwohl  ein wechselwirkendes Feld ist. ein wechselwirkendes Feld ist.
Diese Beziehung gilt nur, wenn |0\rangle \neq 0) für irgendein m. Sie erfordert also, daß die Spektralfunktion die Form für irgendein m. Sie erfordert also, daß die Spektralfunktion die Form
\sim Z\delta(p^2 - m^2) + \ldots)
hat. Andernfalls erzeugt  keine Einteilchenzustände und keine Einteilchenzustände und  ist ein Bindungszustand. In diesem Fall muß ist ein Bindungszustand. In diesem Fall muß
\cdots \phi(x_n)|0\rangle\neq 0)
für irgendein Produkt von Feldern gelten, denn Summen (bzw. Reihen) solcher Produkte spannen den gesamten Hilbertraum auf. Dann ergibt sich das erzeugende Feld also in irgendeiner From aus Produkten elementarer Felder, z.B. für n=2 aus
 = \int \dd^4 x f(x)T\left[\phi\left(X+\frac{x}{2}\right)\phi\left(X - \frac{x}{2}\right)\right],)
welches zur Konstruktion von Erzeugern in (1P) eingesetzt werden kann.
In jedem Fall geht die explizite Definition der Erzeuger und Vernichter aus den wechselwirkenden elementaren Feldern deutlich über algebraische Relationen hinaus und erfordert Kenntnisse der Dynamik der Theorie (u.a. der Spektralfunktion ) , und der Zweipunktfunktion , und der Zweipunktfunktion \phi(y))|0\rangle) zur Berechnung der Feldrenormierung Z). zur Berechnung der Feldrenormierung Z).
| Zitat: |
Das entspräche deiner Aussage | Zitat: | | die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. |
Oder meinst du | Zitat: | | die stabilen Impulseigenzustände der QCD – Protonen plus Neutronen und Pionen – die allenfalls durch farbneutrale Produkte von wechselwirkenden Quarkfeldern interpoliert werden. |
Letztere haben zunächst nichts mit dem Fockraum zu tun, der im Zuge der Quantisierung konstruiert wird und in dem die n-Teilchen-Zustände von z.B. asymptotisch freien Quarks und Gluonen leben.
|
Ich sehe da keinen Widerspruch. Ich verlange ja nicht, daß freie Teilchen allein durch elementare Felder erzeugt werden.
| Zitat: |
Wie Mesonen und Baryonen im o.g. Fockraum definiert werden ist bis heute im wesentlichen unbekannt;
|
Das wird vermutlich wegen Haags Theorem auch gar nicht funktionieren. Dies spielt aber keine Rolle, denn der Hilbertraum der exakten QCD muß nichts mit dem Fockraum freier Quarks und Gluonen zu tun haben.
| Zitat: |
und wie direkt ein physikalischer Fockraum inklusive der Erzeuger und Vernichter dieser physikalischen Zustände der Mesonen und Baryonen konstruiert wird, ebenfalls.
|
Die Konstruktion eines Fockraums selbst ist doch trivial. Man benötigt dafür im Prinzip nicht mehr als die bekannten Quantenzahlen der Mesonen und Baryonen. Was nicht trivial ist, ist die Beantwortung der Frage, was der so konstruierte Fockraum mit der Dynamik von wechselwirkenden Quark- und Gluonenfeldern zu tun hat. Dieselbe Frage kannst du auch über den Fockraum freier Quarks stellen. Auch da ist sie nicht trivial. Und die Antworten auf beide Fragen werden vermutlich sehr unterschiedlich sein.
| Zitat: |
Ich wollte an keiner Stelle andeuten, dass ich irgendetwas über eine Fockraumstruktur der Lösungen der QCD aussagen kann; ich wüsste noch nicht mal, ob es eine solche Fockraumstruktur gibt oder überhaupt geben muss (wenn es sie gibt, kann sie nicht unitär äquivalent zum Fockraum der freien Theorie sein).
|
Ja dem stimme ich absolut zu. Das widerspricht doch aber jetzt vollständig deinen Aussagen oben, nach denen die Konstruktion nur die bekannten Vertauschungsrelationen benötigt, und daß sogar die Bindungszustände, in diesem Fockraum liegen. Ich verstehe überhaupt nicht mehr, was du eigentlich behauptest.
| Zitat: |
Und ein | Zitat: | Zusammenhang zwischen den [physikalischen] Einteilchenzuständen [wie Nukleonen] und den Lösungen der Feldgleichung \Phi = 0) ” ” |
ist im Falle der QCD unbekannt, d.h. die Aussage | Zitat: | | dieser Zusammenhang ist für die Quantisierung fundamental |
kann nicht richtig sein, und | Zitat: | | die komplexen Lösungen dieser Gleichung mit positiver Frequenz bilden im wesentlichen den 1-Teilchen-Hilbertraum der zugehörigen Quantentheorie. |
kann sich demnach doch nur auf den Fockraum der freien oder asymptotisch freien Theorie beziehen.
|
Der Begriff Teilchen bezieht sich bei mir auch auf die asymptotischen Zustände. Der Zusammenhang zwischen den in- und out-Feldern, die diese Zustände erzeugen und der Dynamik der elementaren Heisenberg-Felder mag im Falle der QCD (so wie eigentlich im Falle jeder wechselwirkenden QFT in 3+1 Dimensionen) nicht explizit bekannt sein. Das heißt aber noch nicht, daß er nicht von fundamentaler Bedeutung ist.
Aber vielleicht stimmst du mir eher zu, wenn ich sage: er folgt aus recht allgemeinen Eigenschaften quantisierter Felder, von denen man annimmt, daß sie im wesentlichen auch auf die QCD zutreffen. Irgendwelche Aussagen zu freien Protonen und deren S-Matrix werden ja hoffentlich aus der QCD folgen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zitat: | Nach meinem Verständnis folgt eine Fockraumstruktur formal alleine aus den Vertauschungsrelationen der Erzeuger und Vernichter sowie aus der Vollständigkeit des Funktionensystems.
|
Nein, das kann nicht stimmen. Die Fockraumstruktur kann doch nicht unabhängig von der Wechselwirkung sein. Wenn es stimmte, was du sagst, hätten Elektronen und Quarks im wesentlichen dieselben Zustände, denn ihre Vertauschungsrelationen sind eindeutig durch ihren Spin bestimmt, der für beide Teilchen gleich ist. |
Zunächst ist das – bis auf Color und Flavor – für die fermionischen Fockräume der freien Theorien tatsächlich der Fall; die Fockräume sind identisch. Im Falle der QED bleibt diese Struktur bis auf Renormierung im Wesentlichen erhalten, im Falle der QCD ist es komplizierter: man verwendet zwar den Fockraum der freien Theorie zur Quantisierung, allerdings bleibt dieser nur im asymptotisch freien Sektor der Theorie physikalisch relevant; im IR-Sektor der Baryonen und Mesonen ist eine Fockraumstruktur dieser physikalischen Freiheitsgrade unbekannt.
|
Ich habe mir jetzt lange über diese und ähnliche Formulierungen den Kopf zerbrochen und habe den Eindruck, daß hier irgendwas faul ist. Versuchen wir das mal zu klären.
Zunächst verstehe ich unter "QCD" natürlich nicht einfach eine freie Theorie mit SU(3)-Symmetrie. Ich meine schon die echte wechselwirkende Theorie. Was du also "zunächst" mit der freien Theorie machst, ist irrelevant. Das Resultat unterscheidet die QCD-Zustände sehr drastisch von den QED-Zuständen, aber nicht die kanonischen Vertauschungsrelationen der Felder. Und darauf kommt es mir an.
Desweiteren verwendet man m.E. nicht den Fockraum freier Quarks und Gluonen "zur Quantisierung". Das heißt natürlich nicht, daß man ihn für gar nichts verwendet. Man führt ihn ein, um bestimmte QCD-Prozesse auszurechnen, die bei hohen Energien stattfinden. Das ist alles. Er ist aber nicht notwendiger Bestandteil jener quantisierten SU(3)-Eichtheorie, die wir als "QCD" bezeichnen und die wir für alle Phänomene der starken Wechselwirkung verantwortlich machen.
Diese Theorie ist allein durch einen Satz Felder , G_{a\mu\nu}(x)) definiert, die die bekannten Transformationseigenschaften unter der lokalen SU(3)- sowie der Poincaregruppe besitzen. Die Quantentheorie dieser Felder erfordert zusätzlich nur, daß es irgendeinen Hilbertraum H gibt, auf dem sie als Operatoren mit nichtrivialem Definitionsbereich wirken können. Welche Struktur dieser Hilbertraum hat, ist eine komplizierte Frage, die praktisch ungeklärt ist. Sie ist äquivalent zu der Frage welche Eigenschaften die Funktionen definiert, die die bekannten Transformationseigenschaften unter der lokalen SU(3)- sowie der Poincaregruppe besitzen. Die Quantentheorie dieser Felder erfordert zusätzlich nur, daß es irgendeinen Hilbertraum H gibt, auf dem sie als Operatoren mit nichtrivialem Definitionsbereich wirken können. Welche Struktur dieser Hilbertraum hat, ist eine komplizierte Frage, die praktisch ungeklärt ist. Sie ist äquivalent zu der Frage welche Eigenschaften die Funktionen
 = \langle 0|Q_a(x)\cdots Q_b(y)\cdots |0\rangle)
etc. haben und hängt somit offenbar allein von der Dynamik der Felder ab. Sie erfordert an keiner Stelle irgendwelche a-priori-Annahmen über die Existenz von Erzeugern und Vernichtern freier Quarks oder Gluonen. Sie erfordert nicht mal die Annahme, daß H eine Fockraumstruktur besitzt. Obwohl es absolut plausibel ist, daß er Einteilchen- und n-Teilchenzustände für freie Protonen enthält. Ebensowenig erfordert sie aus prinzipiellen Gründen die Entwicklung der Felder nach irgendwelchen Funktionensystemen.
(Die restlichen Punkte sind nun, glaube ich, schon beantwortet, deshalb mach ich hier mal Schluß.) |
|
 |
|
|
