| Autor |
Nachricht |
Patrick
Anmeldungsdatum: 05.07.2006
Beiträge: 417
Wohnort: Nieder-Wöllstadt
|
 Patrick Verfasst am: 13. Jun 2007 15:47 Titel: Lagrange-Gleichung für eine Strömung Patrick Verfasst am: 13. Jun 2007 15:47 Titel: Lagrange-Gleichung für eine Strömung |
 |
|
Ein rechteckiger Fluss mit der Breite b und der Länge l und der Wassertiefe h hat am Anfang eine konstante Strömungsgeschwindigkeit von v0, bis das Wasser zu einer Kugel, die unbewegt im Wasser liegt, mit Radius R gelangt. Es entsteht dann eine Reibungskraft, die sich mit dem Lagrange-Formalismus berechnen lässt. Stellen Sie die Euler-Lagrange-Gleichung und die Dissipationsfunktion (Reibungsfunktion) auf und
errechnen sie die Stokes'sche Reibungskraft an der Kugel:

Wie mache ich das? 
Kann mir jemand dabei helfen? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
|
 |
Patrick
Anmeldungsdatum: 05.07.2006
Beiträge: 417
Wohnort: Nieder-Wöllstadt
|
 Patrick Verfasst am: 13. Jun 2007 19:36 Titel: Patrick Verfasst am: 13. Jun 2007 19:36 Titel: |
 |
|
Dieses kenne ich schon!
Aber es treten beim Öffnen des Dokuments dort Fehler auf!
Man kann aber eine Dissipationsfunktion aufstellen!
Es gilt:

Geht das vielleicht dann? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 17. Jun 2007 20:36 Titel: dermarkus Verfasst am: 17. Jun 2007 20:36 Titel: |
 |
|
Hallo Patrick,
was du da lernen willst, ist ziemlich viel Arbeit. Wenn du dich trotzdem daran wagen willst, kannst du den folgenden Weg versuchen nachzugehen:
-----------------------------
Deine Überlegung, dass das etwas mit Euler-Langrange-Gleichungen zu tun hat, in denen zusätzlich ein Dissipationsterm eingefügt wird, ist vollkommen richtig. In der Kontinuumsmechanik betrachtet man das ganze nicht für Punktteilchen, sondern für kontinuierliche Medien.
http://bibsrv.physik.rwth-aachen.de/Skripte/HTML/Schnakenberg/Thermo99/thbx/node33.html
Damit bekommt man die sogenannte Eulersche Gleichung der Hydrodynamik
http://bibsrv.physik.rwth-aachen.de/Skripte/HTML/Schnakenberg/Thermo99/thbx/node34.html
Berücksichtigt man zusätzlich noch die Zähigkeit des Mediums, gelangt man zur sogenannten Navier-Stokes-Gleichung
http://bibsrv.physik.rwth-aachen.de/Skripte/HTML/Schnakenberg/Thermo99/thbx/node35.html
Diese dient als Ausgangspunkt für die
=========================================
Herleitung der Formel für das Stokes'sche Gesetz
=====================================
[ nach http://aemes.mae.ufl.edu/~uhk/STOKESDRAG.pdf von Dr. Ulrich H. Kurzweg, von mir vom Englischen ins Deutsche übersetzt und etwas ergänzt. Meine Ergänzungen an manchen Stellen zum besseren Verständnis sind mit eckigen Klammern [] gekennzeichnet. Ich habe mich bemüht, die Formeln möglichst gut lesbar zu machen, indem ich die Variablenbezeichnungen so gewählt habe, wie es mir im deutschsprachigen Raum üblich zu sein scheint, und die Formeln in Latex gesetzt habe. ]
In einer bedeutenden Veröffentlichung von 1851 leitete G. Stokes als erster die grundlegende Formel für die mitschleppende Kraft auf eine Kugel mit Radius  her, die sich mit einer Geschwindigkeit her, die sich mit einer Geschwindigkeit 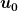 durch eine viskose Flüssigkeit der Dichte durch eine viskose Flüssigkeit der Dichte 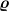 und der Viskosität und der Viskosität  bewegt. Diese Formel lautet bewegt. Diese Formel lautet
 . .
Streng genommen gilt sie nur im Regime laminarer Strömungen, wo die Reynoldszahl  kleiner als 1 ist, deshalb betrifft diese Formel hauptsächlich Kugeln mit sehr kleinem Radius, die entweder von einem Gas oder von einer Flüssigkeit umgeben sind. Die Formel hat in den unterschiedichsten Bereichen Anwendung gefunden, von der Bestimmung der Elementarladung des Elektrons [im Millikan-Versuch] bis zur Vorhersage der Sedimentationsgeschwindigkeit in Suspensionen. In der Biologie begegnet man ihr bei der Untersuchung der Ablagerungsraten von Blutzellen in zentrifugalen Feldern und bei der Bestimmung der Rate, mit der kleine Verunreinigungen in der Lunge abgelagert werden. kleiner als 1 ist, deshalb betrifft diese Formel hauptsächlich Kugeln mit sehr kleinem Radius, die entweder von einem Gas oder von einer Flüssigkeit umgeben sind. Die Formel hat in den unterschiedichsten Bereichen Anwendung gefunden, von der Bestimmung der Elementarladung des Elektrons [im Millikan-Versuch] bis zur Vorhersage der Sedimentationsgeschwindigkeit in Suspensionen. In der Biologie begegnet man ihr bei der Untersuchung der Ablagerungsraten von Blutzellen in zentrifugalen Feldern und bei der Bestimmung der Rate, mit der kleine Verunreinigungen in der Lunge abgelagert werden.
Die meisten einführenden Lehrbücher (und auch viele weitergehenden Bücher über die Physik der Flüssigkeiten) bringen keine volle Herleitung des Stokes'schen Gesetzes, hauptsächlich weil man dazu ziemlich viel Mathematik braucht. Wir helfen hier, dieser Situation Abhilfe zu schaffen, indem wir eine vollständige Herleitung vorstellen.
Zu Beginn führen wir ein Koordinatensystem in Kugelkoordinaten ein und platzieren die Kugel mit Radius  in der Mitte. Die Strömung des viskosen und inkompressiblen Mediums um diese Kugel wird aufgrund von Symmetrieüberlegungen nur Geschwindigkeitskomponenten haben, die von der radialen Koordinate in der Mitte. Die Strömung des viskosen und inkompressiblen Mediums um diese Kugel wird aufgrund von Symmetrieüberlegungen nur Geschwindigkeitskomponenten haben, die von der radialen Koordinate  und vom Polarwinkel und vom Polarwinkel 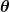 abhängen. Weil die Divergenz dieses Geschwindigkeitsfeldes Null ist, kann man die Strömungsfunktion abhängen. Weil die Divergenz dieses Geschwindigkeitsfeldes Null ist, kann man die Strömungsfunktion ) einführen, die definiert ist durch einführen, die definiert ist durch
 und und  . .
[Die Bewegungsgleichung für Flüssigkeiten und Gase, die aus der Impulserhaltung folgt, ist die sogenannte Navier-Stokes-Gleichung
 . .
Die von uns betrachtete laminare Strömung ist zeitunabhängig ) und Effekte der Schwerkraft auf das strömende Medium werden vernachlässigt und Effekte der Schwerkraft auf das strömende Medium werden vernachlässigt ) . .
Damit erhalten wir die Bewegungsgleichung
 ] ]
Für eine inkompressible Flüssigkeit mit Divergenz Null ist ) , damit kann man die Komponenten dieser Bewegungsgleichung nach ein bisschen Umformen schreiben als , damit kann man die Komponenten dieser Bewegungsgleichung nach ein bisschen Umformen schreiben als
}{\partial \theta} ) und und }{\partial r}) , ,
dabei ist 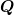 ein Differentialoperator, der definiert ist als ein Differentialoperator, der definiert ist als
) . .
Durch Eliminieren von 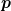 aus diesen beiden Gleichungen erhält man die partielle Differentialgleichung vierter Ordnung aus diesen beiden Gleichungen erhält man die partielle Differentialgleichung vierter Ordnung

Mit der Substitution
 \sin^2 \theta)
kann man diese Gleichung auf eine gewöhnliche Differentialgleichung vierter Ordnung vom Eulerschen Typ reduzieren, nämlich:
 . .
Diese Gleichung kann man prima mit der Substitution  lösen, das führt zu der Lösung lösen, das führt zu der Lösung
 . .
Die vier Konstanten  , , 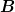 , , 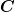 und und 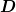 können wir aus der Tatsache bestimmen, dass beide Geschwindigkeitskomponenten an der Oberfläche der Kugel bei können wir aus der Tatsache bestimmen, dass beide Geschwindigkeitskomponenten an der Oberfläche der Kugel bei  verschwinden [denn die Flüssigkeit haftet ja an der Kugeloberfläche] und dass verschwinden [denn die Flüssigkeit haftet ja an der Kugeloberfläche] und dass  für große für große  gegen gegen  geht [denn weit weg von der Kugel hat man ja einfach eine parallele Strömung mit Geschwindigkeit geht [denn weit weg von der Kugel hat man ja einfach eine parallele Strömung mit Geschwindigkeit 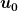 ]. Das führt zu der Stokes'schen Strömungsfunktion ]. Das führt zu der Stokes'schen Strömungsfunktion
 \sin^2 \theta) . .
Aus diesem letzten Ergebnis, und unter Verwendung der oben angegebenen Definitionen für die Geschwindigkeitskomponenten und den radialen Druckgradienten erhält man auch die Beziehungen
 \cos \theta) , ,
 \sin \theta)
und
 . .
Die Reibungskraft kann nun berechnet werden, indem man die Scherspannung [tangentiale Kraft pro Fläche] und die Normalspannung [senkrechte Kraft pro Fläche] über die gesamte Oberfläche der Kugel integriert. In dieser Rechnung ist 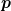 die Normalspannung, und die Scherspannung ist die Normalspannung, und die Scherspannung ist
 + \frac{1}{r} \frac{\partial v_r}{\partial \theta} \right]) . .
Führt man die Integration von  bis bis 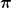 für die durch den Druck verursachte Mitschleppkraft durch, dann erhält man eine resultierende Kraft in z-Richtung [also in Richtung von für die durch den Druck verursachte Mitschleppkraft durch, dann erhält man eine resultierende Kraft in z-Richtung [also in Richtung von  ] von ] von
 . .
Und die Kraft in z-Richtung durch viskose Scherspannung ergibt sich als
 . .
Wenn wir diese beiden Kräfte zusammenzählen, gelangen wir zu dem berühmten Stokes'schen Gesetz, das von ihm vor 150 Jahren hergeletet wurde! Man beachte, dass hier zwei Drittel der Kraft auf die Kugel durch viskose Scherkräfte und nur ein Drittel durch Druckkräfte verursacht werden. [Der Effekt durch die viskosen Scherkräfte, mit denen das viskose Medium die Kugel tangential mitzieht, ist hier also doppelt so groß wie der Effekt durch die Druckkräfte, mit denen die Strömung die Kugel vor sich her drückt!]
============================================= |
|
 |
|
|
















