| Autor |
Nachricht |
PcIv
Anmeldungsdatum: 20.02.2015
Beiträge: 74
|
 PcIv Verfasst am: 20. März 2015 18:09 Titel: Extremwert bei unstetiger differenzierbarer Funktion |
 |
|
Hallo!
Ich habe diese Funktion gegeben und die einfache Frage hat sie Extrema?
Die Unstetigkeit verwirrt mich und ich bin mit den mathematischen Begrifflichkeiten nicht vertraut genug: Liegt ein Extremwert bei x=0 vor, obwohl eine Unstetigkeit der Ableitung vorliegt? Theoretisch muss ich um einen Extremwert zu ermitteln ableiten und die Ableitung null setzten... Wenn ich das mache erhalte ich aber nur ln(0) und komme nicht weiter. Danach hätte die Funktion also kein Extremwert. Ist der Punkt demnach ein unstetiges Minimum, aber kein Extremwert? Oder ist das Ableiten und null setzten kein Patentrezept, sondern nur bei stetig differenzierbaren Funktionen gültig?
Beste Grüße und vielen Dank!
Pascal
|
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8584
|
| jh8979 Verfasst am: 20. März 2015 18:19 Titel: |
|
|
|
Extremum ist üblicherweise definiert als lokales und/oder globales Maximum/Minimum. Dieser Fall liegt hier vor in x=0. Da die Funktion in diesem Punkt aber nicht differenzierter ist, kann man dieses Extremum nicht mit f'(x)=0 finden.
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3405
|
| ML Verfasst am: 20. März 2015 18:52 Titel: Re: Extremwert bei unstetiger differenzierbarer Funktion |
|
|
Hallo,
| PcIv hat Folgendes geschrieben: |
Ich habe diese Funktion gegeben und die einfache Frage hat sie Extrema?
|
Ja, bei x=0 liegt ein Minimum mit dem Funktionswert 2^0=1 vor.
| Zitat: |
Die Unstetigkeit verwirrt mich und ich bin mit den mathematischen Begrifflichkeiten nicht vertraut genug: Liegt ein Extremwert bei x=0 vor, obwohl eine Unstetigkeit der Ableitung vorliegt?
|
Ja. Aber es liegt nicht nur eine "Unstetigkeit der Ableitung" vor, sondern die Ableitung ist an der Stelle x=0 nicht definiert. Es gibt allenfalls eine linksseitige und eine rechtsseitige Ableitung.
| Zitat: |
Theoretisch muss ich um einen Extremwert zu ermitteln ableiten und die Ableitung null setzten...
|
Nein. Das Verfahren mit der Ableitung funktioniert nur, wenn die Funktion an der Stelle differenzierbar ist. Das ist sie aber hier nicht.
| Zitat: |
Ist der Punkt demnach ein unstetiges Minimum, aber kein Extremwert?
|
Die Funktion ist an der Stelle x=0 stetig und es liegt ein ganz normales Minumum (das ist ein Extremwert) vor. Das ist ganz analog wie bei der Betragsfunktion |x|. An x=0 liegt ganz selbstverständlich ein Minimum vor, obwohl |x| an x=0 nicht differenzierbar ist.
| Zitat: |
Oder ist das Ableiten und null setzten kein Patentrezept, sondern nur bei stetig differenzierbaren Funktionen gültig?
|
Es ist kein Allheilmittel, sondern funktioniert nur, wenn die Funktionen, mit denen Du arbeitest, auch definiert sind (insbesondere die Ableitung). Wenn die Funktion stetig differenzierbar ist, bist Du auf der sicheren Seite. Wenn die Funktion nur differenzierbar ist, musst Du auf einen Vorzeichenwechsel der Ableitung an der betreffenden Stelle achten.
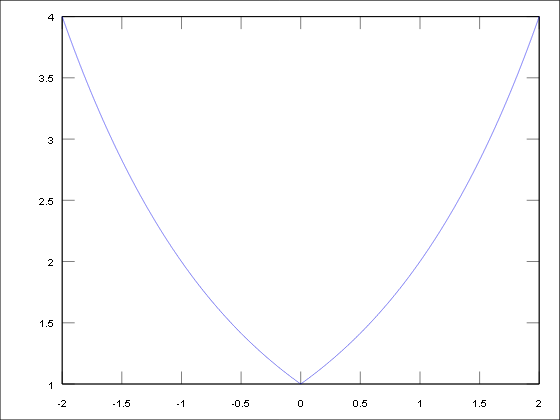
Schauen wir uns die Funktion mal an.
 = 2^{\sqrt{x^2}} = 2^{|x|} = \mathrm{e}^{|x| \cdot \ln(2)} )
Die Funktion ist offenbar überall differenzierbar außer an x=0. Es gilt:
 = \lim\limits_{x \to 0, x>0} \left( \ln(2) \cdot \mathrm{e}^{x \cdot ln(2)} \right) = \ln(2) )
 = \lim\limits_{x \to 0, x<0} \left( -\ln(2) \cdot \mathrm{e}^{-x \cdot ln(2)} \right) = -\ln(2) )
Jetzt schauen wir uns das ganze mal mit Verstand an:
Für x<0 fällt die Funktion; An x = 0 ist sie stetig und für x>0 steigt sie wieder. An x=0 liegt also ein Minimum vor.
Viele Grüße
Michael
| Beschreibung: |
|
| Dateigröße: |
11.72 KB |
| Angeschaut: |
1881 mal |
|
|
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 21. März 2015 01:43 Titel: |
|
|
Mit den Nullstellen der Ableitung findet man das Extremum nicht, wie schon zweimal gesagt wurde. Allerdings ist es in solchen Fällen hilfreich, monotone Transformationen zu betrachten. In diesem Fall braucht das nicht weiter erläutert werden, weil es offensichtlich ist: der Exponent ist minimal, daher auch die ganze Funktion. Ein oft verwendeter Trick ist aber z.B. auch, dass man die Extreme des Logarithmus einer Funktion sucht (z.B. in der statistischen Physik bei Untersuchungen zur Entropie oder bei der Herleitung von Maximum-Likelihood-Schätzern z.B. für die Standardabweichung [sollte man mal gesehen haben, finde ich]).
Da offenbar Unklarheit über den Begriff des Minimums herrscht, kann wohl eine Definition nichts schaden:
Eine Funktion f(x) hat ein lokales Minimum bei x0, falls es eine Umgebung ) gibt, sodass für alle x in U gilt: >f(x_0)) .
Eine Funktion ) heißt streng monoton wachsend, falls aus y>x stets g(y)>g(x) folgt.
Damit ist klar: Hat f(x) ein lokales Minimum bei x0, so gibt es also eine Umgebung U, sodass für alle xin U gilt:  > f(x_0)) . Ist g(x) streng monoton wachsend, so folgt daraus ) > g(f(x_0))) . Das heißt, definitionsgemäß hat dann auch g(f(x)) bei x0 ein lokales Minimum. Die Umkehrung ist auch richtig, weil streng monotone Funktionen immer invertierbar sind und die Inversen dann auch streng monoton sind.
Also konkret ist zum Beispiel die Funktion  = \log_2 x) streng monoton wachsend, daher kann man nach dem Minimum von (x) = \sqrt{x^2} = \vert x \vert ) suchen. Diese wiederum nimmt nur Werte >= 0 an und für x>=0 ist  = x^2) eine streng monoton wachsende Funktion, also sucht man nach dem Minimum von (x) = \vert x \vert^2 = x^2) und das findet man ganz klassisch.
PS: Differenzierbare Funktionen sind meistens auch stetig differenzirbar. Ich kenne nur ein pathologisches Gegenbeispiel: http://upload.wikimedia.org/wikipedia/commons/c/c4/N_stetig_diffb_svg.svg
|
|
|
PcIv
Anmeldungsdatum: 20.02.2015
Beiträge: 74
|
| PcIv Verfasst am: 22. März 2015 16:05 Titel: |
|
|
|
Vielen, vielen Dank für die ausführlichen Antworten. Mir ist einiges klarer geworden.
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
