| Autor |
Nachricht |
PhysikGnom
Gast
|
 PhysikGnom Verfasst am: 04. Nov 2014 00:48 Titel: Lie Gruppen PhysikGnom Verfasst am: 04. Nov 2014 00:48 Titel: Lie Gruppen |
 |
|
Hallo Physiklinge, ich lerne grade etwas über Lie Gruppe und Lie Algebra um die Eichtheorie über Prinzipalbündel zu verstehen, aber ich habe ein paar konzeptuelle Problem, ich fange einfach mal an
Seien  und und 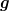 Elemente der Lie Gruppe Elemente der Lie Gruppe 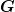 , die Linkstranslation , die Linkstranslation  von von 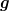 durch durch  ist definiert durch : ist definiert durch : 
welches eine Abbildung induziert  . Sei . Sei 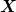 ein Vektorfeld der Lie Gruppe ein Vektorfeld der Lie Gruppe 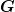 . . 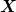 ist ein links invariantes vektorfeld wenn ist ein links invariantes vektorfeld wenn  . Ein Vektor . Ein Vektor  definiert ein links invariantes Vektorfeld definiert ein links invariantes Vektorfeld  durch durch 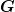 durch: durch:  , , 
Der Autor des Buches gibt nun ein Beispiel von einem links-invarianten Vektorfeld von ) : :
Seien }) und und }) Elemente von Elemente von ) wo wo  das Einselement ist. Die linkstranslation ist: das Einselement ist. Die linkstranslation ist:
x^{kj}(g))
Nun bei dem Vektorfeld  wo wo  die Einträge von die Einträge von 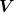 sind. Das linksinvariante Vektorfeld generiert von sind. Das linksinvariante Vektorfeld generiert von 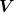 ist: ist:
x^{lm}(e) \frac{\partial}{x^{km}}|_{g}= \Sigma V^{ij}x^{kl}(g) \delta^{l}_{i} \delta^{m}_{j} \frac{\partial}{\partial x^{km}}|_{g}= \Sigma x^{ki}(g)V^{ij} \frac{\partial}{\partial x^{kj}}|_{g}= \Sigma (gV)^{kj} \frac{\partial}{\partial x^{kj}}|_g)
Hier ist  die übliche Matrizenmultiplikation. die übliche Matrizenmultiplikation.
Was bedeutet es wenn man einen Tangentialvektor an dem Einselement einer Lie Gruppe hat? Was bedeutet das anschaulich? Vielleicht hilft diese Aufgabe ein wenig dabei:
Sei
=\begin{pmatrix} cos s & -sin s & 0 \\ sin s & cos s & 0 \\ 0 & 0 & 1 \end{pmatrix})
eine Kurve in ) . Berechne den Tangentialvektor an . Berechne den Tangentialvektor an  . .
Und warum wird überhaupt ein linksinvariantes Vektorfeld induziert? Und was ist überhaupt ein links-invariantes Vektorfeld anschaulich? Und was bedeutet es wenn ein Vektor ( )mehrere Indizes hat? )mehrere Indizes hat?
Kann mir jemand das Beispiel erklären? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8584
|
 jh8979 Verfasst am: 04. Nov 2014 01:33 Titel: Re: Lie Gruppen jh8979 Verfasst am: 04. Nov 2014 01:33 Titel: Re: Lie Gruppen |
 |
|
1. Das Summenzeichen ohne Summationsindex, macht die Formeln noch schwerer lesbar als ohnehin schon...
| PhysikGnom hat Folgendes geschrieben: |
Was bedeutet es wenn man einen Tangentialvektor an dem Einselement einer Lie Gruppe hat? Was bedeutet das anschaulich?
|
Siehe Bild hier:
http://de.wikipedia.org/w/index.php?title=Tangentialraum&redirect=no
Wenn Dir das nicht klar ist, siehe auch hier:
http://de.wikipedia.org/w/index.php?title=Tangentialraum&redirect=no#Tangentialvektoren_als_Richtungsableitungen
| Zitat: |
Und warum wird überhaupt ein linksinvariantes Vektorfeld induziert? Und was ist überhaupt ein links-invariantes Vektorfeld anschaulich?
|
Es wird offensichtlich, sprich: es ergibt sich eine natürliche Definition eines linksinvarianten Vertorfeldes aus dem was vorher definiert wurde. "Links-invariant" heisst, dass das Vertrottelt links-invariant unter ist... wie der Name sagt, vllt hilft da diese Seite etwas weiter:
http://theory.gsi.de/~vanhees/faq/relativity/node120.html
| Zitat: |
Und was bedeutet es wenn ein Vektor ( )mehrere Indizes hat? )mehrere Indizes hat?
|
Der Vekotrraum der nxn Matrixen hat n^2 Basis-Vektoren (die jeweils Matrizen sind). Da ist es einfacher die Koordinaten bezügliche dieser Basis mit zwei Indizes, die von 1 bis n laufen, zu nummerieren, als mit einem Index, der von 1 bis n^2 läuft.
PS: Mathematik ist schoen und gut ... aber man sollte das nicht mit Physik verwechseln ... (nur so als Erinnerung) ... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18188
|
 TomS Verfasst am: 04. Nov 2014 01:42 Titel: TomS Verfasst am: 04. Nov 2014 01:42 Titel: |
 |
|
Vektoren, die mittels Ableitungen am Eins-Element einer Liegruppe definiert werden, bilden die zugehörige Lie-Algebra. Umgekehrt kann die Komponente der Liegruppe, die das Eins-Element enthält, durch die Exponentialfunktion der Liealgebra definiert werden.
Die Vektoren sind Elemente einer Algebra, also ist neben der Addition sowie der Multiplikation mit einer komplexen Zahl noch die Multiplikation innerhalb der Algebra definiert. Diese Vektoren können demnach keine n-Tupel aus komplexen Zahlen sein.
Wenn die Gruppenelemente als Matrizen dargestellt werden (was nicht zwingend so sein muss), dann sind natürlich die Elemente der Liealgebra und insbs. die Basisvektoren ebenfalls Matrizen.
Im Falle der SU(2) ist die zugehörige Liealgebra die su(2), die gerade durch die drei Spinmatrizen (Paulimatrizen * 1/2) aufgespannt wird. Die Spinmatrizen bilden eine Basis, d.h. jedes Element der Algebra kann durch eine geeignete Linearkombination der Basisvektoren dargestellt werden.
Wir haben




d.h. die Umgebung des Einselementes g=1 der SU(2) entspricht der Umgebung des Nullelementes X=0 der su(2). Die Generatoren t folgen dann durch Differentation nach den Parametern x in der Umgebung von x=0.

In meiner Konvention sind die Generatoren hermitesch. Mathematiker schreiben das "i" manchmal nicht explizit, dann sind die Generatoren anti-hermitesch.
Physikalisch sind die t's die Spinoperatoren. Die Gruppenelemente g sind Drehungen im Spinraum, d.h. Drehungen der Spinvektoren (= der Zustände, hier nicht geschrieben) bzw. Drehungen der Basis t. Die Drehwinkel entsprechen den Parametern x.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
PhysikGnom
Gast
|
 PhysikGnom Verfasst am: 04. Nov 2014 17:17 Titel: PhysikGnom Verfasst am: 04. Nov 2014 17:17 Titel: |
 |
|
Hallo, danke für die Antworten.
Also ich kennen natürlich die Tangentialräume usw. Wenn man eine Riemann Mannigfaltigkeit hat kann man sich diese ja oft einfach im R^3 vorstellen mit dazugehörigem Tangentialraum. Aber wie sieht das bei Lie Gruppen aus? Wenn ich an Gruppen denke hab ich meistens endliche Permutationsgruppen im Kopf und da macht es irgendwie keinen Sinn von einem Tangentialvektor am Einselement oder Tangentialraum zu reden.
Aber ich will es kurz zusammenfassen:
Eine Lie Gruppe hat einen Tangentialraum (der ein Vektorraum ist) (wie jede Mannigfaltigkeit).
Der Tangentialraum ist der Raum der Lie Algebra der Gruppe.
Wenn ich zwei linksinvariante Vektorfelder im Tangentialraum definiere kann ich eine Lie Klammer konstruieren die eine Lie Algebra definiert. Und wenn ich diese Vektorfelder linksmultipliziere mit einem Gruppenelement dann kann ich die Vektorfelder von einem in dem anderen Tangentialraum verschieben? Ist das dann schon Paralleltransport durch einen Zusammenhang? Und wieso braucht man das Einselement um einen Tangentialvektor auf der Mannigfaltigkeit zu verschieben? Hat das was mit koset Multiplikation zu tun? Und wie geht das mit der Linearkombination von Vektorfeldern um eine Lie Klammer darzustellen?
Könnte vielleicht jemand die Aufgabe die ich oben geschrieben habe erklären, bzw. kurz anschaulich ausrechnen, oder sagen was man da machen muss. (Die Werbebanner sind übrigens sehr lustig "Trust in German Sicherheit). |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8584
|
 jh8979 Verfasst am: 04. Nov 2014 17:25 Titel: Re: Lie Gruppen jh8979 Verfasst am: 04. Nov 2014 17:25 Titel: Re: Lie Gruppen |
 |
|
| PhysikGnom hat Folgendes geschrieben: |
Sei
=\begin{pmatrix} cos s & -sin s & 0 \\ sin s & cos s & 0 \\ 0 & 0 & 1 \end{pmatrix})
eine Kurve in ) . Berechne den Tangentialvektor an . Berechne den Tangentialvektor an  . . |
Ich nehme mal an, dass I_3 die Einheitsmatrix sein soll.
Es gilt offensichtlich c(0)=I_3 und somit
|_{s=0}=\begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} = J_z)
wobei J_z einfach der Generator der Rotationen um die z-Achse ist. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18188
|
 TomS Verfasst am: 04. Nov 2014 17:35 Titel: TomS Verfasst am: 04. Nov 2014 17:35 Titel: |
 |
|
| PhysikGnom hat Folgendes geschrieben: | | Wenn ich an Gruppen denke hab ich meistens endliche Permutationsgruppen im Kopf und da macht es irgendwie keinen Sinn von einem Tangentialvektor am Einselement oder Tangentialraum zu reden. |
Aber das ist bei Liegruppen nunmal anders. Diese sind topologische Mannigfaltigkeiten; die o.g. Parametersdarstellung von g mittels x ist sogar analytisch und glatt in x.
| PhysikGnom hat Folgendes geschrieben: | | Eine Lie Gruppe hat einen Tangentialraum (der ein Vektorraum ist) (wie jede Mannigfaltigkeit). |
ja
| PhysikGnom hat Folgendes geschrieben: | | Der Tangentialraum ist der Raum der Lie Algebra der Gruppe. |
ja
| PhysikGnom hat Folgendes geschrieben: | | Wenn ich zwei linksinvariante Vektorfelder im Tangentialraum definiere kann ich eine Lie Klammer konstruieren die eine Lie Algebra definiert. |
ja, so rum kannst du's auch machen
| PhysikGnom hat Folgendes geschrieben: | | Und wenn ich diese Vektorfelder linksmultipliziere mit einem Gruppenelement dann kann ich die Vektorfelder von einem in dem anderen Tangentialraum verschieben? Ist das dann schon Paralleltransport durch einen Zusammenhang? |
die Linksmultiplikation ist doch noch keine Lieableitung, sondern nur eine lokale Koordinatentransformation innerhalb eines Tangentialraumes; der Paralleltransport, d.h. die kovariante Ableitung wirkt zwischen benachbarten Tangentialräumen (im Tangentialraumbündel)
| PhysikGnom hat Folgendes geschrieben: | | Und wieso braucht man das Einselement um einen Tangentialvektor auf der Mannigfaltigkeit zu verschieben? |
braucht man i.A. nicht; aber im Falle der Liegruppe besteht dieser spezielle Zusammenhang; in diesem speziellen Fall ist die Mannigfaltigkeit eben zusätzlich eione Gruppe.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
PhysikGnom
Gast
|
 PhysikGnom Verfasst am: 04. Nov 2014 17:42 Titel: PhysikGnom Verfasst am: 04. Nov 2014 17:42 Titel: |
 |
|
|
Ah achso funktioniert das. Danke jh8979. Und wie würde jetzt das linksinvariante Vektorfeld aussehen?? |
|
 |
scka
Gast
|
 scka Verfasst am: 04. Nov 2014 17:43 Titel: scka Verfasst am: 04. Nov 2014 17:43 Titel: |
 |
|
An Permutationsgruppen soll man hier natürlich nicht denken. Die sind diskret, Liegruppen sind aber immer kontinuierlich.
Alldieweil stimmt die Behauptung
"Diese Vektoren können demnach keine n-Tupel aus komplexen Zahlen sein "
so nicht, ein einfaches Gegenbeispiel ist bereits das Kreuzprodukt.
Die Lie-Klammer ist auf Wikipedia recht ausführlch erklärt. |
|
 |
PhysikGnom
Gast
|
 PhysikGnom Verfasst am: 04. Nov 2014 17:43 Titel: PhysikGnom Verfasst am: 04. Nov 2014 17:43 Titel: |
 |
|
|
Oh, Danke Tom, also wie würde im falle der gelöst Aufgaben von jh8979, das linksinvariante Vektorfeld aussehen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18188
|
 TomS Verfasst am: 04. Nov 2014 17:52 Titel: TomS Verfasst am: 04. Nov 2014 17:52 Titel: |
 |
|
| scka hat Folgendes geschrieben: | Alldieweil stimmt die Behauptung
"Diese Vektoren können demnach keine n-Tupel aus komplexen Zahlen sein "
so nicht, ein einfaches Gegenbeispiel ist bereits das Kreuzprodukt. |
OK, nettes (einziges?) Gegenbeispiel
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8584
|
 jh8979 Verfasst am: 04. Nov 2014 18:02 Titel: jh8979 Verfasst am: 04. Nov 2014 18:02 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | scka hat Folgendes geschrieben: | Alldieweil stimmt die Behauptung
"Diese Vektoren können demnach keine n-Tupel aus komplexen Zahlen sein "
so nicht, ein einfaches Gegenbeispiel ist bereits das Kreuzprodukt. |
OK, nettes (einziges?) Gegenbeispiel |
Und auch nur für n=3... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18188
|
 TomS Verfasst am: 04. Nov 2014 18:05 Titel: TomS Verfasst am: 04. Nov 2014 18:05 Titel: |
 |
|
irgendwas war mit n=7
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
PhysikGnom
Gast
|
 PhysikGnom Verfasst am: 04. Nov 2014 18:19 Titel: PhysikGnom Verfasst am: 04. Nov 2014 18:19 Titel: |
 |
|
|
Ein zu einem Bivektor dualen Vektor gibt's nur in n=3 und n=7 soweit ich weiß. (knowledge dropping) |
|
 |
scka
Gast
|
 scka Verfasst am: 04. Nov 2014 18:33 Titel: scka Verfasst am: 04. Nov 2014 18:33 Titel: |
 |
|
Ein Produkt im Vektorraum wird über Strukturkonstanten eingeführt:
wikipedia: Strukturkonstante
Wenn n dabei nur bestimmte Werte annehmen darf, würde das erwähnt werden, glaube ich.
Ich schreibe dort also für jeden Vektor aus V seine Linearfaktoren bzgl der xi in eine Spalte und bin fertig. |
|
 |
scka
Gast
|
 scka Verfasst am: 04. Nov 2014 19:24 Titel: scka Verfasst am: 04. Nov 2014 19:24 Titel: |
 |
|
Kleiner Nachtrag:
Für R^3 mit Kreuzprodukt sind die Strukturkonstanten gegeben durch den epsilontensor.
Führt man das oben beschriebene damit aus, landet man bei der bekannten Formel mit den gekreuzten Linien zwischen den Spaltenvektoren.
Das ist halt das gebräuchlichste Produkt in einem Vektorraum, was aber nicht heisst dass es "natürlicher" oder naheliegender als andere Produkte in Vektorräumen wäre. |
|
 |
PhysikGnom
Gast
|
 PhysikGnom Verfasst am: 04. Nov 2014 20:09 Titel: PhysikGnom Verfasst am: 04. Nov 2014 20:09 Titel: |
 |
|
In der geometrischen Algebra wo man das geometrische Produkt benutzt  für Vektoren für Vektoren  und und 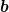 kann man das Kreuzprodukt auch über den Pseudoskalar definieren als kann man das Kreuzprodukt auch über den Pseudoskalar definieren als ) für für 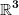 ist ist  , z.B. , z.B. = -e_{1}e_{2}e_{3}e_{1}e_{2}=-e_{1}e_{2}e_{1}e_{2}e_{3}=e_{1}e_{1}e_{2}e_{2}e_{3}=e_{3})
Ok aber zurück zur Eichtheorie. Also allgemein bekommt man ja den Zusammenhang von einer 1-form  die durch die durch  gegeben ist, wobei gegeben ist, wobei  gegeben ist, und die Basis gegeben ist, und die Basis  , ,  erfüllt (wo kommt diese Lie Algebra her?). Nun kann man ja den Tangentialraum der Prinzipalbündel (die ja eine Lie Gruppe ist) zerlegen in: erfüllt (wo kommt diese Lie Algebra her?). Nun kann man ja den Tangentialraum der Prinzipalbündel (die ja eine Lie Gruppe ist) zerlegen in:
=V(P) \bigoplus H(P))
Nun steht im Text das  die Basis ist, ist das jetzt aber die Basis von komplett die Basis ist, ist das jetzt aber die Basis von komplett ) oder nur vom horizontalen Unterraum oder nur vom horizontalen Unterraum ) ? Weil später steht : ? Weil später steht :  and and  being the basis vectors for being the basis vectors for ) and and ) respectively. respectively.  Und warum muss die Kondition Und warum muss die Kondition  gelten für gelten für  wenn wenn ) ist um ist um  zu bestimmen? zu bestimmen?  |
|
 |
PhysikGnom
Gast
|
 PhysikGnom Verfasst am: 04. Nov 2014 20:13 Titel: PhysikGnom Verfasst am: 04. Nov 2014 20:13 Titel: |
 |
|
Es heisst natürlich   |
|
 |
PhysikGnom

Anmeldungsdatum: 04.11.2014
Beiträge: 77
|
 PhysikGnom Verfasst am: 05. Nov 2014 19:49 Titel: PhysikGnom Verfasst am: 05. Nov 2014 19:49 Titel: |
 |
|
Hallo, kann wenigstens jemand zum zweiten Teil meiner Frage was sagen?  |
|
 |
scka
Gast
|
 scka Verfasst am: 05. Nov 2014 20:30 Titel: scka Verfasst am: 05. Nov 2014 20:30 Titel: |
 |
|
Zum 2ten Teil Deiner Frage:
Soweit ich mich erinnere, sind das die 2 äquivalenten Möglichkeiten, einen Zusammenhang festzulegen.
Entweder wird für jeden Punkt im Prinzipalbündel der Horizontale Unterraum sozusagen von Hand festgelegt über die Koeffizienten C (das was im Text steht muss die Basis von H(P) sein).
Oder man hat eine 1Form omega auf P, dann ist ein Vektor aus T(P) dann horizontal, wenn er eingesetzt in omega 0 gibt. |
|
 |
PhysikGnom

Anmeldungsdatum: 04.11.2014
Beiträge: 77
|
 PhysikGnom Verfasst am: 05. Nov 2014 22:09 Titel: PhysikGnom Verfasst am: 05. Nov 2014 22:09 Titel: |
 |
|
Hallo scka, also ich hab das so verstanden das der ) und und ) nicht orthogonal sein müssen z.B. wie bei nicht orthogonal sein müssen z.B. wie bei  \bigoplus (x,ax)) wo wo ) den Vektorraum den Vektorraum  für ein fixes für ein fixes  aufspannt (für aufspannt (für 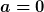 wäre die Basen orthogonal). Stimmt das? wäre die Basen orthogonal). Stimmt das? |
|
 |
scka
Gast
|
 scka Verfasst am: 06. Nov 2014 12:17 Titel: scka Verfasst am: 06. Nov 2014 12:17 Titel: |
 |
|
Ja, so kann man sichs vorstellen.
Trotzdem muss man dabei mit dem Wort „orthogonal“ aufpassen weil man in einem Prinzipalbündel i.A. kein Skalarprodukt oder Metrik hat. Ein Zusammenhang gibt einem die Möglichkeit, ohne ein solches festzulegen was in P „orthogonal zu V(P)“ bedeuten soll. |
|
 |
PhysikGnom

Anmeldungsdatum: 04.11.2014
Beiträge: 77
|
 PhysikGnom Verfasst am: 06. Nov 2014 22:49 Titel: PhysikGnom Verfasst am: 06. Nov 2014 22:49 Titel: |
 |
|
Ok danke. Ich will die Herleitung vom Eichpotential verstehen und da fehlen noch ein paar Bausteine.
Also man braucht ja eine Zusammenhangs-eins-form 
Und die muss erfüllen :
I =A, A \in \mathfrak{g})
( ist das fundamental Vektorfeld) ist das fundamental Vektorfeld)
Was wohl bedeutet das ich als Input in die eins-form das fundamental Vektorfeld habe und der output die Lie Algebra die isomorph zum Tangentialraum des Prinzipalbündels der Lie Grupp ist herausbekomme.
II 
Was in worten bedeutet das die rechtstranslation der eins-form im kotangentialraum durch das Element 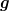 der Lie Gruppe gleich der adjungierten Abbildung von dem inversen Element an der Lie Gruppe gleich der adjungierten Abbildung von dem inversen Element an  sein muss. sein muss.
Was bedeutet jetzt Ad ? Ich kenne die normale adjungiert Abbildung Ad ? Ich kenne die normale adjungiert Abbildung Ad durch durch  . .
Aber wie sieht dann Ad aus? aus?
Hier ein Beispiel für  : :
= \omega_{ug}(R_{g*}X)=g^{-1}\omega_{u}(X)g)
Was bedeutet jetzt der letzte Term? Und wie teilt diese eins-form den Tangentialraum in horizontal und vertikal??
Später jetzt man dann den =0}) . .
LG |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18188
|
 TomS Verfasst am: 06. Nov 2014 23:10 Titel: TomS Verfasst am: 06. Nov 2014 23:10 Titel: |
 |
|
Ich denke bei "Ad" handelt es sich um die adjungierte Darstellung der Gruppe. In diesem Fall ist der Vektorraum, auf dem die Darstellung der Gruppe operiert, identisch mit der Algebra.
Üblicherweise hat man ja eine Darstellung der Form

wobei v z.b. ein Vektor im R^n oder ein Spinor ist.
Im Falle der adjungieren Darstellung ist jedoch

wobei X ein Element der Algebra selbst ist.
Anmerkung: Man erhält aus dem Kommutator der Generatoren

die Strukturkonstanten f. Diese definieren selbst die Generatoren in der adjungierten Darstellung, d.h.
_{bc})
Anmerkung 2: da dies ein Physikforum ist, sei die Anmerkung erlaubt, dass der Feldstärketensor F einer Eichtheorie in einem Faserbündel über der adjungierten Darstellung der Liealgebra "lebt", während die Materiefelder üblicherweise Spinoren in der Fundamentaldarstellung sind.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
PhysikGnom

Anmeldungsdatum: 04.11.2014
Beiträge: 77
|
 PhysikGnom Verfasst am: 07. Nov 2014 15:13 Titel: PhysikGnom Verfasst am: 07. Nov 2014 15:13 Titel: |
 |
|
|
Hallo, ja ok, aber was bedeutet die adjungierte Darstellung? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18188
|
 TomS Verfasst am: 07. Nov 2014 22:32 Titel: TomS Verfasst am: 07. Nov 2014 22:32 Titel: |
 |
|
Was meinst du mit "bedeutet"?
Eine Gruppe ist ja zunächst eine abstrakte Menge von Objekten, zwischen denen eine Beziehung * mit bestimmten Eigenschaften besteht. Jetzt kann man dies auch konkret darstellen. Man realisiert also die Gruppenelemente (z.B.) als Matrizen, die auf einen Vektorraum wirken. Diese Darstellung ist aber nicht eindeutig, d.h. man kann verschiedene Darstellungen der selben Gruppe finden.
Im Falle der SU(2) kann man diese Darstellungen speziell mit j = 0, 1/2, 1, 3/2, ... durchnummerieren (j entspricht physikalisch einem Drehimpuls oder Spin). Der Vektorraum hat dabei die Dimension 2j+1.
Im Falle von Liegruppen sind zwei Darstellungen ausgezeichnet: die Fundamentaldarstellung ist die "treue" Darstellung mit der kleinstmöglichen Dimension des Vektorraumes. Die adjungierte Darstellung ist die Darstellung, in der der Vektorraum gerade durch die Liealgebra selbst gegeben ist.
Das "bedeutet" aber mathematisch zunächst noch gar nichts.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
PhysikGnom

Anmeldungsdatum: 04.11.2014
Beiträge: 77
|
 PhysikGnom Verfasst am: 08. Nov 2014 13:11 Titel: PhysikGnom Verfasst am: 08. Nov 2014 13:11 Titel: |
 |
|
Hoi, ja aber im Eichpotential hab ich ja so einen Ausdruck wie  , (wobei die , (wobei die 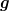 dann die "Eichfreiheit" ist? oder was bedeutet z.B. dann die "Eichfreiheit" ist? oder was bedeutet z.B. = \omega_{ug}(R_{g*}X)=g^{-1}\omega_{u}(X)g) ? Oder ist das einfcah nur die adjungierte Darstellung der Lie Algebra wertigen eins-form? ? Oder ist das einfcah nur die adjungierte Darstellung der Lie Algebra wertigen eins-form? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18188
|
 TomS Verfasst am: 08. Nov 2014 14:17 Titel: TomS Verfasst am: 08. Nov 2014 14:17 Titel: |
 |
|
| PhysikGnom hat Folgendes geschrieben: | Hoi, ja aber im Eichpotential hab ich ja so einen Ausdruck wie  , wobei die , wobei die 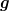 dann die "Eichfreiheit" ist? dann die "Eichfreiheit" ist? |
Genau das ist die Form der adjungieren Darstellung. g ist ein Element der Gruppe.
Allerdings spielt das Eichfeld A eine Sonderrolle, weil es zwar punktweise aussieht wie ein Element der Liealgebra, also

aber eben nicht entsprechend der Liealgebra transformiert
g^{-1})
Wir erinnern uns, für die Algebra gilt

Was entsprechend der Liealgebra transformiert ist die kovariante Ableitung

Es gibt weitere Objekte, die entsprechend der Liealebra transformieren, nämlich Feldstärken

und Ströme.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
PhysikGnom

Anmeldungsdatum: 04.11.2014
Beiträge: 77
|
|
 |
|
















 Und warum muss die Kondition
Und warum muss die Kondition 
