| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 14. Dez 2021 08:41 Titel: FAQ - kosmologische u. grav. Rotverschiebung |
 |
|
Üblicherweise wird die kosmologische Rotverschiebung über die Zeitdilatation motiviert, oder man betrachtet Impuls bzw. Wellenzahlvektor entlang einer lichtartigen Geodäten. Letzteres entspricht der Näherung der geometrischen Optik, in der Geodäten als Normalen auf den Wellenfronten, d.h. Flächen identischer Phase erscheinen.
Prinzipiell ist die Berechnung der kosmologischen Rotverschiebung jedoch mittels direkter Lösung der Wellengleichung auf dem Hintergrund einer Metrik, die ein expandierendes Universum beschreibt, möglich. Dabei beschränke ich mich auf ein flaches Universum mit K = 0, da nur hier mit ebenen Wellen argumentiert werden kann.
Ausgangspunkt ist die Wellengleichung (Klein-Gordon-Gleichung) eines masselosen Skalarfeldes
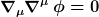
 steht für den 4-dim. Laplace-Beltrami-Operator, d.h. die Verallgemeinerung von  auf gekrümmte Mannigfaltigkeiten. Für eine bekannte Lösung der Einsteinschen Feldgleichungen folgt der Laplace-Beltrami-Operator aus der Metrik gemäß
Unter Verwendung der Friedmann-Robertson-Walker-Metrik
)
 = \sqrt{1 - Kr^2}, \; K = 0, \pm 1)
für ein homogenes und isotropes Universum sowie der adiabatischen Näherung reduziert sich dies auf
})
wobei }) für den von a(t) abhängigen Laplace-Beltrami-Operator auf einem für K = 0 je Zeit t flachen 3-Raum steht.
Die Expansion wird mittels des Skalenfaktors a(t) beschrieben. In der adiabatischen Näherung betrachtet man genügend kurze Zeiträume, innerhalb derer jeweils sehr viele Schwingungen stattfinden, jedoch der Skalenfaktor näherungsweise konstant bleibt, d.h.
Nun setzt man über diesen Zeitraum
und vergleicht Skalenfaktoren und Lösungen der Wellengleichung für zwei verschiedene Zeiträume.
Man definiert
)
und erhält für K = 0 ebene Wellen gemäß
 = e^{i(kx - \omega_a t)})
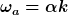
Dies bedeutet, dass vermöge der Zeitabhängigkeit von a(t) ausgehend von einer Lösung mit
 = (\omega(t_0) = k, k^i))
eine neue Lösung zu einem anderen Zeitpunkt mit
 = (\omega(t) = \alpha k, k^i))
resultiert.
Zuletzt folgt die bekannte kosmologische Rotverschiebung direkt mittels Vergleich der Frequenzen
}{\omega(t)} = \frac{k}{\alpha k} = \frac{a}{a_0} )
Eine kovariante Definition der Frequenz Omega als skalare Größe für einen Beobachter mit Vierergeschwindigkeit u folgt mittels
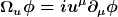
Dies gilt auch, wenn die o.g. adiabatische Näherung nicht exakt gültig ist, jedoch in der Umgebung der Messung in guter Näherung eine ebene Welle vorliegt.
Zuletzt bearbeitet von TomS am 10. Nov 2023 10:11, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 10. Nov 2023 10:04 Titel: |
|
|
Analog kann lässt sich auch die gravitative Rotverschiebung in der Umgebung eines Planeten, eines Sterns oder eines schwarzen Lochs berechnen.
Ausgangspunkt ist wieder die Wellengleichung
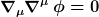
Nun verwenden wir die Schwarzschildmetrik
 \cdot dt^2 - f^{-1}(r) \cdot dr^2 - r^2 \cdot d\Omega^2 )
 = 1 - \frac{2M}{r})
wobei wir später rein radiale Wellenfronten betrachten und damit den Winkel-Term Null setzen. Dies gilt insbs. für näherungsweise ebene Wellen im Labormaßstab.
Die o.g. Wellengleichung führt mittels Substitution
)
 )
sowie dem Separationsansatz
 = \frac{F_l(t, r)}{r} \, Y_{lm}(\Omega))
auf
 = 0)
)
 = \left( 1 - \frac{2M}{r} \right) \left( \frac{l(l+1)}{r^2} + \frac{2M}{r^3}\right))
Im Falle von Skalarfeldern dürfen wir uns auf l=0 konzentrieren, im Falle elektromagnetischer d.h. Dipolfelder ist l=1 der erste nicht-verschwindende Term. Eine allgemeine Lösung erhält man durch Multipolentwicklung.
(Dies ist übrigens exakt die Gleichung, die Hawking zur Berechnung der nach ihm benannten Strahlung betrachtet hat).
Die Lösungen sind bekannt, jedoch sehr kompliziert. Wir benötigen für den folgenden Spezialfall jedoch nur die Zeitabhängigkeit. Wir führen einen weiteren Separationsansatz durch, nämlich
 = e^{-i\omega_l t} \, F_l(r))
setzen nun l=0 und erhalten die Eigenwertgleichung
 = 0)
)
Im Folgenden berechnen wir wieder die beobachtete Frequenz für einen bei Radius r stationären Beobachter mit Vierergeschwindigkeit
 = (f^{-1/2}(r), 0) )
mittels
Im Allgemeinen benötigen wir dazu
 \, \phi_{lm})
mit einer Funktion
 )
(die lokal und für genügend große Radien näherungsweise auf ebene Wellen führt: wir wissen, dass dies nahes des Horizontes sicher nicht zutrifft)
Für unsere speziellen stationären Beobachter gilt jedoch
d.h. sie messen die Frequenz omega um den Faktor
 = \frac{1}{\sqrt{1-\frac{2M}{r}}})
blauverschoben.
Es gilt
 = 1)
 = \infty)
omega entspricht also der Frequenz, die ein stationärer Schwarzschild-Beobachter im Unendlichen messen würde:
Am Horizont divergiert die Blauverschiebung.
Für zwei stationäre Beobachter bei unterschiedlichen Radien argumentiert man umgekehrt und erhält aus dem Verhältnis der so bestimmten Omegas die bekannte Rotverschiebung
}{\Omega(r_2)} = \sqrt{\frac{f(r_2)}{f(r_1)}})
Speziell für die Schwarzschildmetrik sowie stationäre Beobachter folgt die korrekte Rotverschiebung glücklicherweise ohne Lösung der radialen Differentialgleichung.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 13. Nov 2023 15:31, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 13. Nov 2023 10:04 Titel: |
|
|
Noch einige Anmerkungen:
Konsistenzprüfung: für
soll lokal näherungsweise die geometrische Optik gelten, d.h. der (für l=0 rein radiale) Wellenvektor
 )
entspricht dem lichtartigen Viererimpuls eines Photons und damit zugleich der Tangentenvektor an dessen Geodäte, die senkrecht auf den Wellenfronten steht. Damit gilt
 \, \omega)
Für die Vierergeschwindigkeit eines in der Schwarzschild-Geometrie radial frei fallen Beobachter gelten die Gleichungen
 = 1 - \frac{r_S}{r} )
^2 + f = \epsilon^2)
und damit
 = \left(\epsilon f^{-1}, \pm \sqrt{\epsilon^2 - f} \right))
Es gilt
 < 1)
Wählt man die Anfangsbedingung
 = f_0)
sowie das negative Vorzeichen der Wurzel, so folgt
 = (\sqrt{f_0} f^{-1}, -\sqrt{f_0 - f}))
 = (f_0^{-1/2}, 0))
d.h. wir sprechen über eine Beobachter, der aus der Ruhelage von diesem Punkt aus frei zum Zentrum fällt.
Die durch einfallende Beobachter gemessene Frequenz auslaufender Wellen bezeichne ich dann als
 = u^\mu k_\mu = f^{-1} \, (\sqrt{f_0} + \sqrt{f_0 - f}) \, \omega)
wobei die Argumente für den Radius stehen, von dem aus dem Beobachter (dort zunächst stationär) frei fällt, sowie für den kleineren Radius, an dem letztlich die Messung erfolgt.
Für
gilt erwartungsgemäß
 = \omega)
 = \infty)
 = f_0^{-1/2} \omega)
 > \Omega(r_0^\prime|_{r_0 > r_0^\prime}, r))
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
