| Autor |
Nachricht |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 14. Jul 2012 23:05 Titel: Tensor verständliche Definition Nima93 Verfasst am: 14. Jul 2012 23:05 Titel: Tensor verständliche Definition |
 |
|
Meine Frage:
Hallo,
Ich versuche jetzt schon seit längerem, zu verstehen, was genau ein Tensor ist. Ich kenne zum Beispiel den Epsilontensor und verstehe auch, wie er funktioniert. Allerdings kann ich mit der allgemeinen Definition von Tensoren einfach nichts anfangen. Was grenzt einen Tensor 2. Stufe von einer Matrix ab? Ich habe gelesen, Alle Tensoren 2. Stufe sind quadratische 3X3-Matrizen, aber nicht alle quadratischen 3x3-Matrizen sind Tensoren. Kann mir vielleicht jemand auf verständliche Art und Weise sagen, was genau das besondere an einem Tensor ist?
viele Grüße
Nima93
Meine Ideen:
Beim Epsilontensor ist es ja so, dass je nach Permutation der Indizes das ganze 0 ergibt oder eben 1. |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 14. Jul 2012 23:39 Titel: pressure Verfasst am: 14. Jul 2012 23:39 Titel: |
 |
|
|
Welche Definition für Tensoren kennst du denn? Tensoren sind i.d.R. allein durch ihr Transformationsverhalten definiert. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Jul 2012 02:59 Titel: TomS Verfasst am: 15. Jul 2012 02:59 Titel: |
 |
|
Das Transformationsverhalten ist das Stichwort. Versuche mal, Skalar und Vektor unter dem Aspekt der Koordinatentransformation, insbs. der Rotation zu verstehen. Dabei soll das Koordinatensystem selbst rotieren.
Eine Rotation wird mathematisch durch die Multiplikation "Rotationsmatrix mit Ortsvektor" beschriebene, also

Ein Skalarfeld (z.B. eine Temperatur) ändert sich bei Rotation nicht, d.h.
 \to \phi(\vec{r}^\prime) = \phi(\vec{r}))
Nun betrachten wir ein Vektorfeld, symbolisiert durch Pfeile im Raum.
 \to A(\vec{r}^\prime) = R^{-1}\,A(\vec{r}))
Das ist sogar anschaulich klar; wenn sich das Bezugssystem, also ein Beobachter, im Uhrzeigersinn dreht, dann sieht es für diesen mit seinem Bezugssystem mitrotierenden Beobachter so aus, als ob sich der Pfeil entgegen dem Uhrzeigersinn dreht.
Ist das so weit verständlich?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
pascht
Gast
|
 pascht Verfasst am: 15. Jul 2012 18:23 Titel: ??? pascht Verfasst am: 15. Jul 2012 18:23 Titel: ??? |
 |
|
| TomS hat Folgendes geschrieben: | Ein Skalarfeld (z.B. eine Temperatur) ändert sich bei Rotation nicht, d.h.
 \to \phi(\vec{r}^\prime) = \phi(\vec{r}))
|
Das wäre sonderbar. Wenn ich eine Platte die auf einer Seite heiss und auf der anderen Seite kalt ist umderehe, ändert sich nichts?
| Zitat: | | Ist das so weit verständlich? |
Eher nicht. |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 15. Jul 2012 18:46 Titel: Nima93 Verfasst am: 15. Jul 2012 18:46 Titel: |
 |
|
Hallo und danke erstmal für die Mühe!
Die erste Formel ist völlig klar, die zweite verstehe ich allerdings auch nicht so ganz... wenn ich ein skalarfeld drehe, drehe ich doch jeden punkt um eine achse, das heißt es müsste doch dasselbe passieren, wie bei einem einzelnen Vektor? Und warum wird ein Vektorfeld mit der inversen Matrix mutlipliziert? Das wäre doch sozusagen die Rückdrehung einer durch die Matrix R verursachten Drehung? |
|
 |
pascht
Gast
|
 pascht Verfasst am: 15. Jul 2012 18:47 Titel: Re: Tensor verständliche Definition pascht Verfasst am: 15. Jul 2012 18:47 Titel: Re: Tensor verständliche Definition |
 |
|
| Nima93 hat Folgendes geschrieben: | Meine Frage:
Hallo,
Ich versuche jetzt schon seit längerem, zu verstehen, was genau ein Tensor ist. Ich kenne zum Beispiel den Epsilontensor und verstehe auch, wie er funktioniert. |
Das ist schon mal ein gutes Beispiel, aber zum anfänglichen Verstehen vielleicht zu komplex.
Ein Tensor ist ein mehrdimensionaler Vektor, dargestellt durch die jeweiligen Koeffizienten für jede Dimension, in einer Matrix. Eine Matrix deswegen, weil sich Transformationen, so kompakter darstellen lassen.
Zu seiner Beschreibung benötigt man also in einem 3D-Raum mehr als 3 Koeffizienten. Diese fasst man zu einer Matrix zusammen.
>
z.Bsp. der Spannungstensor kann eine tangentiale, radiale und axiale Richtungskomponente haben. Projiziert man nun diese drei Komponenten auf ein Achsensystem besteht jede Komponente wiederum aus 3 Koeffizienten. Das ergibt eine 3x3 Matrix, nur mit den _Koeffizienten_
>
s^2 =sT^2 + sR^2 + sA^2 (1)
>
s_i = x_ii*ei + x_ij*ej + x_ik*ek
>
Wobei die s_i durch die Beziehung (1) veknüpft sind. Das ist der Unterschied zu einer blosen Matrix die keinen Tensor dartellt.
>
In der Mathematik interessiert man sich aber nur für das Transformationsverhalten.
> |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Jul 2012 19:04 Titel: TomS Verfasst am: 15. Jul 2012 19:04 Titel: |
 |
|
Nochmla zum Verständnis der Drehung.
Du betrachtest ein Objekt (Skalarfeld = Betrag, Vektorfeld = Betrag und Richtung) an einem Punkt P. Dieser Punkt P hat in einem Koordinatensystem den Koordinatenvektor r, in einem dazu gedrehten Koordinatensystem den Koordinatenvektor r' = Dr.
Im Falle eines Skalarfeldes bleibt der Wert des Feldes der selbe, denn wir betrachten es ja nur in zwei verschiedenen Koordinatensystemen, aber immer am selben Punkt P (die Temperatur an deinem Schreibtisch ändert sich nicht, egal ob der Koordinatenursprung an deinem Schreibtisch ist, oder ob er an meinem Schreibtisch ist).
Im Falle der Drehung eines Vektorfeldes ändert sich aber die Richtung des Vektors bezogen auf die Koordinatenrichtung. Dreht man das Koordinatensystem um einen bestimmten Winkel (z.B. im Uhrzeigersinn), so rotiert sozusagen der Vektor in genau die andere Richtung (entgegen dem Uhrzeigersinn) bezogen auf das Koordinatensystem (stell dich vor einen Pfeil, der genau in deine Blickrichtung zeigt und dreh dich nach rechts, d.h. dreh das Koordinatensystem nach rechts; aus deiner Sicht, d.h. bezogen auf deine neue Blickrichtung hat sich der Pfeil nach links gedreht)
Soweit jetzt klar?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 15. Jul 2012 19:28 Titel: Nima93 Verfasst am: 15. Jul 2012 19:28 Titel: |
 |
|
|
Achso, ja, jetzt ist mir das mit den Drehungen soweit klar... auch was die Definition des Tensors angeht bekomme ich langsam eine Vorahnung. Tensoren sind also im Prinzip quadratische Matrizen mit einem Sonderkriterium, das dafür sorgt, dass die Koeffizienten der Matrix voneinander abhängen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Jul 2012 19:50 Titel: TomS Verfasst am: 15. Jul 2012 19:50 Titel: |
 |
|
Nun, du kennst jetzt die formale Definition eines Vektors (bzw. der Vektorkomponenten) mittels seines Transformationsverhaltens
_{ik}\,A_k)
bzgl. der Rotation eines Koordinatensystems:
_{ik}\,r_k)
Ein Vektor ist dabei speziell ein Tensor erster Stufe.
Ein Tensor zweiter Stufe in n Dimensionen hat nun n*n Komponenten und transformiert entsprechend
_{ik}\,\left(R^{-1}\right)_{jl}\,T_{kl})
Siehe auch hier http://de.wikipedia.org/wiki/Tensor
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 15. Jul 2012 21:00 Titel: Nima93 Verfasst am: 15. Jul 2012 21:00 Titel: |
 |
|
|
Danke für die Hilfe, das hat mir jetzt schon ein gutes Stück weitergeholfen... ich denke den Rest kann ich mir alleine erarbeiten. |
|
 |
pascht
Gast
|
 pascht Verfasst am: 15. Jul 2012 22:56 Titel: Tensorverhalten pascht Verfasst am: 15. Jul 2012 22:56 Titel: Tensorverhalten |
 |
|
| TomS hat Folgendes geschrieben: | Nochmla zum Verständnis der Drehung.
Soweit jetzt klar? |
Nichts ist klar, weil deine Erklärung falsch ist.
>
Tensoren erkennt man am Transformationsverhalten, z.Bsp. gegenüber orthogonalen Transformationen, genannt Drehungen.
>
Dazu betrachten wir z.Bsp. eine lineare Abbildung:
>
R^3->R^3
>
b = T a
>
b_i = t_ij*a_j (Summenkonvention)
>
Nun betrachten wir wie sich a und b bei einer Drehungs-Transformation R(r_ij) verhalten um zu sehen wie sich T bei dieser Transformation verhält. Man erhält a und b aus jeweils einer Drehung, wobei R als Operator zu betrachten ist.
>
a' = R a
>
a = R^-1 a'
>
b' = R b
>
b'_k = r_ki*b_i
>
b'_k = t'_kl*a'_l = r_ki*b_i = r_ki*t_ij*a_j = r_ki* t_ij* r_lj* a'_l
>
t'_kl = r_ki* r_lj * t_ij
>
Das Transformationsverhalten eines Tensors zweiter Stufe. Ein r_ij pro Stufe.
> |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 15. Jul 2012 23:01 Titel: MI Verfasst am: 15. Jul 2012 23:01 Titel: |
 |
|
Vielleicht doch noch mal meine 20 cents zu dem Problem, weil ich da auch extrem lange für gebraucht habe.
Die "working definition" hast du ja jetzt diskutiert. Das Transformationsverhalten ist im Grunde das, was den Tensor in der Physik ausmacht und woran du ihn erkennen kannst. Rein davon kannst du dir häufig überlegen, was für ein Typ von Tensor dein Objekt sein sollte, wenn du dir einfach nur überlegst, wie es eben transformiert.
Da du aber anscheinend gerne mit deinen Matrizen arbeitest, sei gewarnt: Die Matrizenschreibweise führt - gerade wenn man nur die Definition über das Transformationsverhalten nutzt - gerne in die Irre. Ich habe drei Jahre gebraucht zu verstehen, was der Physiker mit seinen Tensoren wirklich möchte.
Lieber bei der Indexschreibweise bleiben und dir darunter die physikalischen Objekte (Vektoren, etc.) vorstellen, als irgendwelche Matrizen.
Der Grund ist auch folgender: Mathematiker mögen die Physikertensordefinition nicht (und ich mochte sie lange Zeit auch nicht).
Bei den Mathematikern ist (in einer von vielen Definitionen!) ein Tensor einfach nur eine Multilinearform über einem Vektorraum und seinem Dual. Wenn du ein bisschen lineare Algebra hattest, dann ist das eine ganz natürliche Definition.
Soll heißen: Ein Tensor in der Mathematik ist eine Abbildung mit p+q Argumenten, die ersten p sind Vektoren aus dem Dualraum und die anderen q sind ganz normale Vektoren, welche in den Grundkörper abbildet.
(Schau dir dazu, wenn du magst, den Abschnitt "(r,s)-Tensorraum" im verlinkten Wikipediaartikel an.)
Die Definition ist abstrakter als die "working definition" über das Transformationsverhalten, je nachdem, wie du aber gepolt bist, kann es sein, dass sie dir besser gefällt.
Mit dieser Definition kann man leicht sehen, dass jede lineare Abbildung ein Tensor ist (Stufe (1,1)), bilineare Abbildungen sind ebenfalls Tensoren (Stufe (0,2)).
Und das ist auch der Grund, warum ich sage: Aufpassen mit der Matrixidee. Wenn du dir eine Basis wählst, kannst du jede lineare Abbildung durch eine Matrix ausdrücken (hier quadratisch, weil die involvierten Vektorräume alle dieselbe Dimension haben müssen). Genauso jede bilineare Abbildung.
Die Matrix kann also den Tensor in einer Basis darstellen, aber so wirklich der Tensor ist sie nicht.
Aus der Definition geht aber hervor, dass jeder Tensor sich eben genauso transformiert, wie es die Transformationsformel beschreibt, die der Physiker als Grundlage nimmt. Und hier liegt genau der Grundgedanke in der Physik: Wir haben es immer mit einem Bezugssystem zu tun (Basiswahl). Das einzige, was wir also wissen müssen ist, wie sich etwas verhält, wenn wir das Bezugssystem wechseln (also die Basis wechseln). Jede physikalische Größe ist verknüpft mit irgendeiner mathematischen Größe - und von all diesen Größen ist die wichtigste generelle Eigenschaft zu wissen, wie sie sich beim Wechsel der Bezugssysteme verändern - also ihren Tensortyp.
Wenn wir nur davon ausgehen, dann brauchen wir uns keine Gedanken darüber machen, wie man denn diese ganzen Größen auch ohne ein Bezugssystem definieren kann - es ergibt einfach keinen vernünftigen Sinn. So etwas kann man also getrost den Mathematikern überlassen  . . |
|
 |
pascht
Gast
|
 pascht Verfasst am: 15. Jul 2012 23:02 Titel: pascht Verfasst am: 15. Jul 2012 23:02 Titel: |
 |
|
| Nima93 hat Folgendes geschrieben: | | Achso, ja, jetzt ist mir das mit den Drehungen soweit klar... auch was die Definition des Tensors angeht bekomme ich langsam eine Vorahnung. Tensoren sind also im Prinzip quadratische Matrizen mit einem Sonderkriterium, das dafür sorgt, dass die Koeffizienten der Matrix voneinander abhängen? |
Das reicht nicht aus. Es muss das Transformationsverhalten wie in meinem Beispiel gezeigt vorhanden sein.
> |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Jul 2012 23:17 Titel: Re: Tensorverhalten TomS Verfasst am: 15. Jul 2012 23:17 Titel: Re: Tensorverhalten |
 |
|
Hallo pascht,
du hast m.E. die Grundidee nicht verstanden.
| pascht hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Ein Skalarfeld (z.B. eine Temperatur) ändert sich bei Rotation nicht, d.h.
 \to \phi(\vec{r}^\prime) = \phi(\vec{r}))
|
Das wäre sonderbar. Wenn ich eine Platte die auf einer Seite heiss und auf der anderen Seite kalt ist umderehe, ändert sich nichts?? |
Nein, es ändert sich tatsächlich nichts, weil ich nicht die Platte drehe, sondern das Koordinatensystem.
Du hast die Definition von Rotation bzw. allgemein von Koordinatentransformationen nicht verstanden. Die Drehung R, so wie ich sie eingeführt habe, rotiert nicht den Körper im Raum, sie rotiert lediglich das Koordinatensystem, also den Koordinatenvektor r, während der Körper ortsfest bleibt. Du rotierst beispielsweise auf deinem Schreibtischstuhl und führst ein Koordinatensystem mit. Natürlich verändern sich die Koordinaten der Schreibtischlampe bzgl. des rotierenden Koordinatensystems (das ist das R, das auf r wirkt), aber der tatsächliche Ort der Schreibtischlampe bezogen auf alle anderen Gegenstände im Universum ändert sich dadurch nicht. Deswegen bleibt der Wert des Skalarfeldes (z.B. der Temperatur) am Ort der Lampe fest, und das ist genau das, was die Gleichung aussage
| pascht hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Nochmla zum Verständnis der Drehung.
Soweit jetzt klar? |
Nichts ist klar, weil deine Erklärung falsch ist. |
Wenn du dir die Mühe machen würdest, meine Beiträge genau zu lesen, dann würdest du sehen, dass ich Beispiele für das Transformationsverhalten eines Tensor nullter Stufe (Skalarfeld), eines Tensor erster Stufe (Vektorfeld) und eines Tensor zweiter Stufe bzgl. einer Rotation R des Koordinatensystems (r) beispielhaft vorgerechnet habe.
Lies dir bitte mal ein beliebiges Buch über Tensoralgebra durch und du wirst genau diese Definiton des Transformationsverhaltens von Tensoren bzw. Tensorfeldern bzgl. Koordinatentransformationen (Rotation, Lorentztransformation, …) finden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 15. Jul 2012 23:39, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 15. Jul 2012 23:38 Titel: TomS Verfasst am: 15. Jul 2012 23:38 Titel: |
 |
|
| Nima93 hat Folgendes geschrieben: | | Achso, ja, jetzt ist mir das mit den Drehungen soweit klar... auch was die Definition des Tensors angeht bekomme ich langsam eine Vorahnung. Tensoren sind also im Prinzip quadratische Matrizen mit einem Sonderkriterium, das dafür sorgt, dass die Koeffizienten der Matrix voneinander abhängen? |
Nein. Tensoren sind Verallgemeinerung von Vektoren mit einem bestimmten Transformationsverhalten - so wie ich es beispielhaft vorgerechnet habe.
Je Index benötigst du eine Transformationsindex:
Skalar: 0 Indizes => kein R
Vektor: 1 Index => ein R
Tensor 2-ter Stufe => 2 Indizes, zwei R
...
Tensor n-ter Stufe: n Indizes => n mal R
(findest du auch im Wikipedia-Artikel)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 16. Jul 2012 03:47 Titel: jh8979 Verfasst am: 16. Jul 2012 03:47 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
 \to \phi(\vec{r}^\prime) = \phi(\vec{r}))
|
Schoen erklaert (wie immer), auch wenn pascht anscheinend nicht sieht, dass er genau dasselbe geschrieben hat wie du. 
Anyway,... kleine Korrektur: Das Gleichheitszeichen auf der rechten Seite ist natuerlich falsch, die Koordinaten sind immer noch transformiert:
 \to \phi(\vec{r}^\prime) = \phi(R \vec{r})) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 16. Jul 2012 07:10 Titel: TomS Verfasst am: 16. Jul 2012 07:10 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | Schoen erklaert (wie immer), auch wenn pascht anscheinend nicht sieht, dass er genau dasselbe geschrieben hat wie du.  |
Danke

| jh8979 hat Folgendes geschrieben: | Anyway,... kleine Korrektur: Das Gleichheitszeichen auf der rechten Seite ist natuerlich falsch, die Koordinaten sind immer noch transformiert:
 \to \phi(\vec{r}^\prime) = \phi(R \vec{r})) |
Nein, das ist doch der Witz!
 \to \phi(\vec{r}^\prime) \stackrel{!}{=} \phi(R \vec{r}))
Die Forderung lautet, dass der Wert des Feldes im transformierten System r' = Rr gleich (!) dem im nicht-transformierten System ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 16. Jul 2012 07:34 Titel: jh8979 Verfasst am: 16. Jul 2012 07:34 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Die Forderung lautet, dass der Wert des Feldes im transformierten System r' = Rr gleich (!) dem im nicht-transformierten System ist. |
Ja eben. Unter Koordinatentransformation (von mir aus Rotation):
 \to \phi'(\vec r) = \phi(R \vec r))
Die Bedingung  = \phi(\vec r)) , wuerde ja aussagen dass das Feld Rotationssymmetrie besitzt, was natuerlich nicht fuer alle Felder stimmt. , wuerde ja aussagen dass das Feld Rotationssymmetrie besitzt, was natuerlich nicht fuer alle Felder stimmt. |
|
 |
Uriezzo
Anmeldungsdatum: 15.09.2011
Beiträge: 281
Wohnort: Großostheim
|
 Uriezzo Verfasst am: 16. Jul 2012 08:10 Titel: Uriezzo Verfasst am: 16. Jul 2012 08:10 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Nein, es ändert sich tatsächlich nichts, weil ich nicht die Platte drehe, sondern das Koordinatensystem.
|
Es sollte auf das gleiche hinauslaufen, ob ich die Platte drehe oder das Koordinatensystem: Eine Drehung der Platte um  entspricht einer Drehung des Koordinatensystems um entspricht einer Drehung des Koordinatensystems um  . .
Die Werte meines Skalarfeldes ändern sich dabei nicht: 20° bleiben beispielsweise 20°. Wohl aber ändern sich die Koordinaten in meinem Koordinatensystem, an dem die 20° auftreten: Das gilt sowohl für den Fall, dass ich die Platte drehe, als auch für den Fall, dass ich das Koordinatensystem drehe.
Es gilt:
 = \phi(\vec{r}))
Der Wert meines neuen Feldes an einem Punkt ) ist gleich dem des alten Feldes am Punkt ist gleich dem des alten Feldes am Punkt 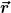 . .
Bei einem Vektorfeld habe ich außer dem Wert (also der Länge des Vektors) auch noch eine Richtung. Die muss ich mitttransformieren und daher ändern sich die Werte der Komponenten meines Vektorfeldes im Gegensatz zu den Werten des Skalarfeldes, die gleich bleiben. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 16. Jul 2012 08:23 Titel: TomS Verfasst am: 16. Jul 2012 08:23 Titel: |
 |
|
| Uriezzo hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Nein, es ändert sich tatsächlich nichts, weil ich nicht die Platte drehe, sondern das Koordinatensystem. |
Es sollte auf das gleiche hinauslaufen, ob ich die Platte drehe oder das Koordinatensystem |
Ich wollte nur zwischen der physikalischen Drehung eines Systems und der Drehung des Koordinatensystems unterscheiden. Aber ich denke, wir sind uns einig.
| Uriezzo hat Folgendes geschrieben: |  = \phi(\vec{r})) |
Uriezzo, jh8979, danke für den Hinweis: jetzt sehe ich den von mir vergessenen Strich bei phi - der ist natürlich wichtig!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Nima93
Anmeldungsdatum: 08.01.2012
Beiträge: 221
|
 Nima93 Verfasst am: 17. Jul 2012 23:40 Titel: Nima93 Verfasst am: 17. Jul 2012 23:40 Titel: |
 |
|
Vielen Dank euch allen, ich werd mir eure Beiträge jetzt sehr oft durchlesen, dann wird die Erleuchtung hoffentlicn nicht allzu lange auf sich warten lassen  |
|
 |
Voessli
Anmeldungsdatum: 14.06.2006
Beiträge: 33
|
 Voessli Verfasst am: 21. Feb 2016 06:28 Titel: Voessli Verfasst am: 21. Feb 2016 06:28 Titel: |
 |
|
|
was ist denn nun ein Tensor ?? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 21. Feb 2016 09:57 Titel: TomS Verfasst am: 21. Feb 2016 09:57 Titel: |
 |
|
s.o. 15. Jul, 19:50.
Ein Beispiel:
Wenn du ein rotiertet Koordinatensystem K' einführst dann ändert sich bzgl. dieses K' der Wert eines Temperaturfekdes nicht, da dieses ein Skalar = ein Tensor nullter Stufe ist.
Die Werte der Komponenten eines Vektors ändern sich gerade so, dass der Vektor selbst entgegen der Drehung des Koordinatensystems rotiert wird; wenn du dich nach links drehst, scheinen sich Richtungen aus deiner Sicht nach rechts zu drehen; ein Vektor ist ein Tensor erster Stufe.
Nun kann man Tensoren höher Stufe konstruieren, wobei hier keine anschauliche Interpretation mehr vorliegen muss. Z.B. kann man die Komponenten des elektrischen und des magnetischen Feldstärkevektors zu einem 4 * 4 Tensor zweiter Stufe zusammenfassen. Das o.g. Transformationsverhalten gilt dann auch für verallgemeinerte "Drehungen" in vier Dimensionen entsprechend der Lorentz-Transformation der speziellen Relativitätstheorie.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Katha90
Gast
|
 Katha90 Verfasst am: 18. Apr 2016 16:52 Titel: Katha90 Verfasst am: 18. Apr 2016 16:52 Titel: |
 |
|
Hallo zusammen,
vielen Dank für eure hilfreichen Erklärungen.
Ich habe eine Frage zum Unterschied zwischen einer Matrix und einem Tensor. Laut Betten (Tensorrechnung für Ingenieure) ist eine Transformationsmatrix kein Tensor, sondern eine Matrix, wenn z.B. eine Drehung eines rechtwinkligen Kartesischen Koordinatensystem in der Ebene betrachtet wird:  (' kennzeichnet die transformierten Koordinaten eines Vektors A und (' kennzeichnet die transformierten Koordinaten eines Vektors A und  ist die Transformationsmatrix ). ist die Transformationsmatrix ).
"Es besteht keine funktionelle Beziehung zwischen zwei Vektoren, sondern es ist nur die Ausdrucksform eines einzigen Vektors in einem anderen (gedrehten) Koordinatensystem."
Im Gegensatz dazu ist T ein Tensor zweiter Stufe. Es gilt  , wobei , wobei  ein abhängig veränderlicher Vektor ist und ein abhängig veränderlicher Vektor ist und  ein unabhängiger veränderlicher Vektor ist. "Der Tensor T erzeugt bei Einwirken auf B einen Vektor A." ein unabhängiger veränderlicher Vektor ist. "Der Tensor T erzeugt bei Einwirken auf B einen Vektor A."
Wie passt das nun mit der vorherigen Erklärung 'was ist ein Tensor?' zusammen, dass der Vektor  mit dem Tensor(?) mit dem Tensor(?)   \rightarrow \phi'(r)) transformiert. transformiert.
Gibt es hierzu vielleicht noch eine andere Erklärung? Ich verstehe nicht warum T ein Tensor ist, aber  nicht.[/latex] nicht.[/latex]
Vielen Dank. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 18. Apr 2016 18:35 Titel: TomS Verfasst am: 18. Apr 2016 18:35 Titel: |
 |
|
Verkürzt gesagt: ein Tensor ist ein Objekt, das unter Transformationen transformiert wird, während spezielle Matrizen gerade die Transformationen darstellen; eine Matrix kann jedoch etwas ganz Allgemeines sein, unabhängig von Transformationen.
Spezielle Transformationsmatrizen sind jedoch selbst Tensoren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 18. Apr 2016 18:43 Titel: franz Verfasst am: 18. Apr 2016 18:43 Titel: |
 |
|
|
Beispiel: der Trägheitstensor gegenüber körperfesten Koordinatensystemen. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 18. Apr 2016 23:17 Titel: Jayk Verfasst am: 18. Apr 2016 23:17 Titel: |
 |
|
@Nima93: Eine Matrix ist nicht mehr als ein rechteckiges Zahlenschema. Eine Matrix kann man nicht transformieren und sie wirkt auch nicht intrinsisch auf Vektoren. Ein Beispiel: Sei 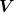 ein endlichdimensionaler reeller Vektorraum. Ich würde ausdrücklich davon abraten, hier in diesem Zusammenhang an den ein endlichdimensionaler reeller Vektorraum. Ich würde ausdrücklich davon abraten, hier in diesem Zusammenhang an den  zu denken, da dieser im Gegensatz zu einem allgemeinen Vektorraum eine kanonische Basis besitzt, die die ganze Diskussion etwas verschleiern würde. Nun nehmen wir zwei verschiedene Basissysteme zu denken, da dieser im Gegensatz zu einem allgemeinen Vektorraum eine kanonische Basis besitzt, die die ganze Diskussion etwas verschleiern würde. Nun nehmen wir zwei verschiedene Basissysteme _i, (f_i)_i) , die durch eine Basiswechselmatrix , die durch eine Basiswechselmatrix _{i,j}) beschrieben werden, d.h. beschrieben werden, d.h. _i \rightarrow (f_i)_i} \operatorname{id}_V) , also , also  . Ein Endomorphismus . Ein Endomorphismus  wird dann bezüglich dieser Basissysteme durch seine Darstellungsmatrizen wird dann bezüglich dieser Basissysteme durch seine Darstellungsmatrizen  \to (e_i)} \varphi =: \Psi^{(e)}) , ,  \to (f_i)} \varphi =: \Phi^{(f)}) beschrieben. beschrieben.
(Anmerkung zur Notation: Für einen allgemeinen Endomorphismus 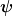 meine ich mit meine ich mit  \to (\beta_i)} \psi =: \Psi) die Darstellungsmatrix bezüglich der Basissysteme b und beta, d.h. die quadratische Matrix, die die Darstellungsmatrix bezüglich der Basissysteme b und beta, d.h. die quadratische Matrix, die  erfüllt. Im Bosch würde das als erfüllt. Im Bosch würde das als  ; (\beta_i)}) notiert werden, soweit ich mich erinnere. Entscheidend ist, daß man nicht notwendigerweise zweimal dasselbe Basissystem verwenden muß und somit Darstellungsmatrizen und Basiswechselmatrizen in einer einheitlichen Notation unterbringt) notiert werden, soweit ich mich erinnere. Entscheidend ist, daß man nicht notwendigerweise zweimal dasselbe Basissystem verwenden muß und somit Darstellungsmatrizen und Basiswechselmatrizen in einer einheitlichen Notation unterbringt)
Dann gilt jedenfalls der folgende wichtige Zusammenhang:
} = A^{-1} \cdot \Phi^{(e)} \cdot A) . .
Angenommen nun,  ist nicht ein Endomorphismus, sondern eine Bilinearform, dann hat diese die Darstellungsmatrix ist nicht ein Endomorphismus, sondern eine Bilinearform, dann hat diese die Darstellungsmatrix } = (B^{(e)}_{ij})_{i,j}) , die durch ihre Eigenschaft , die durch ihre Eigenschaft
 \equiv \Phi^{(e)}_{i j})
definiert ist. Analog für }) . Dann gilt der Zusammenhang: . Dann gilt der Zusammenhang:
} = A^T \cdot \Phi^{(e)} \cdot A) , ,
d.h. anstelle der inversen Matrix steht die transponierte Matrix! Aber die Transponierte einer Transformationsmatrix ist allgemein nicht identisch mit ihrer Inversen. Identisch sind sie genau dann, wenn man eine sog. orthogonale Transformation hat. Wenn man sich aber für allgemeine Basiswechsel interessiert, was spätestens in der Relativitätstheorie der Fall ist, muß man sich mit sowas befassen.
Das ist mit Transformationsverhalten gemeint.
Einfacheres Beispiel: Die Komponenten eines Vektors ändern sich gemäß } = A \cdot v^{(e)}) . Sagen wir nun, wir haben eine Linearform, d.h. einen Kovektor, . Sagen wir nun, wir haben eine Linearform, d.h. einen Kovektor,  , den wir als Spaltenvektor darstellen wollen (Zeilenvektor wäre üblicher, würde aber den Punkt nicht gut verdeutlichen). Dann ist bezüglich jeder Basis , den wir als Spaltenvektor darstellen wollen (Zeilenvektor wäre üblicher, würde aber den Punkt nicht gut verdeutlichen). Dann ist bezüglich jeder Basis  \equiv (\alpha^{(e)})^T \cdot v^{(e)}) , d.h. da , d.h. da } = A \cdot v^{(e)}) , muß , muß })^T = (\alpha^{(e)})^T \cdot A^{-1}) , d.h. , d.h. } = (A^{-1})^T \cdot \alpha^{(e)}) . An die Stelle von A tritt also die Transponiert-Inverse! . An die Stelle von A tritt also die Transponiert-Inverse!
Übrigens muß man sich diese Regeln nicht unbedingt merken, denn es gibt eine sehr gute Koordinaten-Notation dafür: Mache Indizes basis-spezifisch, also verwende z.B.  für die Basis für die Basis _i) und und  für die Basis für die Basis _i) . Dann ist . Dann ist  und und ^{\mu}{}_{\mu'}) (d.h. es ist wichtig, ob gestrichen oben oder unten steht!) und die Wahl der richtigen Transformation folgt automatisch über die Stellung der Indizes (so, daß man nur über oben-unten oder unten-oben kontrahiert): (d.h. es ist wichtig, ob gestrichen oben oder unten steht!) und die Wahl der richtigen Transformation folgt automatisch über die Stellung der Indizes (so, daß man nur über oben-unten oder unten-oben kontrahiert):
- Endomorphismen gibt man die Indexstellung  . In der Tat ist . In der Tat ist
^{\mu'}{}_{\mu} A^{\nu}{}_{\nu'} M^\mu{}_\nu ) . .
- Bilinearformen gibt man die Indexstellung  . In der Tat ist . In der Tat ist

In der Physik wird diese Indexstellung meistens nur im Zusammenhang mit der Relativitätstheorie (also in SRT, ART, Elektrodynamik, QFT) verwendet. In der Differentialgeometrie verwendet man sie dagegen sehr häufig.
Einen Tensor von Rang (r, s) (kovariant von Rang r, kontravariant von Rang s) ist dann einfach so ein Objekt, das r untere und s obere Indizes hat, d.h. Indizes, die mit den entsprechenden Transformationsmatrizen gemäß ihrer Stellung transformiert werden. Endomorphismen sind also Tensoren von Rang (1, 1), Bilinearformen sind Tensoren von Rang (2, 0). Beide lassen sich durch Matrizen darstellen. Für höherrangige Tensoren bräuchte man dann eben quaderförmige Zahlenschemata usw.
Da Franz den Trägheitstensor ins Spiel gebracht hat: Wenn Du schonmal davon gehört hast, wirst Du sicher wissen, daß der Trägheitstensor zwei Funktionen erfüllt: Zum einen ) als Bilinearform bzw. quadratische Form, zum anderen als als Bilinearform bzw. quadratische Form, zum anderen als  als Endomorphismus. Das ist jedenfalls wichtig, wenn man nicht-orthogonale Basiswechsel betrachtet (was aber in der klassischen Mechanik nicht so wichtig ist; deswegen wird darauf auch in der Regel nicht eingegangen). als Endomorphismus. Das ist jedenfalls wichtig, wenn man nicht-orthogonale Basiswechsel betrachtet (was aber in der klassischen Mechanik nicht so wichtig ist; deswegen wird darauf auch in der Regel nicht eingegangen).
Übrigens kann man Bilinearformen und Endomorphismen miteinander identifizieren (sogenanntes Indexziehen bzw. musikalischer Isomorphismus oder flat/sharp-Isomorphismus) und auch generell Tensoren, für die r+s gleich ist. Dafür braucht man aber ein (Pseudo)skalarprodukt. In der klassischen Mechanik ist das das ganz normale euklidische Skalarprodukt, in der Relativitätstheorie die so genannte Metrik bzw. der metrische Tensor. Trotzdem ist es natürlich für eine Berechnung wichtig zu wissen, ob man jetzt gerade an den kovarianten oder kontravarianten Komponenten eines Tensors interessiert ist, sonst bekommt man einfach ein falsches Ergebnis.
Man kann Tensoren auch als Objekte definieren, die mit entsprechenden Vektoren bzw. Kovektoren kontrahiert werden können, d.h.
) , wobei V* der Dualraum, also der Vektorraum der dazugehörigen Kovektoren, ist. Man kann zeigen, daß diese Definitionen (und noch eine ganz abstrakte Version aus der Algebra, die Tensoren über die "universelle Abbildungseigenschaft" definiert) alle gleichwertig sind. , wobei V* der Dualraum, also der Vektorraum der dazugehörigen Kovektoren, ist. Man kann zeigen, daß diese Definitionen (und noch eine ganz abstrakte Version aus der Algebra, die Tensoren über die "universelle Abbildungseigenschaft" definiert) alle gleichwertig sind. |
|
 |
Katha90
Gast
|
 Katha90 Verfasst am: 19. Apr 2016 09:59 Titel: Katha90 Verfasst am: 19. Apr 2016 09:59 Titel: |
 |
|
Aah, der entscheidende Hinweis ist: ein Tensor wird transformiert!
Nach folgender Transformationsvorschrift:

Das kann ich mit  zeigen. Während das mit der Transformationsmatrix zeigen. Während das mit der Transformationsmatrix  nicht funktioniert. nicht funktioniert.
Kann man also sagen, dass ein Vektor mit Hilfe der Transformationsmatrix nur in ein anderes Koordinatensystem abgebildet wird, während ein Tensor so eine Art Funktion ist, die für ein  ein ein  berechnet? berechnet? |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 19. Apr 2016 16:31 Titel: Jayk Verfasst am: 19. Apr 2016 16:31 Titel: |
 |
|
| Katha90 hat Folgendes geschrieben: | Aah, der entscheidende Hinweis ist: ein Tensor wird transformiert!
Nach folgender Transformationsvorschrift:
 |
Im allgemeinen nicht, siehe meinen Beitrag oben. Die Vorschrift, die Du angegeben hast, ist gültig für Tensoren kontravariant von Rang 2, kovariant von Rang 0. Die sind eher selten, aber z.B. der Feldstärketensor wird manchmal mit dieser Konvention gewählt (ich bevorzuge eher, die doppelt kovarianten Komponenten anzugeben).
Für Bilinearformen, also Tensoren kovariant von Rang 2 und kontravariant von Rang 0, müßtest Du in beiden "Brüchen" Zähler und Nenner vertauschen.
Für Endomorphismen, also Tensoren ko- und kontravariant jeweils von Rang 1, müßtest Du in dem Bruch für den unteren Index Zähler und Nenner vertauschen.
Allgemein:
für einen oberen Index 
für einen unteren Index 
Wenn Du den Tensortyp durch die Indexstellung ausdrückst, kannst Du das Transformationsverhalten mechanisch angeben, weil die Indexstellung nur eine Möglichkeit zuläßt (die x haben obere Indizes und ein oberer Index im Nenner zählt wie ein unterer Index). Ansonsten mußt Du mitdenken. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 19. Apr 2016 16:47 Titel: Jayk Verfasst am: 19. Apr 2016 16:47 Titel: |
 |
|
Zumindest Tensoren, die kovariant von Rang [beliebig] und kontravariant von Rang 0 oder 1 sind, kann man eine geometrische Deutung angeben:
Tensor kovariant Rang 1, kontravariant Rang 0: Eine lineare Abbildung, die einen Vektor auf eine Zahl abbildet. Also eine Linearform.
Tensor kovariant Rang 2, kontravariant Rang 0: Eine bilineare Abbildung, die zwei Vektoren auf eine Zahl abbildet. Also eine Bilinearform, z.B. ein Skalarprodukt ist so ein Tensor.
Tensor kovariant Rang 3, kontravariant Rang 0: Eine trilineare Abbildung, die drei...
Tensor kovariant Rang 1, kontravariant Rang 1: Eine lineare Abbildung, die einen Vektor auf einen Vektor abbildet. Also ein Endomorphismus.
Tensor kovariant Rang 2, kontravariant Rang 1: Eine bilineare Abbildung, die zwei Vektoren auf einen Vektor abbildet.
Um kontravariant von höherem Rang zu interpretieren, kann man sich der universellen Abbildungseigenschaft bedienen: Ein Tensor kovariant von Rang 2 nimmt zwei Vektoren entgegen, bezüglich derer er bilinear abbildet. Stattdessen könnte man auch sagen, er nimmt einen Tensor kontravariant von Rang 2 entgegen, den er linear (nicht bilinear!) abbildet. Zum Beispiel sei mal 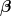 eine Bilinearform. Dann ist eine Bilinearform. Dann ist  = 2 \beta (\vec x , \vec y ) = \beta (\vec x, 2 \vec y)) , das heißt , das heißt  . Ein allgemeiner Tensor kovariant von Rang 2 ist aber nicht von der Form . Ein allgemeiner Tensor kovariant von Rang 2 ist aber nicht von der Form  , sondern , sondern  (mit endlich vielen Gliedern; in der QM bzw. der Funktionalanalysis läßt man auch unendlich viele Glieder zu, weil die Hilberträume meistens unendlichdimensional sind: Dort werden Tensoren u.a. zur Beschreibung von Mehrteilchensystemen benutzt und die Tatsache, daß ein allgemeiner Tensor eine Summe von solchen Termen ist, läßt sich als Verschränkung interpretieren). (mit endlich vielen Gliedern; in der QM bzw. der Funktionalanalysis läßt man auch unendlich viele Glieder zu, weil die Hilberträume meistens unendlichdimensional sind: Dort werden Tensoren u.a. zur Beschreibung von Mehrteilchensystemen benutzt und die Tatsache, daß ein allgemeiner Tensor eine Summe von solchen Termen ist, läßt sich als Verschränkung interpretieren).
Daraus ergibt sich die Interpretation:
Ein Tensor kontravariant von Rang 2, kovariant von Rang 0, ist eine lineare Abbildung, die eine Bilinearform auf eine Zahl abbildet.
Ein Tensor kontravariant von Rang 2, kovariant von Rang 1, ist eine lineare Abbildung, die eine Bilinearform auf einen Vektor abbildet.
usw.
Ein Vektor ist nicht abhängig von einem Koordinatensystem (d.h. der Wahl einer Basis), aber seine Komponenten sind es und sie transformieren sich auf die gegebene Weise. Alternativ sagt man, der Vektor transformiere sich auf eine bestimmte Weise.
Beim Tensor ist es genauso (insbesondere ist es 100% richtig zu sagen, ein Vektor sei ein Spezialfall eines Tensors, was für eine Matrix nicht richtig ist): Der Tensor ist eine Abbildung, seine Komponenten transformieren sich auf eine bestimmte Weise. Alternativ sagt man, der Tensor transformiere sich auf eine bestimmte Weise.
Du hast wohl versucht, Tensoren und Vektoren gegenüberzustellen, aber eine solche Gegenüberstellung gibt es nicht, da Vektoren Tensoren kontravariant von Rang 1 sind. |
|
 |
|
|
















 .
.
