| Autor |
Nachricht |
| TomS |
 Verfasst am: 18. Nov 2020 23:23 Titel: Verfasst am: 18. Nov 2020 23:23 Titel: |
|
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Die Argumentation läuft aufs gleiche raus. |
Welche Argumentation meinst du? Ich bin doch auf die Wahl der Anfangsbedingungen oben schon eingegangen. |
Ja, das habe ich inzwischen auch gesehen; sorry. |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 19:23 Titel: Verfasst am: 18. Nov 2020 19:23 Titel: |
|
| Jo, kommt das selbe raus, danke für die ausführlichen Erklärungen! |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 19:13 Titel: Verfasst am: 18. Nov 2020 19:13 Titel: |
|
| Uhrwerk hat Folgendes geschrieben: | Habe jetzt eingesetzt und die ANfangsbedingungen sind erfüllt, aber eine letzte Frage habe ich
)
und
)
hängen bei mir beide sowohl von
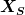 und und
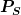
ab. Das ist normal, oder?
|
Ja, das ist normal.
| Zitat: |
Auch, dass ihr Ausdruck sehr lang ist. Der eine ist zB
=(X_{S}-vt_{0})cos(\omega t_{0})cos(\omega t)-\frac{1}{m\omega}(P_{S}-v)sin(\omega t_{0})cos(\omega t)+(X_{S}-vt_{0})sin(\omega t_{0})sin(\omega t)+\frac{1}{m\omega}(P_{S}-v)cos(\omega t_{0})sin(\omega t)+vt)
Kann das passen? Wenn ja, sollte ja damit die Aufgabe erfüllt sein, so wie ich das sehe? |
Ja, vorausgesetzt die Gleichung stimmt, was ich nicht geprüft habe, und zusammen mit der entsprechenden Gl. für p, würde ich damit die Aufgabe als gelöst ansehen. Normalerweise würde man sich allerdings das Leben leichter machen und einfach 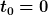 wählen. Wenn die Aufgabe dies gestattet, würde ich das auch tun. Aber es schadet auch nicht, einmal einen etwas komplizierteren Fall gerechnet zu haben. Mit wählen. Wenn die Aufgabe dies gestattet, würde ich das auch tun. Aber es schadet auch nicht, einmal einen etwas komplizierteren Fall gerechnet zu haben. Mit 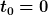 ist die ganze Rechnung deutlich einfacher. Du kannst es ja nochmal zur Probe rechnen und mit deinem Ergebnis vergleichen. ist die ganze Rechnung deutlich einfacher. Du kannst es ja nochmal zur Probe rechnen und mit deinem Ergebnis vergleichen. |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 19:00 Titel: Verfasst am: 18. Nov 2020 19:00 Titel: |
|
Habe jetzt eingesetzt und die ANfangsbedingungen sind erfüllt, aber eine letzte Frage habe ich
)
und
)
hängen bei mir beide sowohl von
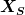 und und
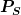
ab. Das ist normal, oder?
Auch, dass ihr Ausdruck sehr lang ist. Der eine ist zB
=(X_{S}-vt_{0})cos(\omega t_{0})cos(\omega t)-\frac{1}{m\omega}(P_{S}-v)sin(\omega t_{0})cos(\omega t)+(X_{S}-vt_{0})sin(\omega t_{0})sin(\omega t)+\frac{1}{m\omega}(P_{S}-v)cos(\omega t_{0})sin(\omega t)+vt)
Kann das passen? Wenn ja, sollte ja damit die Aufgabe erfüllt sein, so wie ich das sehe? |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 18:36 Titel: Verfasst am: 18. Nov 2020 18:36 Titel: |
|
| TomS hat Folgendes geschrieben: | | Die Argumentation läuft aufs gleiche raus. |
Welche Argumentation meinst du? Ich bin doch auf die Wahl der Anfangsbedingungen oben schon eingegangen.
Ich finde im Gegenteil, deine Aussage
| TomS hat Folgendes geschrieben: | Nee, du darfst p nicht in die DGL für x einsetzen und eine DGL zweiter Ordnung in x ableiten;
|
führt in die Irre, da sie scheinbar genau das verbietet, was man machen muß. Diese Behauptung hat für mich keinen unmittelbar erkennbaren Bezug zu der Frage, welche Anfangsbedingungen erlaubt sind. |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 18:28 Titel: Verfasst am: 18. Nov 2020 18:28 Titel: |
|
| Ich habe jetzt meine A und B bestimmt, ich überprüfe kurz ob was sinnvolles rauskommt ,wenn ich einsetze und gebe danach nochmal bescheid, aber schonmal im voraus danke an euch beide! |
|
 |
| TomS |
 Verfasst am: 18. Nov 2020 18:24 Titel: Verfasst am: 18. Nov 2020 18:24 Titel: |
|
Die Argumentation läuft aufs gleiche raus.
Deine Aussage
| index_razor hat Folgendes geschrieben: | Ich eliminiere nicht p, sondern entkopple die Gleichungen. Nachdem ich die Gleichung für x gelöst habe, berechne ich
 = m\dot x(t)) |
führt in die Irre, was du jedoch inzwischen durch
| index_razor hat Folgendes geschrieben: | | A und B sind auch Operatoren ... |
präzisiert hast.
(Dass du das wusstest, war mir schon klar ;-) |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 18:17 Titel: Verfasst am: 18. Nov 2020 18:17 Titel: |
|
TomS, du darfst nicht einfach beliebige Anfangsbedingungen einsetzen. Es muß zu irgendeinem Zeitpunkt gelten  = p_S) und gleichzeitig und gleichzeitig  = x_S) . Dann gilt zu allen Zeitpunkten . Dann gilt zu allen Zeitpunkten
, p_H(t)] = [x_S, p_S].)
Aber bei dir gilt z.B.  = p_S) und und  = 0) . Das geht nicht. . Das geht nicht. |
|
 |
| TomS |
 Verfasst am: 18. Nov 2020 18:16 Titel: Verfasst am: 18. Nov 2020 18:16 Titel: |
|
| index_razor hat Folgendes geschrieben: | Ich eliminiere nicht p, sondern entkopple die Gleichungen. Nachdem ich die Gleichung für x gelöst habe, berechne ich
 = m\dot x(t)) |
Zunächst
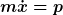
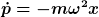
Damit folgt
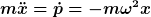
Das hat die Lösung
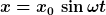
Daraus folgt
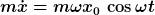
Wegen
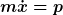
folgt nun
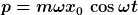
und das ist für Operatoren falsch!
Es wäre dann zum Beispiel
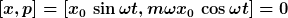 |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 18:01 Titel: Verfasst am: 18. Nov 2020 18:01 Titel: |
|
| Uhrwerk hat Folgendes geschrieben: | Ok, ich habe es theoretisch verstanden, aber mir stellt sich jetzt eine große Frage: Wie sol ich denn die Variablen A und B bestimmen? Klar, die Gleichungen, die du schon genannt hast, sind klar, dass die gelten für 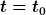 aber ohne Witz, vielleich bin ja dumm, aber es gilt doch aber ohne Witz, vielleich bin ja dumm, aber es gilt doch
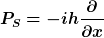 und und 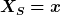
wie soll man denn da vorgehen? Das sind ja keine Werte, sondern Operatoren, aber auf der anderen seite der Gleichung mit meinen A und B stehen ja Werte. Vielleicht könntest du das erklären? |
A und B sind auch Operatoren, genau wie 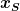 und und 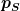 . A und B sind lediglich zunächst nicht explizit bekannt, sondern nur implizit durch die Anfangsbedingungen. Aber alles was du machen mußt um A und B zu betimmen, ist die Matrix . A und B sind lediglich zunächst nicht explizit bekannt, sondern nur implizit durch die Anfangsbedingungen. Aber alles was du machen mußt um A und B zu betimmen, ist die Matrix
 & \sin(\omega t_0)\\ - \omega\sin(\omega t_0)& \omega\cos(\omega(t_0)\end{pmatrix})
zu invertieren. |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 17:54 Titel: Verfasst am: 18. Nov 2020 17:54 Titel: |
|
Ich habe dann ja:
+Bsin(\omega t_{0})+vt_{0})
und
+\omega Bcos(\omega t_{0})+v) |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 17:47 Titel: Verfasst am: 18. Nov 2020 17:47 Titel: |
|
Ok, ich habe es theoretisch verstanden, aber mir stellt sich jetzt eine große Frage: Wie sol ich denn die Variablen A und B bestimmen? Klar, die Gleichungen, die du schon genannt hast, sind klar, dass die gelten für 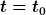 aber ohne Witz, vielleich bin ja dumm, aber es gilt doch aber ohne Witz, vielleich bin ja dumm, aber es gilt doch
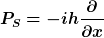 und und 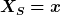
wie soll man denn da vorgehen? Das sind ja keine Werte, sondern Operatoren, aber auf der anderen seite der Gleichung mit meinen A und B stehen ja Werte. Vielleicht könntest du das erklären? Wie gesagt, es ist das erste mal ,dass ich sowas mit Operatoren mache. |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 17:38 Titel: Verfasst am: 18. Nov 2020 17:38 Titel: |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Nee, du darfst p nicht in die DGL für x einsetzen und eine DGL zweiter Ordnung in x ableiten;
|
Doch, das darf man. |
In der klassischen Mechanik ja, aber doch nicht für Operatoren.
|
Warum nicht? Ich leite 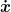 einfach nochmal nach t ab und setze die Gleichung für einfach nochmal nach t ab und setze die Gleichung für 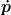 ein. Warum soll das nicht gehen? ein. Warum soll das nicht gehen?
| Zitat: |
Wenn du p vollständig eliminierst bleibt alleine x(t) übrig; wie willst du damit einen nicht-vertauschenden Impulsoperator p(t) darstellen? |
Ich eliminiere nicht p, sondern entkopple die Gleichungen. Nachdem ich die Gleichung für x gelöst habe, berechne ich
 = m\dot x(t)) |
|
 |
| TomS |
 Verfasst am: 18. Nov 2020 17:36 Titel: Verfasst am: 18. Nov 2020 17:36 Titel: |
|
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Nee, du darfst p nicht in die DGL für x einsetzen und eine DGL zweiter Ordnung in x ableiten;
|
Doch, das darf man. |
In der klassischen Mechanik ja, aber doch nicht für Operatoren.
Wenn du p vollständig eliminierst bleibt alleine x(t) übrig; wie willst du damit einen nicht-vertauschenden Impulsoperator p(t) darstellen? |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 17:33 Titel: Verfasst am: 18. Nov 2020 17:33 Titel: |
|
| Uhrwerk hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Uhrwerk hat Folgendes geschrieben: | | Aber wie soll ich das explizit berechnen, wenn ich keine Anfangsbedingungen habe. |
Du hast Anfangsbedingungen: zum Zeitpunkt 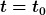 stimmen Heisenberg- und Schrödingeroperatoren überein. stimmen Heisenberg- und Schrödingeroperatoren überein.
Zuerst mußt du allerdings mal die allgemeine Lösung finden. |
Die hab ich:
+Bsin(\omega t) + vt)
ist ja einfach homogene lösung + spezielle. Wie würde ich da jetzt die anfnagsbedingung verwenden die du meintest? wenn ich t0 einsetze, soll also der Schrödingerbild Ortsoperator da stehen?
|
Ja, im Prinzip ergeben
 = x_S, \quad \dot x_H(t_0) = m^{-1} p_S)
zwei Gleichungen für die beiden Unbekannten A und B. Die mußt du lösen.
| Zitat: |
Da sehe ich nicht ganz ,wie das hier zu erreichen ist, das ist doch abhängig davon, welchen wert mein t0 hat oder? |
Ja, die Form der klassischen Bahnkurven x(t) hängt ja auch davon ab, bei welchem 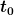 man die Anfangsbedingunegn vorgibt. Was stört dich daran? Der von dir definierte Zeitentwicklungsoperator erfüllt die Anfangsbedingung man die Anfangsbedingunegn vorgibt. Was stört dich daran? Der von dir definierte Zeitentwicklungsoperator erfüllt die Anfangsbedingung
 = 1, \text{für }t=t_0)
Damit folgt
 = x_S, \qquad p_H(t_0) = p_S) |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 17:14 Titel: Verfasst am: 18. Nov 2020 17:14 Titel: |
|
| index_razor hat Folgendes geschrieben: | | Uhrwerk hat Folgendes geschrieben: | | Aber wie soll ich das explizit berechnen, wenn ich keine Anfangsbedingungen habe. |
Du hast Anfangsbedingungen: zum Zeitpunkt 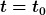 stimmen Heisenberg- und Schrödingeroperatoren überein. stimmen Heisenberg- und Schrödingeroperatoren überein.
Zuerst mußt du allerdings mal die allgemeine Lösung finden. |
Die hab ich:
+Bsin(\omega t) + vt)
ist ja einfach homogene lösung + spezielle. Wie würde ich da jetzt die anfnagsbedingung verwenden die du meintest? wenn ich t0 einsetze, soll also der Schrödingerbild Ortsoperator da stehen? Da sehe ich nicht ganz ,wie das hier zu erreichen ist, das ist doch abhängig davon, welchen wert mein t0 hat oder? |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 17:07 Titel: Verfasst am: 18. Nov 2020 17:07 Titel: |
|
| Uhrwerk hat Folgendes geschrieben: | | Aber wie soll ich das explizit berechnen, wenn ich keine Anfangsbedingungen habe. |
Du hast Anfangsbedingungen: zum Zeitpunkt 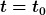 stimmen Heisenberg- und Schrödingeroperatoren überein. stimmen Heisenberg- und Schrödingeroperatoren überein.
Zuerst mußt du allerdings mal die allgemeine Lösung finden. |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 17:04 Titel: Verfasst am: 18. Nov 2020 17:04 Titel: |
|
| Aber wie soll ich das explizit berechnen, wenn ich keine Anfangsbedingungen habe. |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 16:47 Titel: Verfasst am: 18. Nov 2020 16:47 Titel: |
|
| TomS hat Folgendes geschrieben: | Nee, du darfst p nicht in die DGL für x einsetzen und eine DGL zweiter Ordnung in x ableiten;
|
Doch, das darf man. |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 16:45 Titel: Verfasst am: 18. Nov 2020 16:45 Titel: |
|
| Uhrwerk hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Du hast ein lineares Differentialgleichungssystem erster Ordnung in x und p, das du evtl. ja explizit lösen kannst ;-) |
für t0=0 komme ich dann auf
=-\frac{1}{2} \omega^{2}(xt^{2}-\frac{1}{3}vt^{3} ))
|
So löst man kein lineares Gleichungssystem. Du hast beim Integrieren offenbar x als konstant angesetzt. x ist aber eine Funktion der Zeit. Genau diese Funktion suchst du ja.
Edit: Du hast ja offenbar bereits die Gleichung
)
gefunden. Die Frage ist jetzt also nur noch, wie man solche Gleichungen allgemein löst... |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 16:44 Titel: Verfasst am: 18. Nov 2020 16:44 Titel: |
|
| Kannst du mir vielleicht bitte einen Ansatz geben? Ich habe so eine Differentialgleichung für Operatoren noch nie gelöst. |
|
 |
| TomS |
 Verfasst am: 18. Nov 2020 16:31 Titel: Verfasst am: 18. Nov 2020 16:31 Titel: |
|
Nee, du darfst p nicht in die DGL für x einsetzen und eine DGL zweiter Ordnung in x ableiten; x und p sind unabhängige Operatoren.
Du musst wirklich dieses DGL-System in (x,p) lösen und dabei auch berücksichtigen, dass x und p nicht vertauschen. |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 16:24 Titel: Verfasst am: 18. Nov 2020 16:24 Titel: |
|
| TomS hat Folgendes geschrieben: | | Du hast ein lineares Differentialgleichungssystem erster Ordnung in x und p, das du evtl. ja explizit lösen kannst ;-) |
für t0=0 komme ich dann auf
=-\frac{1}{2} \omega^{2}(xt^{2}-\frac{1}{3}vt^{3} ))
für PH stehts ja schon in meinem vorherigen Post.
Kann das stimmen? Wie komme ich von hier auf die Zeitentwickung? |
|
 |
| TomS |
 Verfasst am: 18. Nov 2020 16:02 Titel: Verfasst am: 18. Nov 2020 16:02 Titel: |
|
| Du hast ein lineares Differentialgleichungssystem erster Ordnung in x und p, das du evtl. ja explizit lösen kannst ;-) |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 15:51 Titel: Verfasst am: 18. Nov 2020 15:51 Titel: |
|
ich bekomme dann
=\frac{d}{dt}P_{H}(t)) für die untere Gleichung, wie mache ich dann weiter? für die untere Gleichung, wie mache ich dann weiter? |
|
 |
| Uhrwerk |
 Verfasst am: 18. Nov 2020 15:24 Titel: Verfasst am: 18. Nov 2020 15:24 Titel: |
|
Na,
=\frac{1}{m} P_{H}(t))
=-\frac{\partial V}{\partial x} (X_{H}(t),t))
Aber wie soll mir das hier helfen? |
|
 |
| index_razor |
 Verfasst am: 18. Nov 2020 08:12 Titel: Verfasst am: 18. Nov 2020 08:12 Titel: |
|
| Uhrwerk hat Folgendes geschrieben: | | Außerdem kenne ich ja bereits die beiden Bewegungsgleichungen für Orts- und Impulsoperator. |
Wie lauten denn die Bewegungsgleichungen für X und P? |
|
 |
| TomS |
 Verfasst am: 17. Nov 2020 16:54 Titel: Verfasst am: 17. Nov 2020 16:54 Titel: |
|
x, p sowie
 = \frac{p^2}{2m} + \frac{m\omega^2}{2} (x-vt)^2)
sind deine Operatoren im Heisenbergbild. |
|
 |
| Uhrwerk |
 Verfasst am: 17. Nov 2020 15:16 Titel: Verfasst am: 17. Nov 2020 15:16 Titel: |
|
| Aber kann ich die heisenberggleichung nicht nur für die operatoren im heisenbergbild nutzen? Sonst bekomme ich doch nur erwartungswerte oder nicht? |
|
 |
| TomS |
 Verfasst am: 17. Nov 2020 13:14 Titel: Verfasst am: 17. Nov 2020 13:14 Titel: |
|
| x ist der Ortsoperator. |
|
 |
| Uhrwerk |
 Verfasst am: 17. Nov 2020 12:53 Titel: Verfasst am: 17. Nov 2020 12:53 Titel: |
|
| Ist dann nur x der Ortsoperator oder x-vt? |
|
 |
| TomS |
 Verfasst am: 17. Nov 2020 10:56 Titel: Verfasst am: 17. Nov 2020 10:56 Titel: |
|
| Dein Hamiltonian enthält den üblichen Term p^2 sowie ein (x-vt)^2. Dieses p, x sind dein Impuls- bzw. Ortsoperator. |
|
 |
| Uhrwerk |
 Verfasst am: 17. Nov 2020 10:27 Titel: Verfasst am: 17. Nov 2020 10:27 Titel: |
|
| TomS hat Folgendes geschrieben: | Ob du die Zeitentwicklung integrieren kannst, muss man erst noch sehen. Zunächst solltest du wohl die Heisenbergschen Bewegungsgleichungen für einen Operator A - hier x,p - aufstellen.
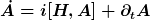 |
Was sind denn in dem Fall meineOrts und Impulsoperatoren. Außerdem kenne ich ja bereits die beiden Bewegungsgleichungen für Orts- und Impulsoperator. |
|
 |
| TomS |
 Verfasst am: 17. Nov 2020 08:35 Titel: Verfasst am: 17. Nov 2020 08:35 Titel: |
|
Ob du die Zeitentwicklung integrieren kannst, muss man erst noch sehen. Zunächst solltest du wohl die Heisenbergschen Bewegungsgleichungen für einen Operator A - hier x,p - aufstellen.
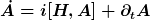 |
|
 |
| Uhrwerk |
 Verfasst am: 16. Nov 2020 18:37 Titel: Zeitentwicklung von Orts- und Impulsoperator Verfasst am: 16. Nov 2020 18:37 Titel: Zeitentwicklung von Orts- und Impulsoperator |
|
Meine Frage:
Hallo,
gegeben sei
=-\frac{\hbar^{2}}{2m}\frac{\partial^{2}}{\partial x^{2}}+\frac{1}{2}m\omega^{2}\left(x-vt\right)^{2})
Bestimme die Zeitentwicklung von Orts- und Impulsoperator
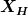 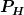
im Heisenbergbild.
Meine Ideen:
Ich bin mir nicht sicher, ob ich die Aufgabe richtig verstehe. Meine Idee wäre jetzt, den Zeitentwicklungsoperator zu berechnen und damit die beiden Operatoren im Heisenbergbild. Aber ich bin skeptisch, ob das die Aufgabe ist. In dem Fall hätte ich
=exp\left(-\frac{i}{\hbar}\int_{t_{0}}^t \ H(t') d t' \right))
angesetzt und überprüft, ob die "Schrödingergleichung" für den Zeitentwicklungsoperator erfüllt ist (ist sie nach meiner Rechnung). Bloß habe ich dann das Problem, dass sich wenn ich dann mit diesen U meine Heisenbergbildoperatoren berechnen will, sich nur der Impulsoperator ändert, dabei müsste gerade der meiner Meinung nach gleich bleiben.
Ich bin wie gesagt ein wenig ratlos, was in der Aufgabe überhaupt verlangt wird, vielleicht kann mir zumindest das jemand sagen xD |
|
 |