| Autor |
Nachricht |
| Myon |
 Verfasst am: 12. Okt 2016 14:24 Titel: Verfasst am: 12. Okt 2016 14:24 Titel: |
|
| Besten Dank für die Antwort! |
|
 |
| TomS |
 Verfasst am: 12. Okt 2016 11:09 Titel: Verfasst am: 12. Okt 2016 11:09 Titel: |
|
| Myon hat Folgendes geschrieben: | -Wenn A ein Drehimpulsoperator ist, kann B=iA keiner sein.
-Wenn A hermitesch ist, kann B=iA nicht hermitesch sein. |
ja, ja

^\dagger = i^\ast A = -iA = -B
<br />) |
|
 |
| Myon |
 Verfasst am: 12. Okt 2016 10:43 Titel: Verfasst am: 12. Okt 2016 10:43 Titel: |
|
Danke. Nur nochmals für meine eigene Klarheit und Sicherheit (die QM liegt bei mir länger zurück, aber ich versuche, einiges aufzufrischen):
-Wenn A ein Drehimpulsoperator ist, kann B=iA keiner sein.
-Wenn A hermitesch ist, kann B=iA nicht hermitesch sein, da seine Erwartungswerte imaginär sind.
Das ist doch richtig? |
|
 |
| TomS |
 Verfasst am: 12. Okt 2016 10:29 Titel: Verfasst am: 12. Okt 2016 10:29 Titel: |
|
Die Verwirrung besteht wohl darin, ob jetzt

oder

gemeint ist.
Ersteres ist darstellungsfrei, letzteres entspricht der Ortsdarstellung. |
|
 |
| Myon |
 Verfasst am: 12. Okt 2016 09:42 Titel: Verfasst am: 12. Okt 2016 09:42 Titel: |
|
Wenn für einen Operator  die Drehimpuls-Kommutatorbeziehung gilt, kann sie doch für einen Operator die Drehimpuls-Kommutatorbeziehung gilt, kann sie doch für einen Operator  nicht gelten? Ebenso kann, wenn nicht gelten? Ebenso kann, wenn  hermitesch ist, hermitesch ist,  nicht hermitesch sein, da seine Erwartungswerte rein imaginär sind? nicht hermitesch sein, da seine Erwartungswerte rein imaginär sind? |
|
 |
| jh8979 |
 Verfasst am: 11. Okt 2016 20:41 Titel: Verfasst am: 11. Okt 2016 20:41 Titel: |
|
| jojo22 hat Folgendes geschrieben: |
In Wirklichkeit ist:  ) . .
Ist damit der Beweis oben hinfällig?
Falls  nicht hermitesch wäre, wäre es auch nicht hermitesch wäre, wäre es auch  , was ja nicht richtig ist. , was ja nicht richtig ist. |
1. Ist die Formel natürlich richtig und die lx, ly und lz erfüllen auch die richtigen Kommutatorrelationen.
2. Wenn Du den Beweis vorher verstanden hättest, dann würdest Du nicht fragen, ob er immer noch richtig ist... |
|
 |
| jojo22 |
 Verfasst am: 11. Okt 2016 20:26 Titel: Verfasst am: 11. Okt 2016 20:26 Titel: |
|
hallo 
vielen Dank für Deine Antwort. Ich antworte leider erst jetzt, da bald Klausur ist und ich mich somit grad in der heißen Phase befinde...
Das Problem war, dass ich im Eifer des Gefechts nicht richtig gelesen habe.
Meine Ursprungsversion ist aber richtig.
Vielen Dank für Deine Mühe 
jojo22 |
|
 |
| Myon |
 Verfasst am: 08. Okt 2016 17:23 Titel: Verfasst am: 08. Okt 2016 17:23 Titel: |
|
| jojo22 hat Folgendes geschrieben: | In Wirklichkeit ist:  ) . . |
Das kann irgendwie nicht sein. Für einen Drehimpuls muss per Definition gelten
 . .
Das wäre beim von dir angegebenen Operator (rechte Seite) nicht der Fall. |
|
 |
| jojo22 |
 Verfasst am: 08. Okt 2016 14:51 Titel: Verfasst am: 08. Okt 2016 14:51 Titel: |
|
hallo :-)
ich sitze grad mal wieder seit längerem bei diesem Thema und habe eine Frage hierzu ...
| jojo22 hat Folgendes geschrieben: |
 f dx^3 = \int g^{\star} (yp_z) f dx^3 - \int g^{\star} zp_y f dx^3 = \\ \int y g^{\star} (p_z) f dx^3 - \int z g^{\star} p_y f dx^3 = \\ \int (y p_z g)^{\star} f dx^3 - \int (z p_y g)^{\star} f dx^3 = \int ((y p_z - z p_y) g)^{\star} f dx^3 = \int (l_x g)^{\star} f dx^3 )
|
hier war ich davon ausgegangen, dass  ) . .
Dies war aber falsch. In Wirklichkeit ist:  ) . .
Ist damit der Beweis oben hinfällig?
Falls  nicht hermitesch wäre, wäre es auch nicht hermitesch wäre, wäre es auch  , was ja nicht richtig ist. , was ja nicht richtig ist. |
|
 |
| jojo22 |
 Verfasst am: 22. Aug 2016 14:50 Titel: Verfasst am: 22. Aug 2016 14:50 Titel: |
|
| Zitat: | | Achso, ja, das ist jetzt nicht unbedingt eine Beweismethode, sondern einfach eine mögliche Definition von "hermitesch". Ich habe es bis jetzt auch nicht so verstanden, daß der Beweis der Hermitezität der Drehimpulsoperatoren Teil der Aufgabe ist. Diese, inklusive der Linearität der Operatoren, haben wir jetzt tatsächlich einfach vorausgesetzt, was auch ok sein sollte. |
Ah okay. Ja, so im Nachhinein denke ich das auch
| Zitat: |
P.S. Vielleicht solltest du mal in einige deiner Formeln weiter oben im Thread Zeilenumbrüche einfügen. Das wird irgendwie anstrengend zu lesen. |
Ja mach ich :-)
| Zitat: |
Trotzdem ist die Frage, woraus man die Linearität ableiten kann, interessant. Ich denke, daß es auf Grund des Superpositionsprinzips und der Interpretation des Zustands als Wahrscheinlichkeitsamplitude wenig Sinn ergibt, nichtlineare Operatoren als Observablen zu betrachten.
Es gibt da auch einen Satz von Wigner, nach dem Symmetrieoperationen, also solche, die die Übergangsamplituden zwischen Zuständen invariant lassen, auf dem Hilbertraum entweder durch lineare, unitäre Operatoren oder durch antilineare, antiunitäre Operatoren dargestellt werden müssen. (Der letztere Fall ist ausgeschlossen, wenn diese Symmetrieoperationen sich stetig in die identische Transformation überführen lassen. Denn diese ist ja unitär und linear.)
Danach wären also die Generatoren der üblichen Symmetrien, wie Raumtranslationen, Drehungen, ... , d.h. Impuls, Drehimpuls, ... hermitesche, lineare Operatoren. |
puh, ja ist sicher interessant. Aber für meine Bedürfnisse schießt das etwas weit übers Ziel hinaus.. :-)
Aber vielen Dank für Deine Hilfe. Dank Dir, ich hab jetzt diese Aufgabe und insbesondere die Dirac-Notation viel besser verstanden  |
|
 |
| index_razor |
 Verfasst am: 22. Aug 2016 12:00 Titel: Verfasst am: 22. Aug 2016 12:00 Titel: |
|
| jojo22 hat Folgendes geschrieben: |
| Zitat: |
Das weiß ich nicht. Wie sieht denn dieser alternative Beweis aus? |
Dann haben wir entweder oben aneinander vorbeigesprochen, oder ich habe das falsch verstanden im Skript.
Also das was ich jetzt schreibe ist nach meinem Verständnis eine andere Methode, eine Hermitizität nachzuweisen:
| Zitat: |
* Ein Operator  ist linear, falls ist linear, falls  = c_1 \hat{A} f_1 + c_2 \hat{A} f_2 )
* Ein Operaor  heißt hermitesch, falls er linear ist und falls heißt hermitesch, falls er linear ist und falls  |
Das hört sich für mich so an, als müsste ich erstmal die Linearität beweisen, und dann den Zusammenhang des zweiten Satzes.
Das haben wir ja so nicht gemacht..?
|
Achso, ja, das ist jetzt nicht unbedingt eine Beweismethode, sondern einfach eine mögliche Definition von "hermitesch". Ich habe es bis jetzt auch nicht so verstanden, daß der Beweis der Hermitezität der Drehimpulsoperatoren Teil der Aufgabe ist. Diese, inklusive der Linearität der Operatoren, haben wir jetzt tatsächlich einfach vorausgesetzt, was auch ok sein sollte.
Trotzdem ist die Frage, woraus man die Linearität ableiten kann, interessant. Ich denke, daß es auf Grund des Superpositionsprinzips und der Interpretation des Zustands als Wahrscheinlichkeitsamplitude wenig Sinn ergibt, nichtlineare Operatoren als Observablen zu betrachten.
Es gibt da auch einen Satz von Wigner, nach dem Symmetrieoperationen, also solche, die die Übergangsamplituden zwischen Zuständen invariant lassen, auf dem Hilbertraum entweder durch lineare, unitäre Operatoren oder durch antilineare, antiunitäre Operatoren dargestellt werden müssen. (Der letztere Fall ist ausgeschlossen, wenn diese Symmetrieoperationen sich stetig in die identische Transformation überführen lassen. Denn diese ist ja unitär und linear.)
Danach wären also die Generatoren der üblichen Symmetrien, wie Raumtranslationen, Drehungen, ... , d.h. Impuls, Drehimpuls, ... hermitesche, lineare Operatoren.
P.S. Vielleicht solltest du mal in einige deiner Formeln weiter oben im Thread Zeilenumbrüche einfügen. Das wird irgendwie anstrengend zu lesen. |
|
 |
| jojo22 |
 Verfasst am: 21. Aug 2016 12:31 Titel: Verfasst am: 21. Aug 2016 12:31 Titel: |
|
| jojo22 hat Folgendes geschrieben: |
* Ein Operator  ist linear, falls ist linear, falls  = c_1 \hat{A} f_1 + c_2 \hat{A} f_2 )
* Ein Operaor  heißt hermitesch, falls er linear ist und falls heißt hermitesch, falls er linear ist und falls  |
Es gilt:
 oder? oder?
Also der zweite Satz würde dann schon mal übereinstimmen in beiden "Beweismethoden". Also die eine, welche wir oben benutzt haben, und die andere, die ich hier erneut zitiert habe.
Aber die Linearität haben wir nie nachgewiesen oder? |
|
 |
| jojo22 |
 Verfasst am: 21. Aug 2016 11:33 Titel: Verfasst am: 21. Aug 2016 11:33 Titel: |
|
| index_razor hat Folgendes geschrieben: |
| Zitat: |
Damit erhalte ich:

|
Das erhältst du ja aus der Vertauschbarkeit von 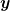 und und  allein. Wichtiger ist das Resultat allein. Wichtiger ist das Resultat

|
Genau. Das meinte ich. Also damit erhalte ich  als Resultat als Resultat 
| Zitat: | Hier:

Du ziehst das i in das erste Argument des Produkts und kehrst dabei das Vorzeichen um. Das folgt daraus:
^\star = i^\star \langle g,f\rangle^\star = -i \langle f, g\rangle ) |
Ah okay. Ich hatte das "i" einfach in die Klammern reingezogen und dadurch hat sich das Vorzeichen umgedreht.
| Zitat: | | Zitat: |
Ich hatte auch noch die alternative Beweismöglichkeit aus meinem Skript erwähnt. Also die hat nichts mit den hier ausführlich aufgeschriebenen Beweisen zu tun!? Also erstmal Beweis der Linearität...
|
Das weiß ich nicht. Wie sieht denn dieser alternative Beweis aus? |
Dann haben wir entweder oben aneinander vorbeigesprochen, oder ich habe das falsch verstanden im Skript.
Also das was ich jetzt schreibe ist nach meinem Verständnis eine andere Methode, eine Hermitizität nachzuweisen:
| Zitat: |
* Ein Operator  ist linear, falls ist linear, falls  = c_1 \hat{A} f_1 + c_2 \hat{A} f_2 )
* Ein Operaor  heißt hermitesch, falls er linear ist und falls heißt hermitesch, falls er linear ist und falls  |
Das hört sich für mich so an, als müsste ich erstmal die Linearität beweisen, und dann den Zusammenhang des zweiten Satzes.
Das haben wir ja so nicht gemacht..?
Wir haben ja nicht die Linearität bewiesen oder eben den zweiten Satz beim Nachweis der Hemitizität von  |
|
 |
| index_razor |
 Verfasst am: 21. Aug 2016 09:24 Titel: Verfasst am: 21. Aug 2016 09:24 Titel: |
|
| jojo22 hat Folgendes geschrieben: |
| Zitat: |
Damit gilt ^t f, g\rangle = \langle f, ABg\rangle = \langle A^tf, Bg\rangle = \langle B^tA^t f, g\rangle) . Jetzt setzt du . Jetzt setzt du  und und  und benutzt, daß beide hermitesch und vertauschbar sind. Was erhältst du dann? und benutzt, daß beide hermitesch und vertauschbar sind. Was erhältst du dann? |
Damit erhalte ich:

|
Das erhältst du ja aus der Vertauschbarkeit von 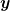 und und  allein. Wichtiger ist das Resultat allein. Wichtiger ist das Resultat

(Dieselbe Reihenfolge der Operatoren links und rechts!)
| Zitat: |
1. und 2. Beweis haben beide den gleichen Beweisweg, nur in einer anderen Notation.
Weil es hat sich so angehört, dass es einen ganz anderen Weg gibt an die Sache heranzugehen,
|
Nein, alles was du im abstrakten Hilbertraum machen kannst, kannst du auch in der Ortsdarstellung, bzw. in jedem beliebigen ) machen. machen.
| Zitat: |
Aber wo benutze ich folgendes:
| Zitat: |
 . . |
|
Hier:

Du ziehst das i in das erste Argument des Produkts und kehrst dabei das Vorzeichen um. Das folgt daraus:
^\star = i^\star \langle g,f\rangle^\star = -i \langle f, g\rangle )
| Zitat: |
Ich hatte auch noch die alternative Beweismöglichkeit aus meinem Skript erwähnt. Also die hat nichts mit den hier ausführlich aufgeschriebenen Beweisen zu tun!? Also erstmal Beweis der Linearität...
|
Das weiß ich nicht. Wie sieht denn dieser alternative Beweis aus?
(Edit: Latex repariert) |
|
 |
| jojo22 |
 Verfasst am: 20. Aug 2016 17:33 Titel: Verfasst am: 20. Aug 2016 17:33 Titel: |
|
Danke. Es ist etwas unübersichtlich geworden, ich versuche es erstmal zusammen zu fassen:
1. Beweis von der Hermitizität von  (lange Version, Ortsdarstellung): (lange Version, Ortsdarstellung):
| jojo22 hat Folgendes geschrieben: |
 f dx^3 = \int g^{\star} (yp_z) f dx^3 - \int g^{\star} zp_y f dx^3 = \\ \int y g^{\star} (p_z) f dx^3 - \int z g^{\star} p_y f dx^3 = \\ \int (y p_z g)^{\star} f dx^3 - \int (z p_y g)^{\star} f dx^3 = \int ((y p_z - z p_y) g)^{\star} f dx^3 = \int (l_x g)^{\star} f dx^3 )
|
2. Beweis von der Hermitizität von  (kurze Version, Dirac-Notation): (kurze Version, Dirac-Notation):

bzw die eine Hälfte:
| Zitat: |
Damit gilt ^t f, g\rangle = \langle f, ABg\rangle = \langle A^tf, Bg\rangle = \langle B^tA^t f, g\rangle) . Jetzt setzt du . Jetzt setzt du  und und  und benutzt, daß beide hermitesch und vertauschbar sind. Was erhältst du dann? und benutzt, daß beide hermitesch und vertauschbar sind. Was erhältst du dann? |
Damit erhalte ich:

_____________
1. Beweis, dass 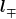 das hermetisch konjugierte von das hermetisch konjugierte von  ist (lange Version, Ortsdarstellung): ist (lange Version, Ortsdarstellung):
\dd x = \int g^\star(l_x f)\dd x \pm i\int g^\star(l_y f)\dd x = \\ \int (l_x g^\star) f\dd x \pm i\int (l_y g^\star) f\dd x = \int (l_x g^\star) f\dd x \pm \int (il_y g^\star) f\dd x = ) ^\star f\dd x \mp \int (il_y g)^\star f\dd x = \\ \int (l_{\mp} g)^\star f\dd x = \\ \int (A^t f)^* g dx^3 )
2. Beweis, dass 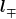 das hermetisch konjugierte von das hermetisch konjugierte von  ist (kurze Version, Dirac-Notation): ist (kurze Version, Dirac-Notation):

1. und 2. Beweis haben beide den gleichen Beweisweg, nur in einer anderen Notation.
Weil es hat sich so angehört, dass es einen ganz anderen Weg gibt an die Sache heranzugehen, als du meintest:
| Zitat: | Du hast an keiner Stelle direkt benutzt, daß
 f(x)\dd x)
ein Integral über den Ortsraum ist. Die einzigen Eigenschaftem, die du benötigst, sind die Linearität in 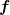 , d.h , d.h

für alle Konstanten  und alle Funktionen und alle Funktionen  , sowie , sowie
 . .
Vielleicht hast du ja Lust und Neigung, denselben Beweis nochmal allein unter Ausnutzung dieser rein abstrakten Eigenschaften des Hilbertraum-Produkts zu führen ohne Bezug auf irrelevante Details der speziellen Ortsdarstellung in einem Funktionenraum. Lehrreich könnte es jedenfalls sein. |
Also das was du in dem eben genannten Zitat meintest, war nichts anderes als mein Beweis: "2. Beweis, dass 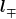 das hermetisch konjugierte von das hermetisch konjugierte von  ist (kurze Version, Dirac-Notation):" ?? ist (kurze Version, Dirac-Notation):" ??
Aber wo benutze ich folgendes:
| Zitat: |
 . . |
Ich hatte auch noch die alternative Beweismöglichkeit aus meinem Skript erwähnt. Also die hat nichts mit den hier ausführlich aufgeschriebenen Beweisen zu tun!? Also erstmal Beweis der Linearität...
___________________
| Zitat: | Langsam,  sind nicht hermitesch. Es gilt sind nicht hermitesch. Es gilt  . Das zu zeigen war doch der Sinn der Aufgabe. . Das zu zeigen war doch der Sinn der Aufgabe. |
Stimmt. Ich meinte nicht "hermitesch", sondern "hermitesch konjugiert". |
|
 |
| index_razor |
 Verfasst am: 20. Aug 2016 16:41 Titel: Verfasst am: 20. Aug 2016 16:41 Titel: |
|
| jojo22 hat Folgendes geschrieben: |
Zur Übersichtlichkeit: Es geht um den Beweis von der Hermitizität von  : :
also du meinst ich soll mit dieser Schreibweise vorgehen:
 und dann analog wie oben, nur eben in dieser anderen Schreibweise ? Das heißt für mich, ich benutze den Dirac-Formalismus und nicht die Ortsdarstellung. und dann analog wie oben, nur eben in dieser anderen Schreibweise ? Das heißt für mich, ich benutze den Dirac-Formalismus und nicht die Ortsdarstellung.
Der andere Teil deiner Aussage ist, dass ich nicht den Multiplikations- und Ableitungsperator benötige. Aber natürlich benutze ich diese Operatoren auch im Dirac-Formalismus. Ich muss ja schauen, was ich vertauschen kann, ob ich z.B.  vor das vor das  ziehen kann usw... ziehen kann usw...
|
Ja, klar benutzt du die Operatoren. Es ist ganz einfach. Der hermitesch konjugierte Operator  zu zu  ist so definiert ist so definiert

Damit gilt ^t f, g\rangle = \langle f, ABg\rangle = \langle A^tf, Bg\rangle = \langle B^tA^t f, g\rangle) . Jetzt setzt du . Jetzt setzt du  und und  und benutzt, daß beide hermitesch und vertauschbar sind. Was erhältst du dann? und benutzt, daß beide hermitesch und vertauschbar sind. Was erhältst du dann?
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Ja das auch. Ich meinte aber eigentlich eher die Linearität (oder eigentlich Sesquilinearität) des Hilbertraumprodukts  . Aber du benötigst auch die Eigenschaften, die du aufgezählt hast. Dann geht es z.B. so . Aber du benötigst auch die Eigenschaften, die du aufgezählt hast. Dann geht es z.B. so

hier habe ich schonmal die Tatsache benutzt, daß 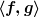 linear in g ist. Weiter geht es dann mit der Hermitezität von linear in g ist. Weiter geht es dann mit der Hermitezität von  und irgendwann brauchst du noch die Antilinearität in f... und irgendwann brauchst du noch die Antilinearität in f... |
Ich glaube das alles versuchen nachzuvollziehen wäre eine gute Erfahrung, aber aufgrund von Zeitoptimierung muss ich ein paar Abstriche machen.
|
Klar, kein Problem. Ich wollte es nur mal erwähnen, weil es wichtig ist.
| Zitat: |
Aber sowohl deine Variante als auch meine laufen auf das selbe hinaus..!? |
Ja, ist absolut dasselbe.
| Zitat: |
Also Beweis, dass  hermitesch ist. hermitesch ist.
Ich würde gerne in inhaltlich in der Nähe meines Skripts bleiben. Also Beweis der Linearität und dass  . Das ist doch vollkommen ausreichend, um eben zu beweisen, dass . Das ist doch vollkommen ausreichend, um eben zu beweisen, dass  hermitesch ist, oder? hermitesch ist, oder?
|
Langsam,  sind nicht hermitesch. Es gilt sind nicht hermitesch. Es gilt  . Das zu zeigen war doch der Sinn der Aufgabe. . Das zu zeigen war doch der Sinn der Aufgabe.
| Zitat: |
Wo ist der Vorteil deiner Variante?
|
Sie ist übersichtlicher und aufs wesentliche beschränkt. Und um den Dirac-Formalismus kommst du wahrscheinlich früher oder später auch nicht herum.
| Zitat: |
Ich bin gerade schon an den Grenzen von meinem Verständnis für diese Thematik.
|
Dafür gibt es ja u.a. dieses Forum. Aber ich habe eher den Eindruck, daß du das ganze eigentlich schon ganz gut auffaßt. Selbst mit Dirac-Formalismus, der ja für dich noch ungewohnt zu sein scheint.
| Zitat: |

|
Sieht schon ganz gut aus. Bis auf den letzten Schritt. Da muß stehen

Das  wirkt also auf wirkt also auf 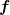 , nicht , nicht 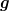 . Nun ist aber nach der Definition des hermitesch konjugierten, der Operator vor dem g auf der rechten Seite gerade . Nun ist aber nach der Definition des hermitesch konjugierten, der Operator vor dem g auf der rechten Seite gerade  . Also gilt . Also gilt 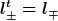 . (Man muß für diese Identifizierung natürlich dafür noch beweisen, daß es nur einen solchen Operator geben kann, aber es ist, denke ich, in Ordnung, wenn du das voraussetzt.) . (Man muß für diese Identifizierung natürlich dafür noch beweisen, daß es nur einen solchen Operator geben kann, aber es ist, denke ich, in Ordnung, wenn du das voraussetzt.)
| Zitat: |
Das ist jetzt also der kurze Beweis, von dem du gesprochen hast oder?
Das hat jetzt nichts damit zu tun, dass ich irgendeine Linearität betrachtet habe oder so. Also der gleiche Beweis wie oben, nur in DiracNotation |
Ja, das habe ich gemeint. Du hast die Linearität des Hilbertraum-Produkts bzgl. des zweiten Arguments benutzt; gleich im ersten Schritt. Und die Antilinearität bzgl. des ersten Arguments im dritten (und vierten) Schritt. |
|
 |
| jojo22 |
 Verfasst am: 20. Aug 2016 16:08 Titel: Verfasst am: 20. Aug 2016 16:08 Titel: |
|
| index_razor hat Folgendes geschrieben: |
Ich meine, du benötigst nicht, daß (x,y,z) = yf(x,y,z)) der Multiplikationsoperator und der Multiplikationsoperator und  der Ableitungsoperator auf den Ortswellenfunktionen ist. Du mußt gar nicht in der Ortsdarstellung rechnen. Das spart dir nicht nur einen Schritt, sondern macht die ganze Rechnung etwas übersichtlicher, weil die wesentlichen benötigten Eigenschaften der Operatoren expliziter hervortreten. (Das ist der ganze Nutzen im abstrakten Dirac/Hilbertraum-Formalismus.) der Ableitungsoperator auf den Ortswellenfunktionen ist. Du mußt gar nicht in der Ortsdarstellung rechnen. Das spart dir nicht nur einen Schritt, sondern macht die ganze Rechnung etwas übersichtlicher, weil die wesentlichen benötigten Eigenschaften der Operatoren expliziter hervortreten. (Das ist der ganze Nutzen im abstrakten Dirac/Hilbertraum-Formalismus.)
|
Zur Übersichtlichkeit: Es geht um den Beweis von der Hermitizität von  : :
also du meinst ich soll mit dieser Schreibweise vorgehen:
 und dann analog wie oben, nur eben in dieser anderen Schreibweise ? Das heißt für mich, ich benutze den Dirac-Formalismus und nicht die Ortsdarstellung. und dann analog wie oben, nur eben in dieser anderen Schreibweise ? Das heißt für mich, ich benutze den Dirac-Formalismus und nicht die Ortsdarstellung.
Der andere Teil deiner Aussage ist, dass ich nicht den Multiplikations- und Ableitungsperator benötige. Aber natürlich benutze ich diese Operatoren auch im Dirac-Formalismus. Ich muss ja schauen, was ich vertauschen kann, ob ich z.B.  vor das vor das  ziehen kann usw... ziehen kann usw...
| index_razor hat Folgendes geschrieben: |
Ja das auch. Ich meinte aber eigentlich eher die Linearität (oder eigentlich Sesquilinearität) des Hilbertraumprodukts  . Aber du benötigst auch die Eigenschaften, die du aufgezählt hast. Dann geht es z.B. so . Aber du benötigst auch die Eigenschaften, die du aufgezählt hast. Dann geht es z.B. so

hier habe ich schonmal die Tatsache benutzt, daß 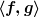 linear in g ist. Weiter geht es dann mit der Hermitezität von linear in g ist. Weiter geht es dann mit der Hermitezität von  und irgendwann brauchst du noch die Antilinearität in f... und irgendwann brauchst du noch die Antilinearität in f... |
Ich glaube das alles versuchen nachzuvollziehen wäre eine gute Erfahrung, aber aufgrund von Zeitoptimierung muss ich ein paar Abstriche machen. Aber sowohl deine Variante als auch meine laufen auf das selbe hinaus..!? Also Beweis, dass  hermitesch ist. hermitesch ist.
Ich würde gerne in inhaltlich in der Nähe meines Skripts bleiben. Also Beweis der Linearität und dass  . Das ist doch vollkommen ausreichend, um eben zu beweisen, dass . Das ist doch vollkommen ausreichend, um eben zu beweisen, dass  hermitesch ist, oder? Wo ist der Vorteil deiner Variante? hermitesch ist, oder? Wo ist der Vorteil deiner Variante?
Ich bin gerade schon an den Grenzen von meinem Verständnis für diese Thematik.

Das ist jetzt also der kurze Beweis, von dem du gesprochen hast oder?
Das hat jetzt nichts damit zu tun, dass ich irgendeine Linearität betrachtet habe oder so. Also der gleiche Beweis wie oben, nur in DiracNotation |
|
 |
| index_razor |
 Verfasst am: 20. Aug 2016 14:32 Titel: Verfasst am: 20. Aug 2016 14:32 Titel: |
|
| jojo22 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Ab hier hast du benutzt, daß 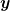 und und  , etc. vertauschen. Und mehr als diese algebraischen Eigenschaften benötigst du auch nicht. Indem du alle Operatoren explizit in der Ortsdarstellung aufschreibst, machst du den Beweis nur komplizierter als er eigentlich sein müßte. , etc. vertauschen. Und mehr als diese algebraischen Eigenschaften benötigst du auch nicht. Indem du alle Operatoren explizit in der Ortsdarstellung aufschreibst, machst du den Beweis nur komplizierter als er eigentlich sein müßte. |
Wie genau meinst du das? Das ich mir hätte einen Schritt sparen können und gleich hätte so schreiben können:
 f dx^3 - \int z g^{\star} p_y f dx^3 = \int (y p_z g)^{\star} f dx^3 - \int (z p_y g)^{\star} f dx^3 ) ? ?
|
Ich meine, du benötigst nicht, daß (x,y,z) = yf(x,y,z)) der Multiplikationsoperator und der Multiplikationsoperator und  der Ableitungsoperator auf den Ortswellenfunktionen ist. Du mußt gar nicht in der Ortsdarstellung rechnen. Das spart dir nicht nur einen Schritt, sondern macht die ganze Rechnung etwas übersichtlicher, weil die wesentlichen benötigten Eigenschaften der Operatoren expliziter hervortreten. (Das ist der ganze Nutzen im abstrakten Dirac/Hilbertraum-Formalismus.) der Ableitungsoperator auf den Ortswellenfunktionen ist. Du mußt gar nicht in der Ortsdarstellung rechnen. Das spart dir nicht nur einen Schritt, sondern macht die ganze Rechnung etwas übersichtlicher, weil die wesentlichen benötigten Eigenschaften der Operatoren expliziter hervortreten. (Das ist der ganze Nutzen im abstrakten Dirac/Hilbertraum-Formalismus.)
| Zitat: |
zu 2.) Also ich habe den einen Beweis schon über die eine Methode gemacht. Du hast jetzt noch eine zweite Variation aufgeschrieben mittelns Linearität... In meinem Skript lautet diese Möglichkeit etwas anders, aber ich denke, der Verfasser des Skripts möchte aufs gleiche hinaus:
* Ein Operator  ist linear, falls ist linear, falls 
* Ein Operaor  heißt hermitesch, falls er linear ist und falls heißt hermitesch, falls er linear ist und falls 
Ist das das was du meinst? |
Ja das auch. Ich meinte aber eigentlich eher die Linearität (oder eigentlich Sesquilinearität) des Hilbertraumprodukts  . Aber du benötigst auch die Eigenschaften, die du aufgezählt hast. Dann geht es z.B. so . Aber du benötigst auch die Eigenschaften, die du aufgezählt hast. Dann geht es z.B. so

hier habe ich schonmal die Tatsache benutzt, daß 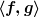 linear in g ist. Weiter geht es dann mit der Hermitezität von linear in g ist. Weiter geht es dann mit der Hermitezität von  und irgendwann brauchst du noch die Antilinearität in f... und irgendwann brauchst du noch die Antilinearität in f... |
|
 |
| jojo22 |
 Verfasst am: 20. Aug 2016 14:03 Titel: Verfasst am: 20. Aug 2016 14:03 Titel: |
|
| index_razor hat Folgendes geschrieben: |
Ab hier hast du benutzt, daß 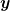 und und  , etc. vertauschen. Und mehr als diese algebraischen Eigenschaften benötigst du auch nicht. Indem du alle Operatoren explizit in der Ortsdarstellung aufschreibst, machst du den Beweis nur komplizierter als er eigentlich sein müßte. , etc. vertauschen. Und mehr als diese algebraischen Eigenschaften benötigst du auch nicht. Indem du alle Operatoren explizit in der Ortsdarstellung aufschreibst, machst du den Beweis nur komplizierter als er eigentlich sein müßte. |
Wie genau meinst du das? Das ich mir hätte einen Schritt sparen können und gleich hätte so schreiben können:
 f dx^3 - \int z g^{\star} p_y f dx^3 = \int (y p_z g)^{\star} f dx^3 - \int (z p_y g)^{\star} f dx^3 ) ? ?
| index_razor hat Folgendes geschrieben: |
Noch ein paar Bemerkungen. 1) Es gilt zwar im allgemeinen nur ^t=B^tA^t) und somit für hermitesche Operatoren und somit für hermitesche Operatoren ^t=BA) . Sofern aber . Sofern aber  und und 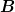 vertauschen, gilt die Beziehung, die du verwenden wolltest: vertauschen, gilt die Beziehung, die du verwenden wolltest: ^t=AB) . Der Grund für die Hermitezität der Drehimpulsoperatoren ist also, daß Ort und Impuls in verschiedene Raumrichtungen vertauschen. . Der Grund für die Hermitezität der Drehimpulsoperatoren ist also, daß Ort und Impuls in verschiedene Raumrichtungen vertauschen.
2) Du hast an keiner Stelle direkt benutzt, daß
 f(x)\dd x)
ein Integral über den Ortsraum ist. Die einzigen Eigenschaftem, die du benötigst, sind die Linearität in 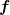 , d.h , d.h

für alle Konstanten  und alle Funktionen und alle Funktionen  , sowie , sowie
 . .
Vielleicht hast du ja Lust und Neigung, denselben Beweis nochmal allein unter Ausnutzung dieser rein abstrakten Eigenschaften des Hilbertraum-Produkts zu führen ohne Bezug auf irrelevante Details der speziellen Ortsdarstellung in einem Funktionenraum. Lehrreich könnte es jedenfalls sein. |
zu 1.) Ja stimmt. Danke für die Anmerkung.
zu 2.) Also ich habe den einen Beweis schon über die eine Methode gemacht. Du hast jetzt noch eine zweite Variation aufgeschrieben mittelns Linearität... In meinem Skript lautet diese Möglichkeit etwas anders, aber ich denke, der Verfasser des Skripts möchte aufs gleiche hinaus:
* Ein Operator  ist linear, falls ist linear, falls 
* Ein Operaor  heißt hermitesch, falls er linear ist und falls heißt hermitesch, falls er linear ist und falls 
Ist das das was du meinst? |
|
 |
| index_razor |
 Verfasst am: 19. Aug 2016 19:46 Titel: Verfasst am: 19. Aug 2016 19:46 Titel: |
|
| jojo22 hat Folgendes geschrieben: | zur Vervollständigung ich versuche noch die Hermitizität von  zu zeigen: zu zeigen:
[...]
und ab hier geht der Beweis wie für Hermitizität de Impulsoperators... also partielle Integration, nur man hat halt dx^3 anstelle dx, aber man muss eh nur nach einer Dimension integrieren.
^{\star} f dx^3 - \int (z p_y g)^{\star} f dx^3 = \int ((y p_z - z p_y) g)^{\star} f dx^3 )
|
Ab hier hast du benutzt, daß 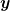 und und  , etc. vertauschen. Und mehr als diese algebraischen Eigenschaften benötigst du auch nicht. Indem du alle Operatoren explizit in der Ortsdarstellung aufschreibst, machst du den Beweis nur komplizierter als er eigentlich sein müßte. , etc. vertauschen. Und mehr als diese algebraischen Eigenschaften benötigst du auch nicht. Indem du alle Operatoren explizit in der Ortsdarstellung aufschreibst, machst du den Beweis nur komplizierter als er eigentlich sein müßte. |
|
 |
| index_razor |
 Verfasst am: 19. Aug 2016 19:36 Titel: Verfasst am: 19. Aug 2016 19:36 Titel: |
|
| jojo22 hat Folgendes geschrieben: |
sieht das gut aus? |
Ja.
Noch ein paar Bemerkungen. 1) Es gilt zwar im allgemeinen nur ^t=B^tA^t) und somit für hermitesche Operatoren und somit für hermitesche Operatoren ^t=BA) . Sofern aber . Sofern aber  und und 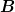 vertauschen, gilt die Beziehung, die du verwenden wolltest: vertauschen, gilt die Beziehung, die du verwenden wolltest: ^t=AB) . Der Grund für die Hermitezität der Drehimpulsoperatoren ist also, daß Ort und Impuls in verschiedene Raumrichtungen vertauschen. . Der Grund für die Hermitezität der Drehimpulsoperatoren ist also, daß Ort und Impuls in verschiedene Raumrichtungen vertauschen.
2) Du hast an keiner Stelle direkt benutzt, daß
 f(x)\dd x)
ein Integral über den Ortsraum ist. Die einzigen Eigenschaftem, die du benötigst, sind die Linearität in 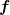 , d.h , d.h

für alle Konstanten  und alle Funktionen und alle Funktionen  , sowie , sowie
 . .
Vielleicht hast du ja Lust und Neigung, denselben Beweis nochmal allein unter Ausnutzung dieser rein abstrakten Eigenschaften des Hilbertraum-Produkts zu führen ohne Bezug auf irrelevante Details der speziellen Ortsdarstellung in einem Funktionenraum. Lehrreich könnte es jedenfalls sein. |
|
 |
| jojo22 |
 Verfasst am: 19. Aug 2016 19:01 Titel: Verfasst am: 19. Aug 2016 19:01 Titel: |
|
zur Vervollständigung ich versuche noch die Hermitizität von  zu zeigen: zu zeigen:
 f dx^3 = \int g^{\star} (yp_z) f dx^3 - \int g^{\star} zp_y f dx^3 = \\ \int y g^{\star} (p_z) f dx^3 - \int z g^{\star} p_y f dx^3 = \frac{\hbar}{i} \int y g^{\star} \frac{\partial }{\partial z} f dx^3 - \frac{\hbar}{i} \int z g^{\star}\frac{\partial }{\partial y} f dx^3 )
und ab hier geht der Beweis wie für Hermitizität de Impulsoperators... also partielle Integration, nur man hat halt dx^3 anstelle dx, aber man muss eh nur nach einer Dimension integrieren.
^{\star} f dx^3 - \int (z p_y g)^{\star} f dx^3 = \int ((y p_z - z p_y) g)^{\star} f dx^3 = \int (l_x g)^{\star} f dx^3 )
Also... qed...? Vielen Dank |
|
 |
| jojo22 |
 Verfasst am: 19. Aug 2016 18:32 Titel: Verfasst am: 19. Aug 2016 18:32 Titel: |
|
| index_razor hat Folgendes geschrieben: | | jojo22 hat Folgendes geschrieben: |
Gilt allgemein:  sind die hermitesch konjugierten, bzw. hermiteschen Operatoren von A und B. Daraus folgt: sind die hermitesch konjugierten, bzw. hermiteschen Operatoren von A und B. Daraus folgt:  und und  sind die hermitesch konjugierten, bzw. hermiteschen Operatoren zu "A+B" und "A*B"? sind die hermitesch konjugierten, bzw. hermiteschen Operatoren zu "A+B" und "A*B"?
|
Nein, für das Produkt gilt das nicht (sondern ^t=B^tA^t) ), aber du benötigst diese Aussage auch nicht. Benutze einfach ), aber du benötigst diese Aussage auch nicht. Benutze einfach 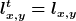 . Versuchs mal mit der Linearität von . Versuchs mal mit der Linearität von  , also so , also so
\dd x = \int g^\star(l_x f)\dd x \pm i\int g^\star(l_y f)\dd x = ...) |
ok. also:
\dd x = \int g^\star(l_x f)\dd x \pm i\int g^\star(l_y f)\dd x = \int (l_x g^\star) f\dd x \pm i\int (l_y g^\star) f\dd x = \int (l_x g^\star) f\dd x \pm \int (il_y g^\star) f\dd x = ) ^\star f\dd x \mp \int (il_y g)^\star f\dd x = \int (l_{\mp} g)^\star f\dd x = \int (A^t f)^* g dx^3 )
sieht das gut aus? |
|
 |
| index_razor |
 Verfasst am: 19. Aug 2016 17:22 Titel: Verfasst am: 19. Aug 2016 17:22 Titel: |
|
| jojo22 hat Folgendes geschrieben: |
Gilt allgemein:  sind die hermitesch konjugierten, bzw. hermiteschen Operatoren von A und B. Daraus folgt: sind die hermitesch konjugierten, bzw. hermiteschen Operatoren von A und B. Daraus folgt:  und und  sind die hermitesch konjugierten, bzw. hermiteschen Operatoren zu "A+B" und "A*B"? sind die hermitesch konjugierten, bzw. hermiteschen Operatoren zu "A+B" und "A*B"?
|
Nein, für das Produkt gilt das nicht (sondern ^t=B^tA^t) ), aber du benötigst diese Aussage auch nicht. Benutze einfach ), aber du benötigst diese Aussage auch nicht. Benutze einfach 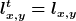 . Versuchs mal mit der Linearität von . Versuchs mal mit der Linearität von  , also so , also so
\dd x = \int g^\star(l_x f)\dd x \pm i\int g^\star(l_y f)\dd x = ...) |
|
 |
| jojo22 |
 Verfasst am: 19. Aug 2016 16:53 Titel: Verfasst am: 19. Aug 2016 16:53 Titel: |
|
| jh8979 hat Folgendes geschrieben: | Also fehlt Dir eigentlich die komplette Aufgabe...
Wenn Du das in Ortsdarstellung hinschreibst, dann solltest Du Deinen Operator auch in Ortsdarstellung benutzen (und die korrekte Definition für l+- einsetzen...). |
ich schreib es nochmal ausführlicher hin, was ich denke "zu haben". :-)
| index_razor hat Folgendes geschrieben: | Die Definition der Leiteroperatoren (geht es um die Drehimpulsalgebra?) lautet  . In deiner Definition fehlt also die imaginäre Einheit. Wenn du die korrekte Definition mit der Hermitezität der Drehimpulsoperatoren . In deiner Definition fehlt also die imaginäre Einheit. Wenn du die korrekte Definition mit der Hermitezität der Drehimpulsoperatoren  verbindest, solltest du die Behauptung beweisen können. verbindest, solltest du die Behauptung beweisen können. |
Ja es geht um Dreimpulsalgebra. Im Skript und auch sonst wo haben wir eigentlich ein großes "L" immer benutzt, aber ich wüsste nicht was das klein "l" sonst sein soll. Außerdem sind wir gerade bei diesem Thema. Ja ich habe das "i" vergessen, habs korrigiert :-)
Wie oben beschrieben soll ^* g dx^3 ) sein, wobei sein, wobei  und und  . Ich beginne mit der linken Seite der "Istgleichs": . Ich beginne mit der linken Seite der "Istgleichs":
 dx^3 = \int_{-\infty}^{\infty} f^* ((l_x \pm il_y) g) dx^3 = \int_{-\infty}^{\infty} f^* ((y p_z - z p_y \pm i (z p_x - x p_z ) g) dx^3 ) . Jetzt weiß ich, dass x, y, z hermitesch sind. Ebenso wie die Impulsoperatoren. Oder wie du, index_razor geschrieben hast: Die Drehimpulsoperatoren sind hermitesch. (Drehimpulsoperatoren bestehen ja aus x, y, z und den Impulsoperatoren) . Jetzt weiß ich, dass x, y, z hermitesch sind. Ebenso wie die Impulsoperatoren. Oder wie du, index_razor geschrieben hast: Die Drehimpulsoperatoren sind hermitesch. (Drehimpulsoperatoren bestehen ja aus x, y, z und den Impulsoperatoren)
Ist allgemein die Summe und das Produkt hermitescher, bzw hermitesch konjugierter Operatoren auch hermitesch bzw hermitesch konjugiert?
Gilt allgemein:  sind die hermitesch konjugierten, bzw. hermiteschen Operatoren von A und B. Daraus folgt: sind die hermitesch konjugierten, bzw. hermiteschen Operatoren von A und B. Daraus folgt:  und und  sind die hermitesch konjugierten, bzw. hermiteschen Operatoren zu "A+B" und "A*B"? sind die hermitesch konjugierten, bzw. hermiteschen Operatoren zu "A+B" und "A*B"?
Falls ja, kann ich weiterrechnen:
) f^* ) g dx^3 = \\ \int_{-\infty}^{\infty} ((l_x \pm i l_y) f^*) g dx^3 = \int_{-\infty}^{\infty} ((l_x \mp i l_y) f)^* g dx^3 = \int_{-\infty}^{\infty} (l_{\mp} f)^* g dx^3 \\ = \int_{-\infty}^{\infty} (A^t f)^* g dx^3 )
ist das der Beweis?
Danke |
|
 |
| index_razor |
 Verfasst am: 19. Aug 2016 15:26 Titel: Verfasst am: 19. Aug 2016 15:26 Titel: |
|
Die Definition der Leiteroperatoren (geht es um die Drehimpulsalgebra?) lautet  . In deiner Definition fehlt also die imaginäre Einheit. Wenn du die korrekte Definition mit der Hermitezität der Drehimpulsoperatoren . In deiner Definition fehlt also die imaginäre Einheit. Wenn du die korrekte Definition mit der Hermitezität der Drehimpulsoperatoren  verbindest, solltest du die Behauptung beweisen können. verbindest, solltest du die Behauptung beweisen können. |
|
 |
| jh8979 |
 Verfasst am: 19. Aug 2016 15:23 Titel: Verfasst am: 19. Aug 2016 15:23 Titel: |
|
Also fehlt Dir eigentlich die komplette Aufgabe...
Wenn Du das in Ortsdarstellung hinschreibst, dann solltest Du Deinen Operator auch in Ortsdarstellung benutzen (und die korrekte Definition für l+- einsetzen...). |
|
 |
| jojo22 |
 Verfasst am: 19. Aug 2016 14:34 Titel: Hermitesch konjugierter Leiteroperator Verfasst am: 19. Aug 2016 14:34 Titel: Hermitesch konjugierter Leiteroperator |
|
hallo :-)
Ich soll beweisen, dass der Leiteroperator 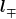 das hermitesch konjugierte zu das hermitesch konjugierte zu  ist. ist.
Allgemein: ^* g dx )
Wenn ich dies nun rechne mit  und und 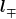 dann fehlt mir der Zwischenschritt, wie ich von dann fehlt mir der Zwischenschritt, wie ich von
 g dx^3 )
zu
f^*) g dx^3 )
komme.
Hat jemand eine Idee? danke  |
|
 |




