Okay, cool. Ist ja echt sehr trivial. Haste recht, Danke.  |
|
| Ich mache das nur, weil ich das einfache Hinschreiben der Trf. mittels von U für zu trivial hielt; ich habe eben eine explizite Form von U in einer Basis bestimmten gewählt und die Trf. explizit berechnet. | |
| Ja, jetzt hast du es in einer anderen Basis ausgedrueckt. Aber ich sehe jetzt nicht wirklich den Grund warum du das machst. Kannst du das vll. noch bisschen erlaeutern, oder ist das nur aus aesthetischen Gruenden? |
|
Prima; jetzt setzen wir mal ein: Diesen Zusammenhang habe ich gemeint |
|||
| Ich hab nochmals nachgefragt und es war einfach gefragt wie sich die Dichtematrix transformiert, falls Also ist folgendes korrekt: Danke fuer die Hilfe.  Ich komme auf euch/dich zurueck  |
|
| Frag doch nochmal nach, was erwartet wird | |
| Leider ist das die gesamte Aufgabenstellung. Aber die Dichtematrix beinhaltet doch immer die Psis: http://de.wikipedia.org/wiki/Dichtematrix#Konstruktion Ja die Psi's sind nicht orthogonal. Das sind ja die verschiedenen Zustaende aus dem Ensemble. |
|
| Man kann ja eine entsprechende unitäre Basistransformation durchführen; die beiden Transformationen entsprechen einander. Ich glaube aber, dass in der Aufgabe etwas anderes erwartet wird; insbs. ist mir die Rolle der psi-Darstellung noch nicht klar; das scheint i.A. keine Orthonormaldarstellung zu sein, daher ist die Argumentation etwas schwieriger. Ist das wirklcih die gesamte Aufgabenstellung? |
|
| Jetzt hast du ja Rho in einer anderen Basis ausgedrueckt und was meinst und wo ist jetzt die Unitaeretransformation geblieben? Ich verstehe noch nicht ganz warum du das machst. Danke schon mal fuer deine grosse Hilfe 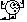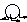 |
|
| Ich drücke es einfach in irgendeiner Basis aus | |
| Und wo hast du jetzt die Unitaere Transformation? Oder kommt die dann noch drauf? Warum willst du es in der |k> - Basis ausdruecken? |
|
| So hätte ich das auch angesetzt, aber das ist evtl. etwas zu trivial. Wie wär's mit |
|
| Die alte Dichtematrix war: Nun fuer ich die Transformation durch: Daher folgt: Stimmt das so? Oder ist dann einfach gefragt: Also dass ich dann einfach |
|
| Ich denke, es geht um eine Basistransformation Wie lautet dann die neue Dichtematrix bzgl. der neuen Basis? |
|
| Also ich hab jetzt: Jetzt ueberpreufe ich noch deine Bedingung: Das passt also. Danke Jungs. Bei der b) komme ich gerade auch nicht weiter, vll. koennt ihr mir da noch nen Tipp geben: (b) Find the density operator Ich versteh gar nicht was damit gemeint ist, denn es is ja bekannt, dass fuer alle Dichtematrizen gilt: Oder versteht ihr was damit gemeint ist? |
|
| Die Summe kollabiert zu einem einzigen Term, denn Aber die Summe über k kannst du zuletzt noch als Probe berechnen; du hast als Wahrscheinlichkeit, und dafür muss gelten Das kannst du noch nachprüfen. |
|
| Nicht ueber k summieren, dann passt es und du hast P_k. | |
| Danke fuer die Hilfe. Ich frag morgen nochmals den Prof. Ich komme dann auf: Kannst du das bestaetigen? |
|
| Ich finde die Tatsache, dass in den verschiedenen Zuständen jeweils k verwendet wird reichlich seltsam. Deshalb meine Schreibweise und mein Ansatz (ich hoffe, ich interpretiere da nichts falsch) Gegegeben ist ein Dichteoperator Gesucht ist die Wahrscheinlichkeit q(k), das System in einem Zustand einer anderen Orthonormalbasis zu finden. Mein Ansatz wäre, den Erwartungswert des Projektors zu berechnen: Die Spur berechnet man am besten über dieselbe Orthonormalbasis |k>. Dabei reduziert sich die Spursumme wg. Orthonormiertheit auf den k-ten Basisvektor. |
|
| Ok ich schreibs mal (ist auf Englisch) : We consider mixed state which is a statistical mixture of pure states. Desnity operator is defined as: where the pure states Find the probability that measurement in the orthogonal basis |
|
| Kannst du die Aufgabe im Orginal reinstellen? | |
| Jap, so ist die Aufgabe denk gemeint. Jedoch sind alle Indices so gwaehlt wie ich im ersten Post. Macht die Aufgabe so Sinn? |
|
| Verstehe ich dich richtig: Gegegeben ist ein Dichteoperator Gesucht ist die Wahrscheinlichkeit q(k), das System in einem Zustand einer anderen Orthonormalbasis zu finden? |
|
| Hi Leute, hab ne Frage: Gegeben sei die Dichtematrix: Weiterhin seien die Zustaende normiert und Nun gilt es die Wahrscheinlichtkeit zu finden, dass das Ergebnis Ich hoffe die Aufgabe ist verstaendliche formuliert. Ich habe leider gar keine Ahnung was ich machen soll, kann mir vll. jemand einen Tipp geben. Viele Gruesse und schon mal Danke fuer Helfen, eva |
|