| Autor |
Nachricht |
Jochen123
Anmeldungsdatum: 03.09.2006
Beiträge: 5
|
 Jochen123 Verfasst am: 05. Sep 2007 21:27 Titel: Buch zur Herleitung des Wasserstoffatom |
 |
|
Hallo zusammen,
wir haben jetzt bereits zwei mal das Wasserstoffatom disskutiert, und ich sage mal es war vermutlich die Standardherleitung, sprich zuerst die Asymptotik abhandeln und dann mittels Potenzreihenansatz die DGL gelöst. Doch die Profs hatten auf Nachfragen immer keine Antworten (z.B. beim Potenzreihenansatz kommt man auf eine Rekursionsbeziehung für die Koeffizienten. Das Problem ist nur, dass es eine DGL zweiter Ordnung ist, man jedoch nur einen freien Parameter hat) Oder warum ist denn die Lösung eindeutig, wenn sie das denn überhaupt ist.
Weiß jemand ein gutes Buch über Quantenmechanik, wo die physikalischen Probleme mit mathematische Präzission diskutiert werden? Bei den mir bekannten Physikbüchern bleiben die mathematische Probleme meistens auf der Strecke.
Danke.
P.S. Gibt vll was passendes aus dem Bereich der mathematischen Physik |
|
 |
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 06. Sep 2007 08:40 Titel: Re: Buch zur Herleitung des Wasserstoffatom |
|
|
| Jochen123 hat Folgendes geschrieben: |
Weiß jemand ein gutes Buch über Quantenmechanik, wo die physikalischen Probleme mit mathematische Präzission diskutiert werden? Bei den mir bekannten Physikbüchern bleiben die mathematische Probleme meistens auf der Strecke. |
http://www.physik.uni-bielefeld.de/~schmid/Lehre/QM_WS02/qm1total.pdf
Hier erfolgt im Kapitel 2.3 eine ziemlich ausführliche Behandlung.
Es zahlt sich eigentlich nicht aus ein Buch zu kaufen, da es dutzende pdf Vorlesungsunterlagen auf sehr hohem Niveau gibt.
Zur Eindeutigkeit:
Die Lösung ist nur bis auf die Wahl der Hauptqunatenzahl n, der Drehimpulsquantenzahl l < n und der z-Komponente des Drehimpulses m (2l+1 Ausrichtungen) eindeutig. l und m werden durch die Kugelflächenfunktionen abgedeckt.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Jochen123
Anmeldungsdatum: 03.09.2006
Beiträge: 5
|
| Jochen123 Verfasst am: 06. Sep 2007 14:06 Titel: |
|
|
Danke erstmal für den Link, doch klarer wird es trotzdem nicht, denn betrachte z.B. mal Kapitel 2.3.4:
Die Schröderingergleichung wird reskaliert, kein Thema. Dann macht man asymptotische Betrachtungen, kann ich noch akzeptieren, wenn man auch zu diesem Zeitpunkt noch nicht weiß, dass die Lösung überhaupt so lange existiert (vgl. =0) , hat ) als Lösung und existiert nur auf ) )
Dann macht man einen Ansatz und bekommt eine Rekursionsbeziehung. Spätenstens hier muss man hier muss man sich wundern. Die DGL ist eine DGL zweiter (!!!!) Ordnung und man hat einen (!!!) freien Wahlparameter, nämlich 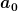 . Sprich, hier muss etwas schief gegangen sein. Schaut man sich die DGL genauer an, reduziert die Ordnung, so sieht man, dass die DGL in der Null singulär ist und somit der Satz von Picard-Lindelöf nicht anwendbar ist. Sprich, ich habe zwar eine Lösung, kann aber keine Aussage treffen, ob es die einzige ist.
Doch das wird auch in dem Skript verschwiegen.
Ich hoffe ich konnte mein Problem an diesem Beispiel erklären. Vll kann auch jemand mir erstmal erklären wie man zeigt, dass es keine weiteren Lösungen gibt. |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 06. Sep 2007 18:36 Titel: |
|
|
Ich verstehe hier zwar viel zuwenig (eigentlich gar nichts...) von der Theorie der Differentialgleichungen, aber grundsätzlich sind hier zwei Lösungen möglich:
 = \rho^{l+1}e^{-\rho/2} p(\rho))
und
 = \rho^{l+1}e^{+\rho/2} q(\rho))
von denen allerdings die zweite nicht verwendet werden darf, da sie zu unphysikalischem Verhalten im Unendlichen führen würde. Wäre das betrachtete Intervall nur endlich, so wäre die allgemeine Lösung zunächst eine beliebige Überlagerung beider Komponenten. Die genaue Art der Überlagerung wird durch Randbedingungen festgelegt. In unserem Fall ist die Überlagerung eben so, dass der Anteil der zweiten Komponente verschwindet. Das kommt in der Physik sehr oft vor: Z.B. gibt es oft grundsätzlich cos- und sin-Schwingungen als Lösung, wo allerdings wegen spezieller Randbedingungen (Knoten oder Bäuche an bestimmten Stellen) eine Lösungsart ausfällt (zB. Orgelpfeife). Schliesslich kann es immer nur eine physikalische Lösung geben. Hier ist die Randbedimgung eben die Bedingung, dass man im Unendlichen vom Atom nichts mehr spüren darf, was für mich mathematisch ausreichend erscheint.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Jochen123
Anmeldungsdatum: 03.09.2006
Beiträge: 5
|
| Jochen123 Verfasst am: 06. Sep 2007 21:55 Titel: |
|
|
Sorry, aber ich glaube so einfach geht das nicht. Du hast die DGL
}{\rho^2}+ \frac \nu \rho - \frac 1 4 \right)u_l(\rho)=0)
und entscheidest dich für den Ansatz
=\rho^{l+1}e^{-\frac \rho 2}p(\rho))
und bekommst nun eine neue DGL
 + (2l + 2 - \rho)p'(\rho)+(\nu-l+1)p(\rho)=0)
die du jetzt unabhängig von den Überlegungen vorher durch einen Potenzreihenansatz lösen willst. Dabei kommst du auf die Rekursionsbeziehung
(k+2l +2)}a_k)
Und hier tritt jetzt das Problem der fehlenden zweiten Konstanten auf!!! |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 07. Sep 2007 09:30 Titel: |
|
|
| Jochen123 hat Folgendes geschrieben: | | Sorry, aber ich glaube so einfach geht das nicht. |
Ja, da hast du natürlich recht. Das hab ich in der Eile übersehen. 
Antwort hab ich darauf nun keine, aber nur einen sehr sehr vagen Verdacht ohne Tiefgang, den ich hier mal - ohne zu wissen, ob ich Unsinn rede - zu formulieren versuche:
Wenn man den Ansatz
hernimmt, und voraussetzt, dass sich p(x) an der Stelle 0 in eine Potenzreihe entwickeln lässt, so ist p(x) eben bis auf einen Faktor gegeben und man hat keinen Freiraum für weitere Funktionen dieser Art. Möglicherweise gibt es aber Lösungsfunktionen von p, die sich bei x=0 eben nicht in eine Potenzreihe entwickeln lassen. Das wäre dann eine bei x=0 - sagen wir mal - "zickige" Funktion mit irgendeiner Singularität. Da wir aber voraussetzen, dass u(0) = 0 sein soll, darf p nicht stärker gegen unendlich gehen als
 \propto \frac{1}{x^{l+1}})
womit ich mal (nur aus dem Bauch heraus) schliesse, dass es sich um eine hebbare Unstetigkeit handeln muss, was wiederum dazu führt, dass man (das nunmehr "benigne") p(x) in eine Laurentreihe entwickeln kann. Für diese gilt aber wiederum die gleiche Rekursionsformel (ich hoffe das stimmt...), und man sieht dann auch sofort , dass wegen des Faktors (k+1) im Nenner alle Koeffizienten a(k) für k<0 verschwinden müssten. Damit wäre man wieder bei der originalen Entwicklung. Es könnte also durchaus eine weitere Lösung existieren, diese würde aber unsere Bedingung u(0)=0 verletzen, wäre bei x=0 hochgradig singulär (sozusagen "pervers" wie unser Prof immer zu sagen pflegte) und somit nicht relevant.
Ich weiss, sehr "physikerhaft" formuliert, wenn du was besseres rausfindest, lass es uns bitte wissen, da es mich nun auch irgendwie interessiert. Schon im Matheboard nachgefragt? Dort gibt es sehr gute Mathematiker (die ich aber leider oft nicht mehr verstehe  ).
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Jochen123
Anmeldungsdatum: 03.09.2006
Beiträge: 5
|
| Jochen123 Verfasst am: 07. Sep 2007 16:57 Titel: |
|
|
wenn ich mich richtig an die DGL-Vorlesung erinnere, dann reicht es p als Potenzreihe zu betrachten und kann sich die Laurentreihe sparen.
(Nur so als Anmerkung: Es gibt unendlich oft diff'bare Funktionen, die sich nicht überall in eine Taylorreihe entwickeln lassen, zb. e^{1/x^2}, sprich es muss gar keine Singularität vorliegen)
Nee, so kommt man da nicht weiter, denn die Theorie der gew. DGL greift meiner Meinung nach bei der zweiten DGL eben nicht und man somit so zusagen aufgeschmissen ist.
Ich werde mal bei den Mathematikern nachfragen, vll ergibt sich hier noch was.
Oder vll ließt hier ja noch jemand mit, der viel Ahnung von DGLen hat. |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 07. Sep 2007 18:39 Titel: |
|
|
| Jochen123 hat Folgendes geschrieben: | wenn ich mich richtig an die DGL-Vorlesung erinnere, dann reicht es p als Potenzreihe zu betrachten und kann sich die Laurentreihe sparen.
(Nur so als Anmerkung: Es gibt unendlich oft diff'bare Funktionen, die sich nicht überall in eine Taylorreihe entwickeln lassen, zb. e^{1/x^2}, sprich es muss gar keine Singularität vorliegen)
|
Versteh ich nun nicht. Meiner Meinung ist das sogar eine wesentliche Singularität. Trotzdem kann ich das nach einer Laurentreihe entwickeln, oder ? .
Ich hab auch nicht behauptet, dass es eine weitere Lösung geben kann oder nicht, sondern nur zu zeigen versucht, dass eine weitere Lösung unphysikalisch wäre, da eine physikalisch akzeptable Lösung (zumindest in einer Umgebung von 0) in eine Laurentreie entwickelbar sein muss, und diese aufgrund der Rekursionsformel keine Koeffizienten mit n<0 haben kann.
Ich werd mal verfolgen was sich bei den Kollegen tut !
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 12. Sep 2007 22:02 Titel: |
|
|
@Jochen123: Gibt es da jetzt schon eine Lösung dafür ?
Ich hab einiges an "Nachdenken" investiert und bin deshalb schon sehr neugierig. Im Matheboard steht nichts, oder? Kannst du dort evtl. mal nachfragen, da ich von DGL keine Ahnung habe und die Frage gar nicht zu stellen in der Lage wäre.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
